Síntesis (7): fundamentos de síntesis sustractiva (II)
¿Oscilador o pedorreta? La necesidad de los filtros
[Índice]La anterior entrega estuvo centrada en los osciladores y sus formas de onda más habituales, pero tal como vimos y escuchamos allí, suenan por sí mismos muy hirientes, en una forma que yo intentaba reflejar con el término ‘zumbador’. Vamos a comenzar hoy haciendo pedorretas (en serio). Pensad en ¿cómo producimos las ‘pedorretas’?
Para ellas no usamos las cuerdas vocales como elemento ‘excitador’ o productor de la vibración. Las cuerdas están muy ‘dentro’ y sólo podemos oírlas modificadas tras su paso por todos los tubos y cavidades que ha de atravesar hasta llegar a la boca y salir al exterior. Cualquier sonido producido en las cuerdas vocales (nuestro oscilador habitual) viene ‘filtrado’ cuando lo escuchamos salir de nuestra boca. El resultado final audible ha perdido en ese camino su ‘fiereza’ original.
Pero tenemos la posibilidad de escuchar algo parecido al sonido de las cuerdas vocales haciendo pedorretas. Para generarlas usáis la boca sólo para insuflar una corriente de aire por una pequeña abertura entre los dos labios y con la mano ayudáis a retener los labios en su sitio. Estáis imitando lo que hace un trompetista que pega sus labios a la embocadura. La presión del aire crece y en un momento es tal que fuerza los labios a separarse. Al separarse sale un exabrupto de aire, se libera la presión, los labios pueden volver a cerrarse y comienza el ciclo. Y cada ciclo está definido por ese exabrupto, ese aire que sale con máxima fuerza durante un instante y es sucedido por el silencio de los labios cerrados mientras la presión vuelve a crecer por detrás de ellos.
Un modelo por tanto para la síntesis de la pedorreta es usar tal cual un oscilador de pulsos estrechos (como representación de ese estallido de aire que se repite periódicamente, aunque haría falta sumarle algo de ruido para imitar el soplido que también escapa). Dicho en términos que ya vamos conociendo: un oscilador rectangular con una anchura de pulso ajustada para pulsos estrechos. La pedorreta es el sonido propio de nuestros tan amados osciladores… y pocos temas conoceréis (al menos que hayan dejado cierta memoria en la historia musical o que hayan dejado sustancioso metal en el bolsillo de sus autores) que se hayan compuesto para pedorretas y sección rítmica (hay alguno, pero excepcional).
Los sonidos de los vientos metal son pedorretas hábilmente modificadas al tener que atravesar el tubo que forma el cuerpo del instrumento (y nadie negará que suenan variados y deliciosos, con infinidad de matices y articulaciones).
Si fuéramos capaces de oír la vibración natural y libre de nuestras cuerdas vocales, sería de nuevo una pedorreta (y sin embargo a partir de ellas somos capaces de producir gran variedad de sonidos amables y cálidos con la voz).
El sonido de los dientes de sierra hace honor a su nombre y no es menos incisivo que el que producen los trenes de pulsos. La presencia de transiciones abruptas en la forma de onda, de esos ‘precipicios’ o ‘saltos’ que podemos ver en los pulsos y dientes de sierra es el origen de un brillo antinatural, excesivo, a menudo molesto si lo oímos tal cual.
La conclusión a la que pretendo llegar con todo lo anterior es que el mérito puede estar por tanto más en el arte de modificar que en el de disponer de una fuente inicial magnífica. Bienvenidos al mundo de los filtros, los responsables de que a partir de esa ‘fiereza’ de los osciladores típicos en el mundo sustractivo obtengamos toda una amplia variedad de sonoridades. Y no me interpretéis mal: claro que los osciladores son importantes, pero hoy nuestro protagonista es el filtro.
Para presentar el tipo de gráficos y vídeos que vamos a usar hoy, os muestro y comento este primero.
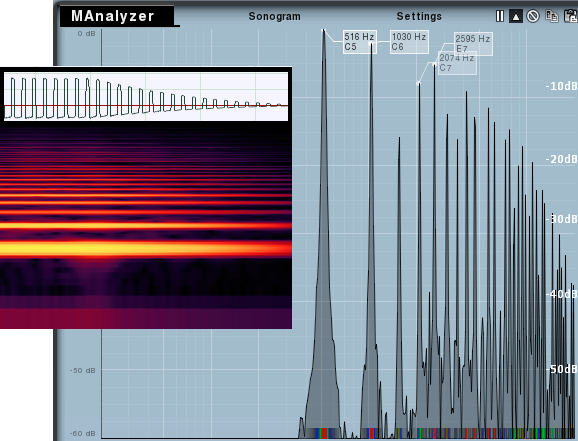
Veis en el recuadro una forma de onda (claramente un pulso no cuadrado sino rectangular, con una anchura que no es 50%), y sobre fondo negro veis el correspondiente espectrograma (en el que identificáis con facilidad esas líneas ‘calientes’ horizontales que corresponden con el desarrollo de los diferentes armónicos a lo largo del tiempo), y finalmente en la figura grande de fondo encontráis el espectro correspondiente a un momento concreto de esa señal, en el que podéis ver los principales armónicos y su nivel, etc.
La señal está generada con iMS-20 para iPad. El espectrograma ha sido obtenido con Audition de Adobe y la gráfica grande haciendo uso de MAnalizer (plug-in gratuito, de Melda). Las rayas no son ‘puras’ porque, como veis en la forma de onda, hay una envolvente rápidamente decreciente y eso implica que no son tonos ‘puros’. Como se está usando una escala de frecuencia logarítmica (en vez de lineal) las rayas armónicas aparecen más separadas en bajas que en altas frecuencias (en una escala lineal estarían equiespaciadas).
Filtros al rescate
[Índice]La definición de filtro en ingeniería lleva a hablar de un ‘sistema lineal e invariante’. Pero lo que nos interesa a nuestros propósitos no es su definición, sino su acción: con un filtro podemos modificar selectivamente unas componentes de frecuencia frente a otras (en nivel y en fase).
Como estamos de momento con una presentación muy general sobre la síntesis sustractiva, dejemos de lado la modificación en fase (que a menudo se intenta minimizar o equilibrar en los diseños de filtros habituales) y centrémonos en la modificación sobre el nivel, que es la función principal de los filtros usados en sintetizadores (sobre la fase podéis leer otro par de artículos que escribí en febrero de 2013: www.hispasonic.com/pablofcid/articulos).
De lo que estamos hablando es de que un filtro nos permite ‘destacar o rebajar’ la presencia de unas regiones u otras de frecuencia. Algo así como un ecualizador (en el fondo otro tipo de filtro) pero con una actuación que en los filtros para síntesis es más ‘quirúrgica’, no sólo ‘cosmética’.
Hay muchos tipos de filtro. En sintetizadores solemos encontrar filtros paso bajo (low pass filter, LPF), paso alto (hish pass filter, HPF), paso banda (band pass filter, BPF) y de eliminación de banda (band reject filter, BRF), pero también hay filtros de formantes (formant filter), de pico (peak), de 'muesca' (notch), en peine (comb), y un largo etc. (por no hablar de las diferencias entre si la implementación del filtro sigue una u otra tecnología y metodología de diseño). De esas complicaciones habrá tiempo de hablar. Hoy nos centraremos en un filtro paso bajo ‘genérico’.
Es el paso bajo el filtro más usado en los sintes, y así cuando sólo existe un único filtro (como en el Korg MS-10 que estamos tomando como excusa en esta parte de la serie -y en tantísimos otros sintetizadores-) será paso bajo. Sólo en sintes algo más generosos en posibilidades podremos encontrar otros tipos de filtro además del paso bajo que siempre está presente.
La acción de un filtro la representamos mediante su respuesta en frecuencia: la ganancia con la que afecta a cada frecuencia puede representarse gráficamente y da una idea muy significativa de cómo actúa (hasta qué punto deja pasar o bloquea ciertas de ellas).
Filtros: la frecuencia de corte
[Índice]Pongamos por caso que la salida de un oscilador (una señal rica en armónicos) atraviesa un filtro paso bajo. Este tipo de filtro deja pasar (sin modificación especial) las componentes cuyas frecuencias quedan por debajo de una determinada frecuencia (llamada frecuencia de corte), pero las que están por encima las somete a una rebaja de nivel apreciable.
El resultado es por tanto un sonido más opaco, con pérdida del contenido de alta frecuencia (que en las salidas de los osciladores ‘en bruto’ suele ser excesivo).
La siguiente gráfica correspondería a nuestro MS-10 que usamos como leit-motiv (en realidad estoy usando un iMS-20, como sabéis, pero imitando un MS-10). He usado el generador de ruido blanco (en teoría de nivel básicamente constante para todas las frecuencias) para atacar el filtro (paso bajo), con un ajuste de frecuencia de corte allá por los 2 o 3 KHz. Al ser un ruido no identificamos unas frecuencias principales, parciales o armónicos claros, sino energía repartida por todo el espectro. Podéis ver que, en lugar de un espectro ‘plano’ como esperamos en el ruido, aparece la pérdida progresiva de energía en altas frecuencias por la acción del filtro, e incluso somos capaces de intuir ‘a ojo’ la respuesta en frecuencia del filtro (que he marcado sobre la figura).
Tal como muestran los dibujos y gráficos anteriores, la actuación de un filtro no suele ser ‘sí o no’, ‘pasa o no pasa’, sino que es gradual. Se atenúa el nivel tanto más cuanto más lejos se está de la frecuencia de corte. Los parciales y componentes más altos se atenúan más.
Por debajo de la frecuencia de corte, las componentes espectrales pasan sin verse afectadas, sin cambios. Se trata de la ‘banda de paso’ o de la zona en la que el filtro tiene ganancia unidad (0dB), es decir, ni incrementa ni rebaja, sencillamente deja la señal tal como es.
Comparad esa figura anterior y esta. De nuevo el ruido pero mucho más filtrado, con la frecuencia de corte desplazada muy abajo, hasta los subgraves, hasta tal punto que la señal casi desaparece del todo, no porta apenas energía tras tanto filtrado: la veis minúscula en el recuadro, pero aún así con la ‘huella’ de haber cruzado el filtro.
La definición ‘rigurosa’ de la frecuencia de corte corresponde (es como se ha definido así en la teoría de filtros desde siempre) como el punto en el cual la ganancia ‘unidad’ que existe en la banda de paso cae 3dB. Por tanto, en rigor, la acción de filtrado comienza un poco antes de la frecuencia de corte, pero se ha tomado esa referencia de los -3 dB para definir el punto que llamamos ‘frecuencia de corte’ en toda la teoría y práctica sobre filtros.
Pendiente en los filtros (dB/octava, nº de polos)
[Índice]La mayor o menor pendiente del filtro es una de las características que definen a los filtros y que impactan sobre el tipo de resultado sonoro. Comparad el caso que os muestro en la siguiente figura y el que ilustraba otra anterior semejante.
Mientas con el primero todavía llegaban a aparecer en la salida los parciales 8 y 9, con este último no. Se trata de un filtro más selectivo, con mayor capacidad de discriminación. Y el parámetro que usamos para caracterizar esta cuestión es la ‘pendiente’ del filtro. Un filtro con mayor pendiente es más selectivo, porque la caída progresiva de nivel a partir de la frecuencia de corte es más veloz.
La forma en la que se suele expresar cómo de selectivo es un filtro es mediante la expresión de su pendiente en unidades de dB/octava: cuántos dB (decibelios) menos de ganancia tiene una frecuencia que está por encima de otra una octava (siempre hablando de la zona espectral que se filtra, no de la que se mantiene sin cambios).
Los ecualizadores simples de dos bandas (como los que podemos tener en un piano electrónico o sintetizador como efecto ‘master’ a la salida o los típicos de los amplificadores HiFi) no dejan de ser filtros con frecuencias de corte fijas (paso bajo para el control de graves y paso alto para el de agudos). Lo que hacemos con los controles de ecualización es mezclar en determinadas proporciones las salidas correspondientes a esas franjas del espectro.
En el caso de los filtros presentes en los ecualizadores su pendiente es tan poca (6dB/octava) que no tienen una utilidad real como elemento ‘de síntesis’, sólo quedan para esa ‘ecualización’. No llegan a afectar tanto al sonido como para que podamos apreciar unas diferencias notables de timbre, sólo la coloración propia de la ecualización. Para que ‘se noten’ los filtros tienen que contar con pendiente algo mayor.
Los valores más típicos de pendiente en filtros de sintetizador son 12 dB/octava y 24 dB/octava (mucho más estricto), pero también los hay con 18 (no demasiado frecuentes) o 36 (en filtros ya bastante ‘severos’).
La razón por la que los saltos son de 6 dB/octava sería muy larga de explicar, y obligaría a meternos en las tripas tecnológicas de los sistemas lineales e invariantes. Lo que nos importa es saber que cuanto mayor es la pendiente tanto más selectivo (más ‘estricto’) es el filtro, más ‘abrupta’ es su actuación, más evidente la separación que establece entre las señales que deja pasar y las que elimina.
Otra forma habitual de expresar la pendiente es por el número de polos. El que un filtro pueda ofrecer una mayor o menor pendiente a la postre impacta sobre su complejidad interna. Los filtros en los ecualizadores suelen ser de un único polo y ofrecen 6 dB/oct. Los filtros de 2 polos ofrecen caída de 12dB/octava (por ejemplo el filtro paso bajo de los Korg MS o los Oberheim SEM), los de 3 polos 18 dB/octava (por ejemplo el filtro de la TB-303 BassLine de Roland), los de 4 polos llegan a 24dB/octava (el archiconocido del MiniMoog), y así podríamos seguir (6 polos para 36dB/oct, etc.). El precio de introducir más polos en el diseño es especialmente evidente en la electrónica analógica: se necesitan más componentes, más etapas. Pero sucede igual en el caso digital (requerirá más cómputo un sistema de mayor capacidad de discriminación).
¿Significa eso que un 36dB/oct sea mejor que un 12db/oct? No necesariamente. Lo que sucede es que tienen diferentes ‘colores’. Un filtro de 12dB/oct logra un filtrado que ‘tamiza’, mientras uno de 36dB/oct implica un ‘bloqueo’ de las componentes superiores a la frecuencia de corte. En función de qué tipo de resultado busquemos (imitar tal o cual instrumento, o lograr tal o cual sonoridad) será más adecuado uno u otro.
Lo que sí es cierto es que a menudo los filtros más complejos (los de 24 o 36 dB/oct) pueden configurarse para ‘prescindir’ de alguna de sus etapas y comportarse como filtros de un orden menor. No es extraño que tengamos filtros que podemos ajustar a una u otra pendiente (sencillamente se ‘saltan’ algunas de sus etapas si pedimos un comportamiento de un orden inferior). En ese sentido sí puede ser ‘superior’ un diseño de alto número de polos: porque puede ser más versátil y ‘rebajar’ su comportamiento para imitar a sus hermanos menos dotados. En algunos sintes veréis filtros configurables a 12 o 24 dB/oct mediante algún conmutador que al activarse da o no entrada a una sección del filtro.
A la inversa sería imposible. Un único filtro de 12dB/oct nunca podrá sonar ni configurarse como un 24dB/oct. Es claro: no tiene suficientes ‘polos’ para ello. Pero sí hay una vía: una forma de obtener filtros ‘de orden superior’ es encadenarlos en serie. Aplicar consecutivamente dos filtros de 12dB/octava, combina ambos con el resultado de una caída total de 24 dB/octava. Aunque tiene algunos problemas prácticos, no el menor el de ajustarlos exactamente a la misma frecuencia (que no parece un problema tan grave hasta que pensamos en que esa frecuencia la queremos poder ajustar y mover durante el transcurso de una nota, momento en el cual conseguir que permanezcan bien ‘alineados’ ya no es tan simple).
Hay muchos filtros configurables como paso bajo o paso alto (sin más que modificar un conmutador o un parámetro).
Y no es extraño que ofrezcan un tercer modo de trabajo paso banda. Volvamos a pensar en los filtros de 24 dB/oct (que son muy habituales): el paso a modo ‘paso banda’ hará que presente 12 dB/oct a cada lado puesto que los ‘polos’ se reparten para crear un paso bajo y un paso alto combinados que den lugar al paso banda).
En el caso de la figura, el filtro tiene un comportamiento ‘paso alto’ en torno a fc1 y paso bajo en torno a fc2 y las dos ‘secciones’ están operando ‘en serie’ (una detrás de otra). Algunos sistemas de síntesis ofrecen también la posibilidad de generar comportamiento ‘elimina banda’ (con las dos secciones trabajando en paralelo y la frecuencia de corte ‘paso bajo’ por debajo de la frecuencia de corte ‘paso alto’).
Ofrecer esa variedad de comportamientos en tecnología analógica complica el diseño y obliga a disponer más controles en el panel, pero no es para nada desconocido. Sólo por mencionar algunos recientes, el Waldorf Rocket tiene un filtro analógico configurable entre paso bajo, paso banda y paso alto; o el Elektron Analog4 tiene dos filtros encadenados en serie, uno de ellos siempre paso bajo y el otro configurable entre varios modos (paso bajo, paso banda, elimina banda, paso alto, peaking,…).
En diseños digitales es más frecuente encontrar la posibilidad de variar el tipo de actuación del filtro, sin necesidad de ir a instrumentos ‘de alta gama’, pues es sólo cuestión de complicar el software y contar con un procesador de suficiente velocidad.
Otro día hablaremos más en detalle de filtros y escucharemos ejemplos de los distintos tipos, y de la diferencia entre el sonido de filtros de 12 y 24 dB/oct. De momento hoy, queremos seguir entendiendo algunos conceptos esenciales, y no tanto entrar en sus detalles y uso.
Filtros: la resonancia
[Índice]Una de las opciones que los filtros en los primeros sintetizadores analógicos podían ofrecer sin complicar mucho la vida a sus diseñadores era la de permitir el ajuste de la ‘resonancia’, también llamada factor ‘Q’ o ‘de calidad’ (y en los MS ‘peak’). Sin más que introducir un potenciómetro se podía ajustar este parámetro que afecta mucho al resultado sonoro y que por ello es muy usado y permanece como un parámetro esencial en cualquier filtro para sinte que se precie.
Incrementar la resonancia lo que hace es enfatizar las frecuencias más próximas a la frecuencia de corte en relación con las demás. Aquí tenéis nuevamente un ruido blanco pasando por un filtro, con el corte a 6 KHz y un alto grado de resonancia.
En el espectrograma se ve ahora que ese énfasis tan concentrado en una frecuencia concreta produce la aparición de una raya espectral sobre el fondo ruidoso. Y de hecho el resultado sonoro en este caso es el de un ruido en el que parece estar superpuesta una oscilación.
Aquí tenéis de nuevo la misma situación pero con el corte bajado a 1700 Hz, con lo que es más visible incluso en la forma de onda y en el espectrograma ese resultado que ‘recuerda’ a una oscilación senoidal pero inmersa en un mar de fondo ruidoso.
Obtenemos de esta forma ‘ruidos’ altamente coloreados, concentrados sobre una región del espectro. O incluso la sensación (si como en los ejemplos anteriores forzamos mucho la resonancia) de la presencia de un tono).
Pero muchas de las señales que tratamos son armónicas, tienen estructura armónica. La actuación de la resonancia en el caso de señales periódicas la veremos en un vídeo final que ilustra la actuación de la resonancia no sólo sobre ruido sino también sobre señales periódicas, armónicas, como las típicas de un oscilador. Esencialmente veréis que es posible enfatizar una región de armónicos o incluso un armónico concreto. En el vídeo crearemos un sonido que recuerda a la vocal 'A' precísamente imitando su formante o resonancia principal (sintonizando un filtro con resonancia en la zona de frecuencias en las que el tracto vocal produce más énfasis al producir el sonido 'A').
El factor Q o resonancia mide es la relación entre la ‘altura’ del pico y su ‘base’. Aquí tenéis una representación idealizada del efecto que causa sobre la respuesta de un filtro paso bajo un conjunto de diferentes factores Q.
Cuanto más subimos la resonancia el énfasis es mayor y a la vez más concentrado en una región más estrecha de frecuencias, es más estrecho y picudo. Lo que nos lleva a presentar otro concepto más.
Auto-oscilación en los filtros
[Índice]Cuando en un filtro se permite la modificación del factor de resonancia, el recorrido que admite ese factor ‘Q’ puede ser corto o extenso. Si el recorrido es corto podremos generar un pequeño énfasis en torno a la frecuencia de corte (las primeras curvas de la figura anterior). Si es extenso (si la resonancia se puede ‘subir’ mucho, como en la última curva, la de color más intenso) puede llegar a extremos que dan lugar a que el filtro comience a oscilar.
Es fácil de entender. La resonancia sube la ganancia del filtro en el entorno de una frecuencia concreta y cuanto mayor es esa resonancia, tanto mayor es la ganancia y tanto más concentrado sobre una frecuencia concreta su efecto (menos disperso).
Llega un momento en el que el filtro tiene tanta ganancia y tan concentrada que amplifica cualquier mínima cosa que exista (y el silencio total es inexistente, siempre hay algo). Y lo amplifica ‘sólo’ en esa frecuencia en la que está centrado el pico (tan estrecho es el pico de resonancia que es como si actuara en una ‘única’ frecuencia –o para mayor exactitud, en algo en lo que no podemos percibir la existencia de varias frecuencias: a efectos prácticos nos suena como un tono-).
Si el recorrido de la resonancia es tal que permite en su extremo alto provocar esos efectos, decimos que el filtro tiene capacidad ‘auto-oscilante’. Llega a oscilar, a producir una señal oscilante por sí mismo, sin depender de que exista un oscilador. Un filtro auto-oscilante permite generar señal incluso si no ponemos nada en su entrada.
¿Qué sucede si la señal de un oscilador atraviesa el filtro y este está ajustado de forma tal que auto-oscila?
Además de los picos debidos al oscilador, aparece un pico ‘extraño’ que no depende de la nota que hayamos ejecutado sino de dónde está ajustada la frecuencia de corte del filtro. Es decir, se superpone (se suma) la oscilación producto del filtro con la que viene del oscilador y que es filtrada.
Tal como apreciaréis en los ejemplos del vídeo de cierre podríamos ‘sintonizar’ la frecuencia de corte con alguno de los armónicos de la propia señal del oscilador (para enfatizarlo), o podríamos colocarlo ‘en medio’, entre las posiciones de los armónicos, para obtener esa inarmonicidad, que puede ir desde un batido, a una inarmonicidad evidente casi acampanada.
Es más, como en ningún sistema la ganancia es infinita, en realidad es imposible para un filtro auto-oscilante generar un tono puro. Lo normal es que la oscilación que generan esté ‘saturada’ (y por tanto mostrará algunos armónicos). Es tanta la ganancia del filtro en torno a la resonancia que las tensiones internas son muy grandes, tanto que a menudo exceden de lo que la alimentación (ya sea +/-12 voltios, +/-15 voltios, o la que sea) no puede llegar a ofrecer tensiones tan altas. En las partes del ciclo con valores extremos, el propio límite de la tensión máxima de la alimentación en el sinte llevan a que la señal se ‘achate’ en los extremos, se ‘sature’, está ‘limitada’… ya no es una senoidal pura, sino ‘recortada’. Y eso implica que tiene armónicos.
Es un efecto no lineal que aparta al filtro de su comportamiento normal (decíamos que un filtro se define como un sistema lineal e invariante). Pero es un efecto real que sucede por las limitaciones prácticas de los sistemas. La auto-oscilación generará una señal propia (al margen de lo que esté entrando al filtro) que se combina con la entrada y que además del esperado ‘tono’ a la frecuencia de corte contendrá algunos de sus armónicos. Nuevamente el vídeo lo ilustra.
Algunos estaréis pensando ya en cómo estas cuestiones afectan a la preferencia por unos u otros filtros, a la eterna discusión analógico electrónico vs. simulado, etc. Pero eso quedará para otro día. Antes de cerrar, la presentación del vídeo y un último aviso.
Un vídeo ilustrativo
[Índice]Se escucha tal cual la salida del iMS-20, pero habiendo anulado sus efectos y empleando una configuración que aplica un único VCO y un VCF paso bajo. De esa forma se asemeja al sonido ‘en bruto’ que produciría un MS-10. Aunque hay que insistir que no se trata de un vídeo ‘musical’, es todavía muy de presentación ‘de conceptos’ de filtros.
Espero que os guste aunque sólo sea por poder ‘ver’ lo que estamos acostumbrados a ‘oír’ (a través de espectrogramas y analizadores de espectros).
Ojo: ¿Filtros sin resonancia?
[Índice]Ya no es lo habitual, pero en su día muchos samplers y sintes, aunque contaban con filtros, carecían de la posibilidad de ajustar la resonancia. Algunos tan populares como el Korg M1 o los Alesis Quadrasynth sufrían de esta carencia. La falta de resonancia en los filtros, como podéis intuir, merma las capacidades como sintetizadores enormemente. Serán unos correctos ‘reproductores’ de las muestras que llevan internamente, pero no permitirán unas modificaciones del tipo que estamos acostumbrados a concebir como propias de un verdadero sintetizador.
Y por supuesto, olvidaros de la auto-oscilación en un filtro no resonante.

