Síntesis (9): Los filtros, ¿una gran mentira? (II)
- Distorsión en los filtros analógicos
- Distorsión en los filtros digitales: SIN modelado analógico
- Distorsión en los filtros digitales: modelado ‘barato’
- Distorsión en los filtros digitales: modelado ‘serio’
- Aliasing en los filtros digitales
- ¿Hay solución? Evitar el aliasing en los filtros
- Un ejemplo: el Solaris
- Otro ejemplo: Arturia Prophet V
- Comparación de filtros (MS-20 vs Prophet)
Completamos el estudio de ‘la gran mentira’ de los filtros para síntesis fijándonos en su comportamiento no lineal. Sobre todo nos da ocasión para pensar (seriamente) en el debate analógico/digital: ¿cuánto falta para que los bits cacen a los voltios?
Tal como veremos, los filtros usados en síntesis (al menos los más renombrados y deseados entre ellos), lejos de ser sistemas lineales (dedicados sólo a ‘retocar’ los niveles de las diferentes bandas de la señal, pero sin ‘inventarse’ nada) conllevan, con los ajustes habituales, unas dosis no desdeñables de distorsión.
Vamos a meternos en las tripas de un filtro analógico y luego en las de uno digital. Podremos así comparar cómo actúan uno y otro (en este caso centrándonos en los aspectos de este comportamiento no lineal). Y entenderemos porqué es cierto que en muchos casos no suenan igual, pero también entenderemos que las soluciones existen y que el que podamos disfrutar de filtros digitales con comportamiento analógico es perfectamente factible, aunque muchos fabricantes no nos lo quieran ofrecer (porque en realidad pocos usuarios son los que reclaman ‘de verdad’ -pagando un mayor precio- esas finuras).
Distorsión en los filtros analógicos
[Índice]Hablábamos en la entrega anterior de las grandes tensiones internas que se generan en los filtros cuando aplicamos resonancia. En un diseño analógico esas tensiones grandes no ‘caben’, no se pueden soportar porque la alimentación y las características de los componentes imponen un límite a la tensión máxima tolerable. Por tanto aparece (en los valores internos del filtro) una saturación (que siendo analógica es ‘suave’, con codo en curva).
Pero fijaos en lo que he dicho: lo que se satura son los valores internos que el filtro emplea al realizar sus ‘cálculos’ sobre la señal. El efecto que esa saturación de sus ‘variables internas’ puede llegar a tener sobre la señal, es bastante más complejo que la mera saturación de la señal.
Para poder profundizar luego, pensemos primero en un elemento que aporte saturación directamente sobre la señal, un elemento de distorsión ‘independiente’. Sería el caso de cualquier amplificador (ya sea un previo o un ampli de potencia). Como hay un límite siempre a la máxima tensión que el amplificador puede generar, tanto saturará a niveles altos: recortará los picos de la señal cuando esta sea grande (no así cuando sea pequeña):
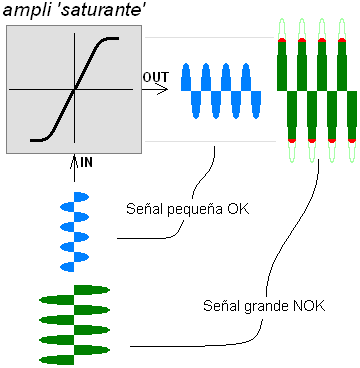
Pero volvamos a nuestros filtros. Si pensamos por un momento en el diseño de un filtro cualquiera, como por ejemplo el clásico filtro ladder (escalera) presente en los Moog y tantísimos otros sintes, la forma en la que consigue la caída de 24dB/octava es acumulando varias etapas simples de 6dB/octava. Cuatro concrétamente. Y cada una es un pequeño amplificador (de ganancia unidad) pero que por llevar un condensador en sus tripas elimina las componentes de alta frecuencia (y tiene por tanto globalmente un comportamiento paso bajo). No vamos a contar el funcionamiento de la electrónica en detalle, nos basta esa idea general. Y cada una de esas 4 etapas es en sí mismo un elemento que puede ‘saturarse’. No llegaría a saturarse (salvo que la entrada tuviera un valor grande) por tratarse de una etapa de ganancia unidad, pero la presencia de la realimentación cambia las cosas.
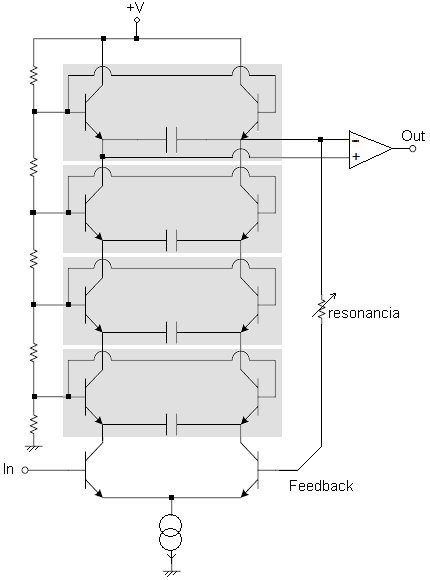
Al introducir la realimentación, la señal original y la realimentada se suman, y podemos tener ya una ‘gran’’ señal interna (aunque no lo sea externamente). En definitiva cuando aumentamos la resonancia, las tensiones que intervienen en esas etapas crecen. Pero no pueden crecer indefinidamente (por la limitación que impone la alimentación). Y las interacciones (debido a los distintos ‘lazos’ que existen en el circuito y a la acumulación de las 4 etapas) distan de ser simples. Pasaría algo parecido con otros diseños que no fueran este ladder. La distorsión que genera el filtro no es una distorsión ‘a posteriori’, tras el filtrado, sino que está ‘imbricada’ en el propio filtrado.
El resultado final es una posible distorsión que no sólo aparece cuando la señal de entrada es grande, sino también cuando la ‘realimentación’ (la resonancia) es alta. La presencia de condensadores hace que esa distorsión tenga además ‘memoria’, que no sólo afecte instantáneamente. La distorsión puede ‘manchar’ más allá de los picos de la señal de entrada, puede extenderse y durar un poco más.
En definitiva resultará un patrón de distorsión que (en función de cómo sea el diseño del filtro) puede llegar a ser bastante complejo (comparado con la mera saturación instantánea).
Cuando exageramos más la resonancia (haciendo que aparezca la autooscilación) el comportamiento no lineal es evidentísimo.
La figura muestra la aparición de rayas espectrales que son producto claro de la distorsión. Hemos marcado dos de ellas en baja frecuencia, que es fácil asociar a la distancia entre la frecuencia de resonancia (676 Hz.) y los dos armónicos de la señal del oscilador más próximos a ella (787 y 525 Hz.). pero se aprecia igualmente otra múltiple actividad y picos en el espectro.
El efecto más patente (y más fácil de observar) en relación con esa no linealidad en los filtros es el que sucede cuando forzamos su autooscilación. Cabría esperar que sólo se produjera oscilación sobre una única frecuencia (la de resonancia), pero en la práctica aparecen acompañándola varios armónicos (porque, de forma parecida al ejemplo del amplificador, los picos de la señal se deforman).
Esta es, de hecho, una buena forma de cotejar cómo es la respuesta no lineal de un filtro. La imagen del espectro de la autooscilación de un filtro os dice bastante de cómo es el tipo de distorsión que puede tender a generar.
Por ejemplo, aquí teneís el iMS-20 para iPad puesto a autooscilar (y habiendo anulado los osciladores). Es llamativo que la autooscilación en este caso sólo genera armónicos impares lo que indica la presencia de una distorsión simétrica (luego volveremos sobre ello).
Aquí tenéis un vídeo ilustrando (para que también pueda oírse) estas cuestiones que estamos comentando.
Distorsión en los filtros digitales: SIN modelado analógico
[Índice]Pensad ahora en un filtro digital.La forma en la que funciona es que recibe las muestras de la señal, conserva (y actualiza) internamente las más recientes, y las combina para generar la señal de salida, y además tiene un camino ‘de realimentación’ por el que también las muestras recientes de la salida intervienen en los cálculos. No me pidáis aquí que sea muy detallista. Igual que no he contado, sólo pintado, las tripas del filtro ladder analógico, no pretendo aquí contar las de un FIR o un IIR digital (al menos no hoy).
Lo que me importa es que está combinando un pequeño repertorio de los últimos valores (muestras) de la entrada y la salida (y los está sumando tras multiplicar cada una de ellos por un coeficiente –los valores de esos coeficientes c0, c1,… y c1’, c2’, … son los que determinarán la respuesta del filtro-). La salida se obtiene como una suma de productos (aquí no hay condensadores, ni transistores…).
Como podéis ver este diseño ‘directamente’ digital (no un modelo fino de un circuito analógico) no tiene ningún parecido en la estructura con la que realiza el filtrado. Puede imitar el comportamiento del filtro, pero no su estructura interna. Y la distorsión que aparecía en el caso analógico tenía que ver con la tecnología y la estructura de esa realización analógica.
Hay una diferencia importante respecto a la realización analógica. Esos valores internos ‘grandes’ (que en un sistema analógico se saturan de forma progresiva, con un codo suave), en un sistema digital fácilmente se ‘recortan’ (codo duro) cuando se llega al valor límite. Y eso es algo que se nota. Siempre. La saturación suave analógica frente al recorte digital.
En los primeros tiempos (diseños de filtros con 12, 16 o 24 bit en los cálculos, pero en todo caso con coma fija) la saturación de los valores era brusca y muy presente: al llegar al valor máximo digital con esa profundidad de bits. Y ese codo duro es siempre menos ‘dulce’ en su acción distorsionadora que el correspondiente codo blando al que estábamos acostumbrados de la época analógica.
Este tipo de diseño puede aún encontrarse en algunos sistemas digitales, aunque hace ya años va desapareciendo el uso de coma fija en los cálculos y se emplea de forma más generalizada el cálculo en coma flotante (básicamente porque ahora los procesadores de coma flotante son habituales y nomucho más caros). De hecho veréis algunos plug-ins que presumen y detallan entre sus características esta. La del formato interno de los cálculos. Ya veis que no es una cuestión baladí.
Demos por hecho (porque es lo que está sucediendo) que salvo en productos muy ‘gama baja’ ya se estén aplicando cálculos en como flotante. Magnífico: no hay problema, los valores internos pueden crecer y ‘caben’ en esa representación de coma flotante. Ese parecería el razonamiento.
Pero sigamos pensando lo que eso significa. Con la representación de coma flotante y con una amplia profundidad de bits, los valores en la práctica no conocen límites (desde luego mucho menores que la limitación por alimentación en un analógico). Y esto puede llevar a la desaparición de la saturación, y con ello a la pérdida de parte de ese carácter que nos gustaba encontrar en los filtros a los que estábamos acostumbrados. Podremos tener una resonancia más limpia que en analógico, pero por eso mismo una resonancia que pierde algo de su fiereza. Con facilidad esos filtros digitales son demasiado lineales para nuestro gusto, y eso les resta carácter.
Estas versiones de filtros digitales no son una buena recreación del filtro analógico. Pueden ser unos buenos filtros, quizá incluso ‘mejores’ (técnicamente, más lineales), pero pueden defraudarnos en sus resultados porque echemos en falta la ‘magia’ analógica.
Distorsión en los filtros digitales: modelado ‘barato’
[Índice]Una realización digital que quiera recuperar la esencia analógica debe preocuparse por reintroducir (es perfectamente factible) la distorsión y el comportamiento no lineal.
Este tipo de detalles diferencian un filtro digital ‘convencional’ (o ‘nativo digital’ para que me entendáis mejor) de un filtro digital para modelado analógico, un filtro que quiere ‘imitar’ el comportamiento analógico desde una implementación digital, en lugar de beneficiarse de la posible mayor ‘fidelidad’ digital.
Una forma sencilla, con un coste computacional muy bajo (algo que a los fabricantes les interesa) sería introducir una no linealidad (alguna saturación instantánea) en algún punto del filtro (ya sea en su salida, o, mejor, en algún punto ‘interno’). Eso permitiría aportar el añadido de distorsión.
Por situaros en alguna fecha, en los 90 desde el ámbito de la investigación y las universidades se proponían se proponían este tipo de actuaciones. Y varios productos pretendidamente de ‘modelado analógico’ se limitan a algo como eso.
No es lo ideal. Si se mantiene la estructura ‘nativa’ de un filtro digital y sólo se le añade distorsión, aunque sea ‘a mitad de camino’, lo que obtenemos es un nuevo modelo de filtro con no linealidad, pero no es realmente una recreación de ningún modelo ‘clásico’.
Tendrá una personalidad, un carácter, sin duda. Pero no será la misma que la que manifiestan los diseños clásicos analógicos.
No los llamaría yo por tanto filtros ‘virtualmente analógicos’ o ‘de modelado analógico’, sino sencillamente filtros digitales con distorsión interna. Podrán sonar magníficamente (o no, en función del acierto del diseñador al ubicar la saturación y definirla), pero no serán una ‘recreación’ del pasado sino una nueva variante.
Decía que una actuación de ese tipo (que es la que está detrás de muchísimos sistemas supuestamente ‘analógicos virtuales’) es muy cómoda para el fabricante porque no exige demasiado cómputo. ¿Porqué quiere el fabricante que no se dispare el cómputo? Porque, siendo realistas,¿en qué se fija la mayoría cuando compra un nuevo sinte digital: en que tenga polifonía de 100 voces o en que recree con gran precisión un filtro ‘antiguo’? El fabricante necesita la capacidad de cómputo del procesador que use en el diseño digital para ofrecernos más voces, más efectos simultáneos, más de aquí y de allá, pero muy pocos van a comprar fijándose en la fidelidad del modelo del filtro.
Por alguna extraña razón, nos quedamos muy felices pagando muchísimos euros por un sinte analógico viejo (perdón, clásico) de exigua polifonía (quizá incluso monofónico), sin efectos (como mucho un chorus ruidoso), etc… (no levantéis las armas: lo digo con el cariño de quien casi vió nacer a esas queridas máquinas). Pero con la misma exageración nos resistimos a pagar esa cantidad por un sinte digital con verdadero y detallado modelado analógico, y nos quejamos de que ese modelo tiene poca polifonía, o de que sus efectos son más pobres que los de cualquier ‘workstation’ barata, etc.
Distorsión en los filtros digitales: modelado ‘serio’
[Índice]La opción del modelado ‘barato’ anterior es cómoda para el fabricante y no tiene porqué interpretarse como un ‘mal’ filtro. Es sencillamente un filtro distinto.
Pero si queremos ir más al detalle, hasta el punto de obtener una verdadera recreación en digital de un filtro analógico, hay que aplicar modelos más finos.
El análisis de los filtros suele hacerse con herramientas de análisis lineal (respuesta impulsiva, respuesta en frecuencia, etc.) que son incapaces de responder al 100% como lo haría el sistema real que queremos emular (porque en el sistema real, tal como hemos dicho, hay componentes de comportamiento no lineal).. Lo que hay que hacer (y es algo razonablemente factible) es imitar el circuito (por ejemplo el ladder). No sólo pensar en que hay un ‘in’ y un ‘out’ sino modelar la actuación de cada etapa, e incluso de cada transistor, de cada condensador, etc. Hacer un modelo digital del circuito. Pero eso significa que el cálculo se dispara.
Los que queráis profundizar en los aspectos de diseño internos a los filtros digitales, podéis por ejemplo leer este artículo (‘Non-linear implementation of the Mogg ladder filter’) http://dafx04.na.infn.it/WebProc/Proc/P_061.pdf que es del año 2004 (lo digo para que sigáis teniendo una referencia temporal de cuándo se están estudiando estas cosas a este nivel de detalle: no hace tanto).
De forma muy resumida, en ese artículo se usa un modelo ‘fino’ de cada etapa del ladder. Aunque el modelo en coma flotante permita que las variables crezcan casi ‘sin fin’, el modelo fino limita cada una de las etapas de forma equiparable al caso analógico. No es una distorsión única e instantánea situada al final del filtro, sino un modelo que emula el comportamiento detallado de cada etapa y las combina con mucho mayor paralelismo al sistema analógico original.
Pero cuando lo hacemos, aparece otro de los ‘diablos’ de los sistemas digitales: el aliasing. Para comprender el porqué no hace falta conocer toda la ingeniería que exige ese artículo, podemos entenderlo también desde un ejemplo y una explicación más simple, que hacemos en el siguiente apartado.
Aliasing en los filtros digitales
[Índice]Os muestra la figura siguiente el resultado obtenido con un iMS-20 haciendo que el filtro autooscile (y habiendo anulando la señal de los osciladores). Como podéis comprobar, el modelo es tal que está generando distorsión: en lugar de una única raya espectral a la frecuencia de corte aparece toda una serie de rayas (las he recalcado un poco más gruesas para que las veáis mejor, pero es el único retoque que hay en la figura).
Obviad la pésima calidad de la grabación (el nivel de ruido que la acompaña es avergonzante: está capturado con la entrada de audio de un PC de sobremesa, sin mayores cuidados). Lo que me interesa que veáis es que la oscilación que se produce tiene una larga lista de armónicos, con amplitudes nada desdeñables. Esas componentes son producto de la distorsión dentro del filtro. Supongo que os ha llamado la atención la presencia exclusiva de los armónicos impares, lo que nos indica que este ‘filtro+distorsión’ está operando de una forma simétrica. Algo que difícilmente sucedería en un analógico verdadero, pero que aquí se manifiesta de forma muy rotunda. No sé si el MS-20 original tenía esta característica de ‘distorsión impar’, aunque no lo creo. Es muy posible que el filtro haya sido emulado ‘razonablemente’ en cuanto a su respuesta en frecuencia como filtro, pero quizá no tanto al forzar estos extremos del comportamiento que lo llevan a una zona no lineal.
Pero lo más rotundamente llamativo es que (tal como os he marcado con verde y rojo en la figura) la serie se extiende tanto que en la realización digital (hecha sin el suficiente ‘mimo’ para estas cuestiones) se está produciendo ‘aliasing’: las frecuencias superiores a la mitad de la frecuencia de muestreo no admiten una representación fiel en la versión discreta y ‘se vuelven’ hacia frecuencias inadecuadas (y que rompen la armonicidad que cabía esperar en la serie –en la figura los armónicos 21f, 23f, 25f y demás ya no son tales, aparecen reflejados y en frecuencias que sin i.propias de la serie-).
En definitiva los armónicos producidos en la distorsión (que en el caso analógico podían subir en frecuencia sin límites duros), en una realización digital pueden llevar con mucha facilidad a provocar aliasing. Se vé muy claramente en el ejemplo anterior. Pero de la misma forma, cualquier no linealidad (y cuando el filtro usa gran resonancia pero por debajo de la autooscilación casi siempre habrá distorsión), puede estar enfrentando problemas de aliasing (incluso tratando una única voz, monofónica, con un solo oscilador periódico). El aliasing hará que las componentes nuevas creadas no sean armónicas con el contenido de la señal original. Inarmonicidad, aliasing… horribles artefactos digitales.
¿Hay solución? Evitar el aliasing en los filtros
[Índice]En procesado digital que conlleve distorsión, una de las conclusiones importantes es la necesidad de realizar los cálculos con un alto factor de sobremuestreo. Acudir a diseños en los que el filtro opere con un alto factor de sobremuestreo (aunque su entrada y su salida se ofrezcan, por ejemplo, a 48KHz de frecuencia de muestreo, quizá los cálculos internos se realicen a 192KHz o más). Eso eleva el límite de Niquist durante los cálculos.
¿Habéis visto ya algunos productos que describen que los cálculos se realizan con sobremuestreo x2, x4 (o por lo que sea)? Ahora sabéis porqué es importante. Es un detalle que pocas veces atendemos, pero que como veis tiene importancia (me permito recomendaros otro artículo que escribí, a propósito de la cuestión del que yo denomino ‘muestreo crítico’).
Un ejemplo: el Solaris
[Índice]Sin ir más lejos el ‘Solaris’ (ese sinte que muchos reverencian pese a que pocos le han puesto la mano encima –y posiblemente pocos se la pondrán-) indica entre sus características el que los cálculos internos se realizan a 96KHz. Por algo será.
No puedo hablar de él (no lo he probado, aunque no me importaría nada ;->), pero lo uso como ejemplo de que sólo con esas opciones (un cálculo mucho más intesivo que a 48KHz, y que exige mejores procesadores) es posible ofrecer lo mejor de los dos mundos: la fiabilidad y flexibilidad digitales, con el querido color analógico. Pensad que en el Solaris hay nada menos que 6 procesadores SHARC operando simultáneamente. Y pese a ello, se publicita como una gran ventaja frente a otros que “incluso con un sonido complejo que use cuatro osciladores, cuatro filtros, cuatro mezcladores y saludables dosis de modulación, ¡puedes conseguir una polifonía de 10 voces!”.
En condiciones parecidas (4 osciladores, 4 filtros, muchas rutas de modulación, etc.) un módulo General MIDI puede ofrecer fácilmente 32 voces (por ejemplo todos los descendentes de los Fantom de Roland) y cuesta diez veces menos. Pero, no, esos módulos no son ‘modelado analógico’ y no trabajan con sobremuestreo.
Podéis entender ahora algo mejor porqué hay que pagar tanto por una máquina como esta (o cualquier otro verdadero modelado analógico fino). No es sólo (aunque también) el que el coste de disponer de multiplicidad de controles en el panel frontal es alto. Es mucho más importante cara al coste lo que no se ve. El diseño interno del código que ha de emular las reacciones propias del mundo analógico no es fácil, y también exige una importante cantidad de ‘maquina’ para soportar el coste computacional de una emulación correcta.
En línea con lo que estamos contando en este artículo, entenderéis ahora perfectamente porqué se preocupan tanto de insistir en la publicidad del Solaris en que ‘internamente, todas las operaciones son en coma flotante 32bit y las señales de audio y los buses funcionan a 96 kHz para una excelente calidad de audio’. No podéis esperar que suene ‘analógico’ sin esos atributos.
No es precisamente lo que encontraremos en productos de gama baja (ni media, ni en buena parte de la alta). Estamos hablando de lo que todavía son ‘diamantes’ dentro de la oferta de sintetizadores digitales. Pero ciertamente, el atractivo de los filtros analógicos puede obtenerse también en realizaciones digitales. Esos sistemas digitales con recreación cuidadosa de las cualidades (en realidad defectos agradables) de lo analógico pueden ser hoy día caros, ‘de muy alta gama’, pero bien sabemos que el soft (al contrario que el hard) acaba por reducir su precio a medida que se estandariza. Al menos es el futuro es nuestro.
Otro ejemplo: Arturia Prophet V
[Índice]En la web de Arturia (bien conocidos por su amplio catálogo de recreaciones de modelos clásicos en software) a propósito de los filtros en el Prophet V, aparece esta gráfica comparando el resultado de la autooscilación del filtro en el Prophet 5 original, y el de su recreación ‘íntima’ del filtro por parte de Arturia en su versión software (he retocado la gráfica para facilitar su lectura). Las dos líneas muestran una gran semejanza. Y creedme que la recreación fiel del patrón de armónicos producto de la autooscilación es una de las ‘pruebas de fuego’ para valorar la calidad de la recreación de la ‘esencia’ de un filtro (mucho más que el que respete su pendiente u otras cuestiones relacionadas con su respuesta en frecuencia cuando actúa con una acción de filtrado más lineal). Parece por tanto que Arturia (si damos crédito a esta figura de su web) ha hecho un buen trabajo recreando el Prophet.
Por cierto, y ya que estamos con esa gráfica: ¿habéis visto que la serie se corta? ¿Porqué no aparece la siguiente raya? Lejos de intentar extenderse hasta los 20 KHz, el diseño ha preferido ‘cortar’ bastante antes. Fijaos que la gráfica sólo muestra los primeros 10KHz y que las rayas se cortan antes incluso de esa frecuencia. Realmente, a -80 dB respecto al pico principal la contribución de esas rayas superiores que aquí parecen faltar es ciertamente menor. Hubiera sido interesante ver realmente el espectro del Prophet V (en el que sospecho sí habría aparición de algunas otras rayas). Es muy complicado (difícil de creer) que un circuito analógico genere esas 5 rayas sin generar la sexta (salvo que se deba a que el Prophet tenga su salida de audio limitada a un ancho de banda de unos escasos 9KHz).
Pero si nos centramos en valorar el esfuerzo de Arturia (dando crédito a estas gráficas) habría que aplaudirlo. Está claro es que si no se corta la serie de forma temprana existe el peligro de que aparezcan componentes altas que puedan provocar aliasing (lo que sí hubiera sido muy apreciable a pesar de esos bajos niveles). Es mejor diseño imitar los primeros y más prominentes productos de la distorsión que pretender extenderlos y con ello introducir aliasing.
Hubiera sido también interesante ver gráficas de ese tipo para otras frecuencias de resonancia, y para otros de los sintes modelados por Arturia (si estudiáis el Prophet V original tampoco ‘brillaba’ tantísimo, mientras otros sintes sí –y con ello el peligro de aliasing sería mayor con esos otros sintes y obligaría quizá a ir a sobremuestreo en los cálculos, tal como realiza Solaris-).
Comparación de filtros (MS-20 vs Prophet)
[Índice]Podemos aprovechar las dos últimas gráficas para mostrar también cómo podemos ‘entender’ la magia y personalidad de unos y otros filtros en sintes. No creo que nadie que los conozca dude de que el MS-20 es un sinte con filtros ‘duros y generosamente chirriantes’, mientras que el Prophet V tiene comparativamente unos filtros más ‘suaves y cálidos’. Podemos en las gráficas ver el porqué.
Si comparáis el patrón del iMS-20 y el del Prophet, claramente el filtro del iMS-20 es más 'sucio' y distorsionante (con la molestia añadida de un patrón de distorsión marcadamente impar), mientras que el del Prophet es comparativamente suave (armónicos pares e impares, rápidamente decrecientes en nivel, y con niveles claramente más reducidos).
No son desde luego los filtros los únicos elementos que determinan el sonido final de un sinte. Pero como siempre insisto, en mi opinión (y la de muchos) al sintetizar mucho más que los timbres estáticos nos interesa cómo llega a ser la ‘dinámica tímbrica’. Nuestro elemento principal para la modificación del timbre en síntesis sustractiva son los filtros, y por tanto en ellos tenemos siempre un interés muy especial.
La próxima vez que un filtro os guste, ya sabéis: lo ponéis a autooscilar en unas cuantas frecuencias, grabáis el resultado, obtenéis su representación espectral y pensáis en dónde radica su magia. Puede ser el primer paso para acercarse a ella desde otro sintetizador diferente.
