Posición de Fase y Amplitud Relativa
01/11/2008 por
Arnold Salgado | 2 min de lectura
Hola a todos, hoy presento un archivo al que le he nombrado "graficador" de fase, para facilitar la compresión de la fase de ondas sinusoidales, como también apreciar que su amplitud es dependiente de la fase y observar que la misma está desde los primeros pasos del maravilloso mundo de la física.
Para esto, un claro ejemplo de lo que es la posición de fase con respecto al eje de un objeto, es lo que se analiza en movimiento circular de cinemática, veamos:
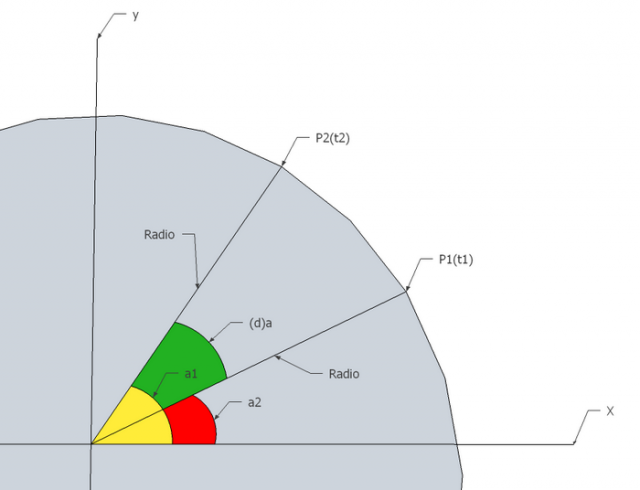
Donde: a=ángulo, (d)=diferencia.
De esto concluimos que, para que exista tal desplazamiento angular (a1, a2) o de fase, tiene que haber un tiempo que permita el transcurso de rotación de este objeto (P1, P2), por otro lado, el tiempo para completar su ciclo equivaldrá a una distancia total que más tarde es considerada como longitud de onda y periodo, pero también tendremos presente que eso implica desplazarse 2π radianes o 360° a lo que yo le llamo “distancia equivalente”.
Ahora, a la rama que le corresponde mostrar sobre fase y de forma detallada, es el movimiento ondulatorio. Esta viene dada por la siguiente ecuación:
Y(x,t) = Ym * sen (kx - wt)
Y(x,t) = Ym * sen (kx - wt)
Donde tenemos presente que no existe desplazamiento alguno en el tiempo, para que esto ocurra ha de introducirse en la ecuación la constante de fase.
Y(x,t) = Ym * sen (kx - wt - Φ)
Y(x,t) = Ym * sen (kx - wt - Φ)
Es esta ecuación la que determina la posición de una partícula en función del tiempo y su posición en el espacio como su amplitud, veamos la forma de la onda.
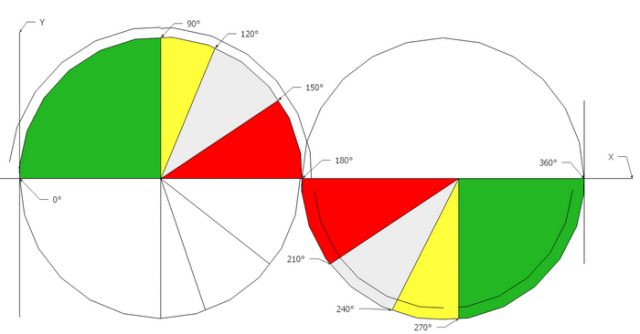 Como es de saber la amplitud de la perturbación de una onda sonora en un momento dado, es dependiente de la posición de la partícula en función del tiempo, por lo que este valor puede ser calculado mediante una función trigonométrica con origen en un plano cartesiano y aunque al parecer le estamos dando vueltas al asunto, solo se intenta ver el mismo caso desde otras perspectivas.
Como es de saber la amplitud de la perturbación de una onda sonora en un momento dado, es dependiente de la posición de la partícula en función del tiempo, por lo que este valor puede ser calculado mediante una función trigonométrica con origen en un plano cartesiano y aunque al parecer le estamos dando vueltas al asunto, solo se intenta ver el mismo caso desde otras perspectivas.
Para simplificar todo, vayamos a un caso más práctico:
Ejemplo:
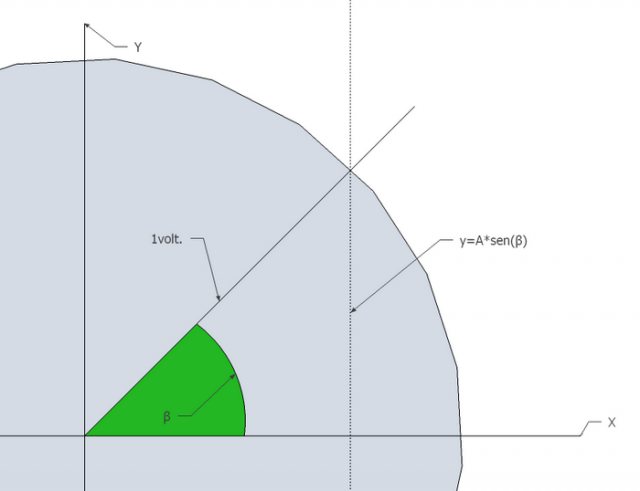
Tomemos un vector cuyo radio (Mov. Cir.) o modulo (Plano Cart.) es equivalente a 1volt a una frecuencia de 1kHz. Cuando han pasado 0,125ms por regla simple de trigonometría el valor que este vector va a tener siendo su equivalente a 45°, se calcula de la siguiente manera:
Tomemos un vector cuyo radio (Mov. Cir.) o modulo (Plano Cart.) es equivalente a 1volt a una frecuencia de 1kHz. Cuando han pasado 0,125ms por regla simple de trigonometría el valor que este vector va a tener siendo su equivalente a 45°, se calcula de la siguiente manera:
Y = A * sen (β)
Y = 1 * sen (45º)
Y = 0.707v
Y = 1v @ 90º
Y = 0.707 @ 135º
Y = -0.707 @ 225º
De esta forma se puede calcular la amplitud instantánea en cualquier punto del espacio, donde la onda se está desenvolviendo.
Lo que muestra el graficador:
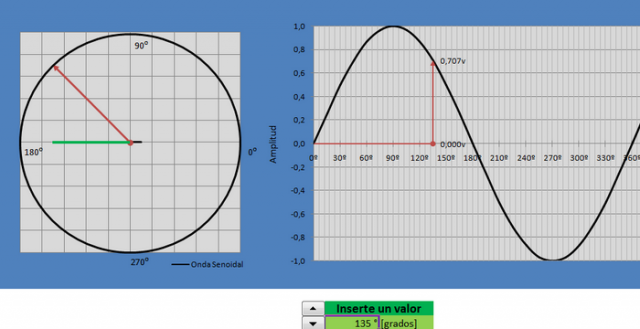
Esto ayuda a entender como el ciclo de la partícula vuelve a su posición de inicio y aunque existe desplazamiento angular como función del tiempo la partícula no cambiado de lugar.
Esto es la base para, más tarde, comprender de manera fácil el factor de cresta de una onda sinusoidal.
El archivo compilado en Excel esta disponible para descargar el siguiente enlace:
https://docs.google.com/open?id=0B1r5DSgmQqXhWHo4VXgtc1ZsRUk
¿Te gustó este artículo?



