Sinusoides y sonidos compuestos: armónicos y parciales en audio
- El ideal sinusoidal y su porqué
- Periodo, frecuencia y longitud de onda
- El tono puro o sinusoide
- Un ejemplo de señal compleja
- Armónicos y parciales, concepto del ‘fundamental’
- Diferencias de nivel entre parciales = diferentes formas de onda
- Fundamental como fundamento, no como principal
- Una clasificación de los tipos de sonidos
- Más lecturas y ejemplos audibles
Señales cíclicas, frecuencia, periodo, longitud de onda, parciales, armónicos, fundamental… Proseguimos nuestro curso de acústica y electrónica en audio interesándonos por aclarar estos conceptos esenciales y evitar algunos errores de interpretación. Lo hacemos a partir de una mirada y reflexión en torno a las sinusoides y su papel como elemento básico para construir otras señales más complejas.
Y es que muy a menudo al representar señales, y en particular señales sonoras, acudimos a pintar señales de tipo seno como primer ejemplo (también nosotros en la anterior entrega). Es la del seno una forma de señal peculiarmente importante, con características muy singulares, presente en multitud de fenómenos físicos y que actúa como pilar con el que se forman otras señales más complejas.
[Nota: Que no os extrañe si algún ejemplo y/o alguna gráfica ya os suena. Como parte de esta entrega repetiré algunas cuestiones ya presentadas en nuestro curso sobre síntesis]
El ideal sinusoidal y su porqué
[Índice]El seno, suavidad sin fin
[Índice]Sin entrar en matemáticas, todos entendemos que una forma curva de una particular perfección es la circunferencia, su curvatura es siempre idéntica, pero eso hace que se cierre sobre sí misma. Nuestras señales audio se desarrollan en la línea del tiempo, sin vueltas atrás. Si imaginamos un círculo rodando y nos fijamos en cómo evoluciona una marca que hayamos pintado en su perímetro, el recorrido que traza ese punto desarrolla una forma que llamamos sinusoidal, y que es la representación de la función seno. Ese recorrido sinusoidal tiene propiedades de extrema suavidad heredadas de su origen circular.
La estructura repetitiva y sin saltos de la onda en forma de seno está acompañada de una característica especial: su derivada de cualquier orden nos vuelve a llevar a una forma sinusoidal. Eso implica que un movimiento que siga un patrón tipo seno, tiene también una variación de su velocidad que es sinusoidal (por tanto también ‘suave’ y sin saltos), pero además su aceleración es igualmente de tipo sinusoidal, y así podríamos seguir. No deja de ser una característica curiosa en lo matemático, pero que además hace tremendamente suave el resultado de cualquier variación o movimiento: no encontraremos en los senos ninguna discontinuidad o salto. Ni en su recorrido, ni en su pendiente, ni en la pendiente de su pendiente, … es pura suavidad de orden infinito.
De hecho, usada como señal para modular parámetros audio, una sinusoidal genera un resultado tan fluido que no detectamos ninguna singularidad en su recorrido, mientras una variación triangular, pese a ser continua y sin saltos, tiene una discontinuidad en su pendiente (el cambio abrupto que se produce en sus vértices) que sí llega a poderse apreciar en muchos casos a oído. De ahí el uso preferente de la forma seno en tantísimos efectos audio (como en los retardos modulados, por ejemplo). Con otras formas de variación resultarían más duros en su actuación.
Pieza en la construcción de otras señales
[Índice]Más allá de esa singular suavidad, es relevante que los senos aparecen en una amplia cantidad de procesos físicos, aunque su extrema pureza hace que no se presenten en la práctica salvo de forma aproximada. El modelo de movimiento pendular es de tipo sinusoidal, por ejemplo.
Pero para nosotros un interés especial por los senos nace sobre todo del hecho de que otras señales de tipo cíclico (repetitivas, como lo son tantísimos momentos de los sonidos) pueden llegar a ser descritas como combinación de varias sinusoidales, es decir, admiten una descomposición como una familia de sinusoides. De hecho nuestro oído aplica a través de la cóclea un análisis de los estímulos auditivos que realiza esta descomposición en señales más simples de tipo seno.
La posibilidad de esa descomposición es algo ya demostrado desde las matemáticas por el Teorema de Fourier, y que varios experimentos físicos hacen evidente en la práctica. Así, es posible aflorar en experiencias fáciles de replicar que en muchos objetos vibrantes, caso especialmente claro en los instrumentos musicales, lo que sucede es en realidad la superposición de varios modos de vibración simultáneos, cada uno de ellos en sí mismo sinusoidal. Nos interesaremos por esta cuestión tras repasar los conceptos de periodo, frecuencia y longitud de onda.
Periodo, frecuencia y longitud de onda
[Índice]En cualquier señal cíclica, se pueden definir los parámetros, relacionados entre sí, llamados periodo, frecuencia y longitud de onda. Podremos encontrar muchas formas de ciclo, pero en la definición de periodo, frecuencia y longitud de onda es irrelevante esa forma, sea sinusoidal o más compleja.
El periodo (T) mide lo que dura cada ciclo de esa señal repetitiva. Es una medida de tiempo y por tanto en unidades de segundo (o alguna fracción como milisegundos). Esta figura representa dos señales con diferencias importantes en la forma de onda (una sinusoide, la otra más compleja) pero que tienen un mismo periodo.
La frecuencia (f) es el número de ciclos por segundo y se indica con unidad hercio (Hz) en honor a Herzt (aunque también a veces se encuentra indicada como ‘cps’ por ciclos por segundo, totalmente equivalente a Hz). Es evidente por sus definiciones que existe una relación inversa entre frecuencia y periodo.
f(Hz) = 1 / T(s)
T(s) = 1 / f(Hz)
La longitud de onda (λ) se refiere al espacio físico en el que se desarrolla cada ciclo dentro del medio en el que se esté propagando. Se trata pues de una distancia, y por tanto se mide en metros o sus fracciones. Lógicamente esa extensión depende de si el medio de propagación es uno u otro, por haber diferencias de velocidad de propagación.
Si llamamos v a la velocidad del sonido en m/s tendríamos esta relación para calcular la longitud de onda, llamada λ, a partir del periodo o de la frecuencia de la señal:
λ(m) = v(m/s) * T(s) = v(m/s) / f(Hz)
El interés de esas expresiones radica en que es difícil medir λ directamente. Al fin y al cabo no vemos el aire ni su compresión/rarefacción. Las relaciones anteriores permiten conocer su valor a partir de la frecuencia o del periodo, que sí son fáciles de medir. También serían factibles, aunque de escaso interés práctico, otras relaciones como f(Hz) = v(m/s) / λ(m) o como T (s) = c(m) / v(m/s).
Pensando en los extremos convencionalmente descritos para la audición humana, se dan estas correspondencias
| f | T | λ (para v=340m/s) |
| 20Hz | 50ms | 17m |
| 20kHz | 50us | 1,7cm |
De la importancia de estos extremos ya hemos hablado en la entrega anterior, en donde destacábamos la inhabilidad del oído para separar objetos sonoros semejantes que estén separados por menos de 50 ms., que acaban confundidos en uno de sonoridad alterada.
El tono puro o sinusoide
[Índice]El hecho demostrable de que otras formas de señal puedan describirse acudiendo a una combinación de sinusoides hace que las consideremos como la forma más simple posible en una onda, en tanto que las demás pueden ‘reconstruirse’ por agregación de múltiples sinusoidales. Por ello se llaman también tonos puros.
Buscando algo cotidiano que nos ofrezca una cuasi-sinusoide, podemos pensar en el sonido que emana de un diapasón poco después de que lo hayamos golpeado (el primer momento es demasiado ‘singular’ por culpa del impacto).
En el caso de una señal que, como el diapasón, desarrolla a lo largo del tiempo una forma sinusoidal, podemos hacer uso de la función seno para describirla como:
s(t) = A sen (2π f t + φ)
donde además de t como variable tiempo (s), aparecen
- f = frecuencia (Hz) de la senoide,
- A = amplitud de la senoide (en la unidad que sea apropiada), y
- φ = fase inicial (en radianes) -un parámetro que estudiaremos más adelante-
Un ejemplo de señal compleja
[Índice]Planteémonos el sonido de una cuerda ya sea pulsada/percutida o frotada con arco. El sonido que emana de ella es claramente mucho más complejo y rico que el del diapasón.
En el caso del frotamiento, la presión del arco sobre la cuerda la desplaza gradualmente de su posición de reposo y eso incrementa la tensión. Hasta que llega un punto en que la tensión es tal que la cuerda puede 'escapar' súbitamente del agarre al arco. Se produce un desplazamiento brusco al que seguirá una repetición de este patrón con de nuevo un desplazamiento gradual. Si os imagináis mentalmente la película, es desplazamiento de la cuerda acaba teniendo un patrón, una forma de ciclo, que asemeja ser una sucesión de rampas, al modo de lo que viene a ser el perfil de los dientes de una sierra. Eso es lo que nos dice una cierta intuición sobre cómo funciona. Su movimiento, y por tanto su sonido debería ser una sucesión de ciclos semejante a esta:
Nos interesamos ahora por su descomposición en vibraciones más simples. Es un hecho físico que en esa vibración compleja de la cuerda se superponen muchos modos diferentes, cada uno de ellos asimilable a una sinusoidal, y con esa peculiar relación entre sus frecuencias (todas múltiplos de una determinada). Imaginemos una cuerda cuya longitud hace que produzca la nota ‘La’ central. Desde luego dicha cuerda vibrará a 440 Hz., pero, aunque nos cueste verlo, también vibra simultáneamente a 880Hz., 1320 Hz., etc. (los sucesivos múltiplos de 440). Puede parecer extraño, porque no tenemos sensación auditiva de oír esos varios tonos puros, sino de oír una única nota, un único objeto sonoro, sin ‘partes’.
No con ánimo de demostrar nada, sino sólo de ilustrar, pensemos en una cuerda percutida. Oscila en toda su longitud con una frecuencia que depende de esa longitud y de la rigidez/tensión de la cuerda, pero además cuando la percutimos también oscila en un segundo modo el doble de rápido en el que ambas mitades se mueven en sentidos contrarios: una mitad de la cuerda sube mientras la otra mitad baja. También vibra en un tercer modo, en el que la cuerda parecería subdividida en tres fragmentos con el centro moviéndose en oposición a los extremos. Y así podríamos seguir con la cuerda concebida en cuatro fragmentos, en cinco, etc. Cada uno de estos modos de vibración de tipo sinusoidal y es de menor nivel (menor intensidad) que el anterior. El movimiento final de la cuerda es el resultado combinado, como también lo es el sonido que emana de ella .
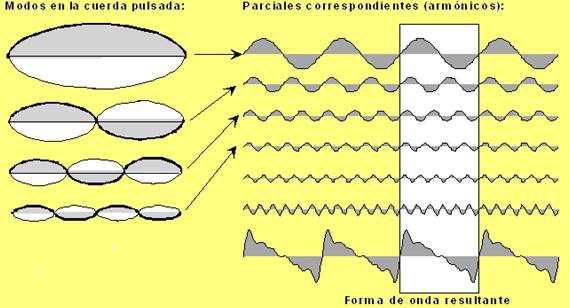
El de la cuerda (igual sucedería con cualquier otro elemento musical u objeto acústico) es por tanto un sonido ‘complejo’ (compuesto) en el sentido de que está formado por varias vibraciones sinusoidales superpuestas. La forma de onda resultante, el sonido que podemos escuchar o grabar, es la suma de esas diversas componentes.
Esa combinación de senoides, con frecuencias que son múltiplos sucesivos y que tienen cada una diferentes amplitudes (A0, A1, A2, A3,…) correspondería a
s(t) = A0 sen (2π*f*t+φ) + A1 sen (2π*2f*t+φ) + A2 sen (2π*3f*t+φ) + A3 sen (2π*4f*t+φ) + …
En el caso de que A1=A0/2; A2=A0/3; A3=A0/4, … (es decir, una caída progresiva hacia niveles cada vez más bajos con esa regla de amplitudes) la forma de onda obtenida resultante tiende hacia una rampa, y la sucesión de varios ciclos parece formar el contorno de la hoja de un serrucho. De hecho se habla de forma de onda en ‘diente de sierra’ (tanto más perfecta cuantos más componentes añadamos). Esta gráfica muestra el resultado con sólo los seis primeros componentes.
Como evidencia el ejemplo, esa característica que mencionábamos en la cuerda de que todas las componentes tengan frecuencias múltiplos de una determinada, hace que contribuyan a modificar la forma del ciclo pero manteniendo su duración. Cambian la forma de onda final pero no su frecuencia ni periodo, y es un hecho tan común que merece su propio apartado. Apartado que aprovechamos para introducir los importantes conceptos de armónicos y parciales.
Armónicos y parciales, concepto del ‘fundamental’
[Índice]El sonido tan delgado y básico del diapasón, dista mucho de la riqueza, complejidad y contrastes que ofrecen otros muchos sonidos como el de la cuerda. La forma en la que vibran la inmensa mayoría de los objetos cotidianos es una superposición de diversos modos de vibración simples (sinusoidales) más tal vez agregado algún tipo de vibración aleatoria (no cíclica, para representar algún ruido que pueda estar presente).
Armónicos: En aquellos sonidos, como los de nuestra cuerda y de tantísimos instrumentos musicales, en los que hay un ciclo repetitivo somos capaces de percibir una sensación nítida de altura tonal (de ‘nota’) y se aprecia una mezcla de diversos modos de vibración cuyas frecuencias constituyen valores múltiplos de una frecuencia llamada fundamental. Por ejemplo, un violín produciendo la nota ‘La’ de la octava central (caracterizada por un ciclo que se repite con frecuencia de 440Hz) está generando la agregación de diversas componentes de vibración simple (sinusoidal) a 440Hz, 880Hz, 1320Hz, 1760Hz, etc., que llamamos armónicos. Se dice que el fundamental y esas componentes superiores forman una serie armónica. La resultante de combinar todos esos armónicos es una vibración cíclica con una forma de ciclo que no es ya de tipo seno, pero cuyo periodo es coincidente con el de dicho fundamental.
Parciales: En algunos otros casos (como en muchas campanas), se superponen varias formas de vibrar que de nuevo son aproximadamente sinusoidales, pero que no llegan a formar una serie armónica, sino que recaen en frecuencias distribuidas de forma que no son múltiplos de ninguna ‘frecuencia fundamental’ que pueda justificarlas a todas ellas. En esos casos estamos ante un sonido inarmónico, pero con una estructura todavía basada en combinación de modos simples de vibración periódica (sinusoidales), y que se percibe de una forma característica, que no es ni de una nota nítida ni de un ruido caótico. Al no formar una serie armónica, no cabe hablar de armónicos y tampoco tiene sentido el concepto de ‘fundamental’, y pasamos a denominarlos ‘parciales’. Los periodos y frecuencias de unos y otros parciales no están en este caso relacionados y tampoco se presenta un periodo característico en esa combinación.
Los armónicos y la serie armónica pasan a ser así un caso particular y especialmente organizado de este caso más general de parciales ubicados en posiciones cualesquiera.
Es la estructura y distribución de estos modos de vibración, de estos parciales (que habitualmente están configurados como un fundamental y sus armónicos), una clave principal para poder distinguir los diversos sonidos, instrumentos, y voces. Las vibraciones de tipo cíclico llevan aparejada una sensación nítida de altura tonal, de nota, y en ellos se aplica el concepto de serie armónica con un fundamental y diversos parciales. Las combinaciones inarmónicas de vibraciones simples no tienen una altura/nota tan definida, aunque se reconoce en ellas una ‘estructura’ interna que se manifiesta como combinación de parciales.
Si la vibración es rápidamente cambiante sin tono definido nin ningún otro tipo de regularidad ni parciales destacados, estamos ante un ruido (ruidos que pueden tener por supuesto interés como sonido y usos musicales). Pero comencemos por los sonidos en los que somos capaces de identificar una nota musical, un cierto tono (ya hablaremos de inarmonicidades y ruido en otro momento).
Diferencias de nivel entre parciales = diferentes formas de onda
[Índice]Si habéis jugado con algún instrumento de cuerda sabéis bien que al pulsar la cuerda a diferentes distancias de su extremo, suena completamente diferente. Según dónde actuemos sobre ella sonará de forma diferente porque ese punto de excitación es más hábil o menos para ‘activar’ cada una de las formas de vibración que soporta dentro de su serie armónica.
Si la excitamos (no es lo habitual) en el centro exacto de la cuerda (como muestra la opción ‘B’ de la siguiente figura), es el fundamental el modo que más generosamente puede moverse en esa posición y por tanto el que va a ‘quedarse’ con la mayor parte de la energía. Pero lo llamativo: podéis ver que los modos correspondientes a los parciales pares (el 2, 4, etc.) tienen en ese punto un ‘nulo’ de movimiento. Por tanto la energía entregada a la cuerda al percutir en el centro no es recibida por los parciales pares (ellos no ‘vibran’ en ese punto exacto), obtendríamos un sonido casi carente de esos armónicos (no del todo debido a efectos de segundo orden que afectan al movimiento de la cuerda).
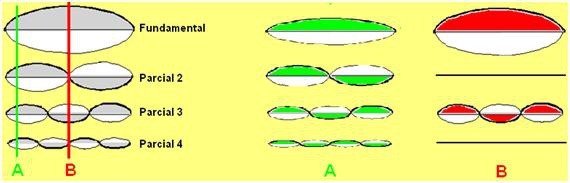
Es tipo de sonido que resultaría no es el que esperamos de la cuerda (de hecho sería más propio de un clarinete). Limitándonos a los muy primeros parciales ya se observa la tendencia en este caso a generar una onda de tipo ‘cuadrado’ más que rampa.
Entenderemos ahora porqué la actuación sobre las cuerdas (sea en guitarra, en violín o en piano) suele hacerse en otra posición ‘cercana’ a un extremo pero sin llegar ‘al borde’ (como en el punto ‘A’ de la figura). Vemos en la figura que en esa zona A es fácil obtener un patrón en el que todos los primeros armónicos están presentes y con un nivel cada uno de ellos inferior al anterior, con lo que se obtiene ese resultado ‘diente de sierra’ que mencionábamos antes.
La presencia de todos los primeros armónicos y ese carácter ‘decreciente’ de su nivel a medida que subimos por la serie armónica, es la que hace más rico, redondo y cálido el sonido que emana de la cuerda, y es por ello ese tipo de posición ‘A’ (y no la ‘B’) la más habitual para atacar las cuerdas.
Tampoco es habitual, salvo como efecto, excitar la cuerda muy cerca ya de su final, casi sobre el puente, porque en ese caso además de ser difícil poner en movimiento la cuerda y conseguir trasladar a ella suficiente energía, hay muy escasa diferencia entre el nivel de energía que reciben todos los primeros parciales, y eso hace que el sonido pierda cuerpo y solidez. Aquí tenéis el resultado de sumar los seis primeros parciales con amplitudes sólo un 10% más baja en cada uno respecto al anterior, que muestra una tendencia hacia forma de ‘pulso’ breve que sube y baja rápidamente en un tiempo corto permaneciendo el resto del ciclo en niveles bajos.
Los casos anteriores, derivados todos de una misma cuerda excitada en diferentes puntos, no son sino un ejemplo de cómo podemos generar diferencias de ‘timbre’, de ‘cualidad’ de sonido, jugando con los niveles relativos entre los diferentes parciales. Un ejemplo fácil de replicar. Cualquier guitarrista experimentado juega con esa posición en la que ataca al instrumento para obtener matices sonoros diferentes, unos más sólidos, otros más delgados o más nasales, etc., es decir, para obtener diferencias de timbre.
Fundamental como fundamento, no como principal
[Índice]En esta cuestión de las series armónicas hay que desterrar desde el principio un error común. Debido al nombre de ‘fundamental’ muchos consideran que el fundamental es aquel parcial que es más fuerte, el de mayor nivel y/o que es la primera (más grave) componente de las que presente la señal. En parecido error, muchos consideran que la frecuencia (y por tanto la nota o altura) que se oye en un sonido es la de su parcial más fuerte.
Pero no es así. Las series armónicas no necesitan estar completas e incluso el fundamental y los primeros armónicos pueden no estar presentes o ser muy débiles sin que eso afecte a la frecuencia conjunta resultante de la agregación.
El nombre de ‘fundamental’ tiene que ver con que la frecuencia de ese parcial es el ‘fundamento’, el origen, de todas las frecuencias que forman la serie armónica. Es posible, y se da con frecuencia, escuchar sonidos carentes de fundamental (en el sentido de que la energía en el fundamental no existe o ha desaparecido, con lo que sólo oímos armónicos). En esos casos nuestro oído es capaz perfectamente de reconocer la nota correcta (aquella a la que apunta ese fundamental inexistente) porque de hecho la combinación de los armónicos es tal que el periodo de la señal completa sigue siendo coincidente con el periodo del fundamental. Y siendo el periodo el mismo, aunque no esté presente el fundamental, la frecuencia del conjunto no varía y seguirá siendo la correspondiente al fundamental ausente. Es decir, el resto de los armónicos generan en su combinación una señal que se repite con la frecuencia del fundamental, a pesar de que dicho fundamental no esté presente.
Para ilustrarlo aquí tenéis un ejemplo. El resultado de sumar los seis primeros parciales con las mismas amplitudes que permitían generar el diente de sierra, pero anulando totalmente la presencia del fundamental, comparado con el resultado cuando sí está presente. Hay evidentemente una diferencia en la forma de onda, pero no en el periodo ni por tanto en la frecuencia que manifiesta la combinación, que sigue siendo la misma y que corresponde a la del fundamental.
Esta situación de que no sea el fundamental más fuerte que los armónicos es mucho más habitual de lo que podría pensarse. Muchos sonidos cotidianos son de ese tipo, sin ir más lejos es el caso de las vocales en el habla. De hecho podríais probar como ejercicio a grabar vuestra propia voz enunciando las 5 vocales y visualizar la forma de onda de cada una. Si lo hacéis conservad esa grabación. En próximas entregas la podremos volveremos a usar.
Una clasificación de los tipos de sonidos
[Índice]Pueden realizarse muchas clasificaciones de los sonidos. De momento vamos a interesarnos por una en la que distinguiremos
- Sonidos transitorios o impulsivos: sonidos que se desvanecen rápidamente, que no duran un tiempo extenso, y que no llegan a evidenciar una estructura interna estable.
- Sonidos estacionarios (estables), con tres variantes
- cíclicos o periódicos: con un ciclo básico que se repite idéntico a sí mismo o bien en evolución lenta, dando lugar la energía se concentre en determinadas frecuencias que forman una serie armónica
- inarmónicos (con energía concentrada en frecuencias concretas pero en posiciones no armónicas entre sí)
- aleatorios (con la energía no concentrada en frecuencias demasiado concretas, y por tanto sin repeticiones evidentes pero aún así con un sonido ‘estable’ en algunas de sus características; los solemos percibir como ruido, que puede tener distintos matices o colores)
De todos ellos encontraremos en la vida diaria, y normalmente aparecerán también combinados, de forma tal que de un sonido determinado podremos caracterizar una (o más) parte/s impulsiva/s, superpuesta a alguna componente cíclica, y también a alguna componente estable pero aperiódica. O puede haber un fenómeno inarmónico de corta longenidad en un sonido de mayor duración que acaba confluyendo a un patrón repetitivo. Esas y otras combinaciones son comunes.
Además muchas fuentes sonoras, como el habla, pueden considerarse como una sucesión de elementos transitorios y otros cuasiestacionarios. Las consonantes plosivas con claros transitorios impulsivos, la ‘f’ y la ‘s’ son ejemplos de sonidos de tipo ‘ruido aleatorio’, y las vocales son señales modelables como de tipo cíclico (aunque al articularse en una conversación están en constante evolución).
Pensad en una nota de clarinete. En el momento inicial podemos escuchar el ruido de las llaves que han sido movidas por los dedos (que es de tipo impulsivo) y durante el mantenimiento de la nota escucharemos tanto algún resto del ‘soplido’ (que no genera una sensación de nota, sino que es un ‘ruido’ aleatorio que acompaña al sonido principal) como el cuerpo principal de la nota producida por el instrumento, que es una señal de tipo periódico (p.ej. repitiendo su ciclo cada 440Hz si se trataba de la nota ‘La’ en la octava central).
Os propongo como actividad el que penséis otros ejemplos. Escuchad algunos sonidos (os recomiendo las grabaciones EBU-SQAM) y dedicad un tiempo a formar la escucha atenta. Buscad la asociación (no siempre trivial) entre lo que oís y lo que os representa la forma de onda en vuestro editor audio. Ved la forma de onda en su conjunto, y vedla en el detalle de un mayor zoom. Mirad cómo se transforma a medida que avanza un sonido. Algunos ejemplos de este tipo de actividad la tenéis en las lecturas y ejemplos que os propongo a continuación.
Más lecturas y ejemplos audibles
[Índice]No dejéis de completar este capítulo de hoy con estas otras lecturas que os indico (primeras entregas de nuestro curso de síntesis). No voy a reescribir lo que se cuenta en ellas, pero a todos los efectos serían parte también de este otro curso sobre acústica y electrónica:
Estructura armónica del sonido: esta entrega describe una parte de lo que hemos visto aquí hoy, pero además introduce el concepto de las resonancias en los instrumentos musicales, debidas a los efectos del cuerpo del instrumento, su caja de resonancia, etc. Leed con calma y preguntad allí lo que necesitéis.
Escucha de instrumentos acústicos: ejemplos sobre algunas imperfecciones respecto a la serie armónica que podemos encontrar en la realidad, y análisis del sonido de algunos instrumentos con sonidos reales (tomados de las grabaciones EBU-SQAM, de descarga gratuita, tenéis el enlace en ese texto).
Más allá de la serie armónica: a través de nuevos ejemplos mediante análisis de instrumentos reales y las grabaciones EBU-SQAM, apreciamos la presencia de irregularidades en el ataque/inicio de los sonidos, la presencia de ruidos añadidos a la serie armónica, sonidos con armónicos muy disjuntos (sin completar la serie) y los sonidos inarmónicos.
Y si además tenéis interés por los aspectos musicales, podéis repasar este otro texto sobre los conceptos musicales de consonancia y disonancia a la luz de la estructura armónica.



















