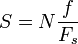Síntesis por Tabla de Onda o Wave Table
Este tipo de síntesis se concentra en los tipos de osciladores, siendo estos digitales, en el oscilador de un sinte wavetable (WT) en vez de tener una onda fija tienes una tabla de ondas, como el propio nombre indica. Esa tabla tiene una serie de casillas y en cada casilla hay una forma de onda de un solo ciclo. Luego puedes establecer cómo se va a reproducir esa tabla de ondas usando los moduladores disponibles en el sintetizador.
Una de las tantas formas es asignar un LFO al recorrido de las WT. En la matriz de modulación del sinte asignas un LFO con forma Seno para que module la posición en la tabla de ondas. Supongamos que tu tabla de ondas tiene 64 Casillas, entonces la cantidad de modulación que va aplicar el LFO la ajustas en 64 y así lo que tienes es que la tabla de ondas va sonar de principio a final. Si esa modulación la ajustas a un valor 2 solamente se reproducirían la 1era y la 2ª forma de onda.
Si la frecuencia del LFO la ajustas muy lenta la tabla de ondas se reproducirá lentamente y viceversa. La manera en que se va reproducir la tabla de ondas también variará según la forma de onda a la que sea ajustado el LFO.
Síntesis de tabla de ondas es una técnica de síntesis de sonido que emplea formas de onda periódicas en la producción de tonos musicales.
La técnica fue desarrollada por Wolfgang Palm, fundador y propietario de PPG (Palm Products GmbH) a finales de 1970 y se publicó en 1979, y desde entonces ha sido utilizado como el método de síntesis primaria en sintetizadores construidos por PPG y Waldorf Music además como un método de síntesis auxiliar por Sequential Circuits, Ensoniq , Korg , Access music y Dave Smith Instruments entre otros.
También se ha desarrollado de forma independiente por Michael Mcnabb en un plazo similar, y se utilizó en su obra clásica, "Dreamsong" (1977).
https://www.youtube.com/watch?v=bHGBkECBjvk
El primer sintetizador PPG en implementar este algoritmo fue el Wavecomputer 360, publicado en 1980 en dos versiones - la 360A, con 4 osciladores, y la 360B, con 8. Sin embargo, el sintetizador sonaba relativamente delgada, una consecuencia de tener sólo un oscilador por voz y la limitada típica polifonía de la mayoría de los sintetizadores de su era.
https://www.youtube.com/watch?v=eMsasn9Zokw
PPG pronto encontró el éxito con el lanzamiento del Wave2, que debutó en 1981, a un precio de alrededor de US $ 10.000 (GB £ 5,500). Contenía envolventes analógicos, LFO y filtros, con osciladores digitales. Dónde los sintetizador analógicos tradicionales sólo eran capaces de 5 o 6 formas de onda por oscilador, el PPG Wave 2 ofrece 30 "tablas de ondas" cada una con 64 formas de onda. Uno selecciona una tabla de ondas y luego una de las 64 formas de onda que contenía - un total de 1.920 formas de onda por oscilador disponible para su uso. En total, alrededor de 1.000 olas fueron fabricados entre 1981 y 1987 con dos cambios diferentes en el modelo (el PPG Wave 2.2, que añade más formas de onda y muestras, y el 2,3, lo que sumado multitimbricidad y MIDI), por lo que es el producto más exitoso de PPG fabricado. El PPG Wave también encontró un lugar en el escenario con artistas como A-ha , Alphaville , David Bowie , Geoff Downes , Electronic Dream Planet , Frankie Goes to Hollywood , Depeche Mode , Propaganda , Jean-Jacques Birgé , Jean Michel Jarre , Level 42 , Rush , Gary Numan , Missing Persons , Robert Palmer , The Stranglers , Talk Talk , Tangerine Dream , Tears For Fears ,Ultravox , Steve Winwood , Stevie Wonder , y muchos otros.
https://www.youtube.com/watch?v=izVH1CENIDs
https://www.youtube.com/watch?v=ySteoy-a8Hw
https://www.youtube.com/watch?v=5_hhZP4Mc_Q
Principio
La síntesis de tabla de ondas se basa fundamentalmente en la reproducción arbitraria y periódica de una forma de onda de un solo ciclo. En la síntesis de tabla de ondas, se emplea algún método para variar o modular la definición de forma de onda o evolución de la onda. Con 1 grado de modulación, esta forma de onda es una parte de una colección de una matriz de dos dimensiones. Moviéndose a lo largo de la otra dimensión de la matriz selecciona diferentes formas de onda. Un medio de interpolación (escalando y mezclando) entre las formas de onda adyacentes permite una transición suave de una forma de onda seleccionada a la siguiente. Si las formas de onda adyacentes contienen sutilmente diferentes armónicos (en magnitud y fase), la tabla puede ser barrido, de forma dinámica y sin problemas cambiando el timbre del sonido producido. Si las ondas adyacentes sin embargo, tienen radicalmente diferentes estructuras armónicas, el efecto escalera será notorio y estará presente debido a los rápidos cambios en el contenido armónico. Barriendo la tabla de ondas se realiza generalmente mediante el uso de un LFO o una rampa con la posición de inicio y la dirección de barrido está especificado por los parámetros de modulación, y el LFO o la velocidad de rampa de control de la velocidad del cambio armónico.
Dependiendo de los detalles de la implementación real, el sonido producido por la síntesis de tabla de ondas también puede contener objetos reconocibles, especialmente aliasing, cuantificacion y truncamiento de fase ruido.
Muchas tablas de ondas utilizadas en PPG y Ensoniq sintetizadores pueden simular los métodos utilizados por sintetizadores análogos, tales como la apertura y cierre de un filtro y barridos resonantes. A veces, una tabla de ondas se ha programado con un número de Banda eliminada ondas cuadradas de diferentes ciclos de trabajo. De esta manera, cuando se barre la tabla de ondas, que se traducirá en una idénticos, pero limitado en banda, forma de onda como con modulación de ancho de pulso (PWM) aplicada a una onda cuadrada.
Sintesis de Tabla de Ondas en Profundidad
Puede haber una situación o un deseo de escapar de las limitaciones o la complejidad de la definición de una forma de onda oscilatoria utilizando fórmulas matemáticas o segmentos de línea. Como se mencionó antes, esto podría ser una preocupación para la potencia de procesamiento, o simplemente el hecho de que sería más fácil para especificar la forma a través de una interfaz gráfica intuitiva. En casos como estos, músicos e ingenieros pueden utilizar tablas de onda para ser su oscilador de fuente. Tablas de ondas son populares en aplicaciones de síntesis digital, porque el acceso a un bloque de memoria es computacionalmente más rápido que el cálculo de los valores de uso de operaciones matemáticas.
La estructura básica de un oscilador de tabla de ondas:
[ Imagen no disponible ]
La tabla de ondas es en esencia un conjunto de N valores, con valores de 1 hasta N que representa todo un ciclo del oscilador. Cada valor representa una amplitud en un cierto punto en el ciclo. Tablas de ondas se muestran a menudo gráficamente con la opción para el usuario dibujar en la forma de onda que él o ella necesita, y como tal, representa una herramienta muy poderosa. También existe la posibilidad de cargar un pre-grabado forma de onda así; pero tenga en cuenta que un oscilador de tabla de ondas es sólo una tabla de referencia para un ciclo de una onda; no es lo mismo que unmuestreador. La tabla de ondas ha asociado un puntero de lectura que los ciclos a través de la mesa a la velocidad requerida y emite cada valor de amplitud en secuencia con el fin de recrear la forma de onda como un flujo de valores digitales. Cuando el puntero alcanza el último valor de la matriz de tabla, se restablecerá señalar uno y comenzar un nuevo ciclo.
Uso de tablas de ondas
El tamaño de la tabla de ondas y la frecuencia de muestreo del sistema a determinar cuál será la frecuencia fundamental del oscilador de tabla de ondas. Si tenemos una tabla de ondas con 1024valores individuales y una frecuencia de muestreo de 44,1 kHz, tomará:

segundo para completar un ciclo. Como se indica anteriormente, la frecuencia puede determinarse a partir , Que nos da una frecuencia fundamental de:

Hz.
Por lo tanto, resulta evidente que, con el fin de cambiar la frecuencia de nuestra oscilador debemos cambiar ya sea el tamaño de la tabla de ondas o la tasa de muestreo del sistema. Hay algunos problemas reales con los dos enfoques:
• Cambiar el tamaño de tabla de ondas significa cambiar a una tabla de ondas de tamaño diferente con el mismo, de forma de onda actualizada. Esto requeriría decenas, cientos o incluso miles de tablas de ondas individuales, uno para cada terreno de juego, lo que obviamente es totalmente ineficiente y la memoria que consumen.
• Los sistemas digitales, especialmente los mezcladores que combinan varias señales sintetizadas o grabadas, están diseñados para trabajar a una velocidad de muestreo fijo y hacer cambios repentinos de que es una vez más ineficiente y extremadamente difícil de programa.
• La frecuencia de muestreo requerido para reproducir las altas frecuencias con un nivel aceptable de precisión se vuelve muy alta y la pone alta demanda en el sistema.
Uno de los enfoques más prácticos y ampliamente utilizados a jugar un oscilador de tabla de ondas a diferentes frecuencias es cambiar el tamaño de los "pasos" que el puntero de lectura hace a través de la mesa. Al igual que con nuestro ejemplo anterior, nuestra tabla de ondas 1024-valor tenía una frecuencia fundamental de 43,5 Hz cuando se emite todos los puntos en la tabla. Ahora bien, si que entramos por la mesa de cada 5 valores, tendríamos:

Hz.
Se deduce de esto unas fórmulas generales para el cálculo del tamaño de paso requerida, S para una frecuencia dada, f:

Donde N es el tamaño de la tabla de ondas y es la frecuencia de muestreo. Es importante señalar que debido a que el tamaño de paso está siendo alterado, el puntero de lectura no puede aterrizar exactamente en el valor de la tabla definitiva N, y por lo que debe "wrap around" en la misma manera que las formas de onda generadas funcionalmente en la sección anterior. Esto puede hacerse restando el tamaño de la tabla desde el valor actual del puntero si excede de N; la forma algorítmica de los cuales puede ser fácilmente obtenida de los ejemplos anteriores.
Precisión de frecuencia y la interpolación
Debemos tener en cuenta que algunos valores de frecuencia pueden generar un tamaño de paso que tiene una parte fraccionaria; es decir, que no es un entero, pero un número racional. En este caso nos encontramos con que el puntero de lectura se trata de un paso a lugares de la matriz de tabla de ondas que no existen, ya que cada miembro de la matriz tiene un índice de valor entero. Puede haber un valor en la posición 50, pero ¿qué pasa con la posición 50,5? Si deseamos reproducir una frecuencia que utiliza un tamaño de paso fraccionario, hay que estudiar la manera de acomodar a ella:
• Truncamiento y redondeo. Mediante la eliminación de la fracción después del punto decimal se reduce el tamaño del paso a un entero-este es el truncamiento. Por ejemplo, 1,3 se convierte en 1, y 4,98 se convierte en 4. El redondeo es similar, pero elige el más cercano entero-3.49 se convierte en 3, y se convierte en 8,67 9. Para sencilla redondeo, si el valor después del punto decimal es inferior a 5, que redondear a la baja (truncamos), de lo contrario redondeamos hasta el siguiente número entero. El redondeo puede ser apoyado en el procesador sin costo, o se puede hacer mediante la adición de 0,5 al valor original y luego truncar a un entero. Para la síntesis de tabla de ondas, la única diferencia entre el truncamiento y redondeo es un desplazamiento de fase 0.5 muestra constante en la salida. Dado que no es detectable, y ni una mejora ni un detrimento-una decisión entre truncamiento y redondeo se reduce a lo que sea más conveniente o más rápido.
• La interpolación lineal. Este es el método de trazar una línea recta entre los dos valores enteros alrededor de la ubicación paso y utilizando los valores en ambos puntos para generar un valor de amplitud que interpola entre ellos. Este es un proceso computacionalmente más exigente, pero introduce una mayor precisión.
• Superior interpolación orden. Con interpolación lineal considerada primera interpolación orden (y truncamiento y redondeo considerado para la interpolación cero) hay muchas formas de orden superior que son de Hermite, Lagrange, y otros de uso común cúbicos. Así como interpolación lineal requiere dos puntos para el cálculo, órdenes superiores requieren incluso más puntos de tabla de ondas para ser utilizado en el cálculo, pero producen un resultado más exacto, inferior distorsión. Sinc interpolaciónpuede hacerse arbitrariamente cerca de perfecto, a expensas de la computación tiempo.
Al aumentar el tamaño de tabla de ondas, la precisión de los procesos anteriores se hace mayor y dará lugar a un ajuste más cerca de la, curva destinado idealizada.Naturalmente, los grandes tamaños de tabla de ondas resultan en mayores requerimientos de memoria. Algunos diseños de hardware del sintetizador de tabla de ondas prefieren tamaños de mesa que son potencias de dos (128, 256, 512, 1024, 2048, etc.), debido a los accesos directos que se aprovechan de la forma en que se construye memoria digital (binaria).
Bien mis agradecimientos A Nox, Soundprogramer y Arquitecto en Acero que se han tomado el tiempo a revisar y hacerme algunos comentarios.
en una proxima entrega algunos ejemplos.
Saludos




 Siento haber desaparecido, gente, sigo sin tener una buena época y tengo motivación cero últimamente.
Siento haber desaparecido, gente, sigo sin tener una buena época y tengo motivación cero últimamente.




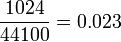
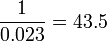 Hz.
Hz.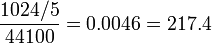 Hz.
Hz.