Sin animo de ofender ni faltar al respeto, tengo otra idea al respecto. Veamos: el cero existe, por lo tanto, puede , y debe haber instantes con señal cero. Luego, lo que manejan los bit, o mejor, el valor de las suma binaria de los bit en determinado instante, es un valor de voltaje, hasta un maximo estipulado. Veamos, si el maximo es un volt, una onda senoidal con valor pico de 1 volt, entregara 0,707 volt eficaces, o RMS, pero, a lo que voy, el bit mas significativo, debe dar medio volt, el siguiente, un cuarto, luego un octavo, y asi sucesivamente, jamas la suma supera a un volt, pero, se acerca cada vez mas , y aparte, las distintas combinaciones, hacen un numero cada vez mas preciso, cuantos mas bit haya: pero, es imprescindible que haya valores por arriba de cero, y por debajo de cero. O sea que se puede escuchar musica a 60 dB acusticos, o subir el amplificador arriba de 100, sin embargo, la cantidad de bit, determinara la precision de la reproduccion, a cualquier cantidad de dB. Aca me pregunto, para que se mide la suma de bit en dB?
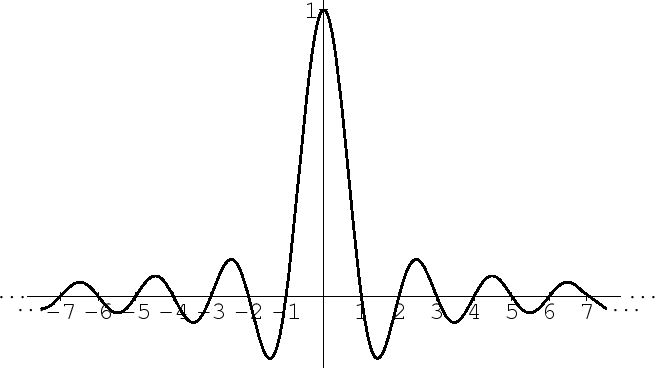
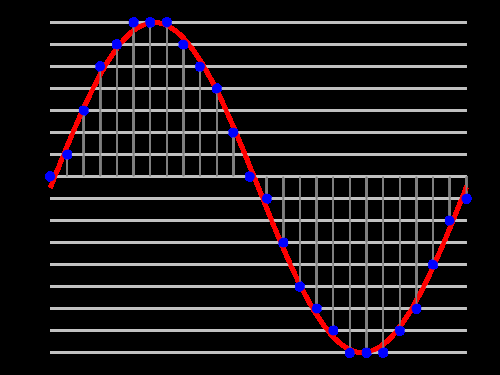
Me figuro una onda, compuesta de 44100 muestras por segundo, y a 16 bit de resolucion, y esa onda tiene 4000 Hz, entonces, cada semiciclo de la misma esta compuesta de solo 5 muestras, e imaginando algun armonico de esta, se me ocurre que debe dar un dibujo no demasiado preciso. De hecho, he leido comentarios de musicos que desaprueban el sonido del CD. Logicamente, que las limitaciones de un vinilo son aún mayores, aparte de introducir ruidos, wow, flutter, vibraciones, suciedad, desgaste, limitacion fisica , etc.
Basicamente, me pregunto porque con los avances que hay en materia digital, no avanza el tema alta fidelidad, si existe gente que puede gastar fortunas en equipo, si hasta se habla de cables especiales para parlantes, y antes, de tornamesas impagables, y de toda una parafernalia de chiches carisimos. Entiendo que la tecnologia esta disponible, pero para escuchar musica a 192 kHz y 24 bit, se la tiene que grabar uno mismo, y lo puede hacer con un aparatito de 100 dolares y la computadora, mas microfonos, claro
El tema, es que yo no quiero escucharme a mi, sino a Frank Sinatra, o al coro del ejercito de la URSS
Saludos