Nyquist, muestreo crítico y 96KHz

En un artículo publicado en Hispasonic en 2008 (https://www.hispasonic.com/reportajes/hay-vida-despues-20-khz/2466) Andrés Mayo abordaba la pregunta “¿Hay vida después de los 20 KHz?”, y ofrecía unos cuantos criterios y recomendaciones sobre la debatida existencia (y aún más debatida conveniencia) de registrar la actividad acústica que existe más allá del tradicional admitido límite humano de los 20 KHz. (que no es tal para otras especies con mayores aptitudes que la nuestra a ese respecto). No os diré su conclusión para animaros así a releer dicho artículo.

En estos debates sobre el uso de las frecuencias altas de muestreo siempre echo de menos algo que me parece esencial y que yo suelo denominar los problemas del ‘muestreo crítico’ y sobre todo los del ‘procesamiento’ de las señales digitales. De ahí mi interés por completar con otras consideraciones lo que ya contaba Andrés Mayo. Para no extender el artículo y no revisar de nuevo cosas ya tratadas por él, intentaré centrarme lo más posible en presentaros el ‘muestreo crítico’ y sus consecuencias.

Aquí por tanto la cuestión no es “¿Hay vida después de los 20 kHz?” sino más bien “¿La vida por debajo de 20 kHz recomienda/necesita las frecuencias altas de muestreo?”. Entre la ingeniería sesuda y la divulgación, favoreceré en la balanza esta última (sabiendo que los ‘sesudos’ entre vosotros podréis leer y completar entre líneas de las referencias más ligeras).

Vaya por delante que coincido globalmente con la razonable recomendación de mantenerse en 44,1 o 48 KHz. como frecuencia de muestreo que muchos han hecho ya en otras ocasiones en hispasonic. Sin embargo veréis que para algunas cuestiones y situaciones el uso de las velocidades altas es más que recomendable (sin que el objetivo sea necesariamente registrar la actividad por encima de 20KHz.). Y en todo caso, no está de más conocer los límites del mundo en el que nos movemos, porque siempre que nos preocupamos de ahondar en algo (aunque sea para verificar que estamos haciendo las cosas bien y no necesitamos cambiar en exceso nuestras costumbres) aprendemos por el camino.

El teorema de Nyquist (o del muestreo) nos asegura, con todo el halo de rigor de las matemáticas bien demostradas y plenamente asentadas, que para obtener una representación discreta (‘muestreada’) de cualquier señal basta con que la velocidad de muestreo (que solemos llamar fs, atendiendo a la denominación en inglés: sampling frequency) sea superior al doble de la máxima frecuencia que pueda presentar dicha señal. O a la inversa, basta con no intentar muestrear señales que oscilen más rápido que la mitad de fs.

Aplicado al audio, en el que asumimos que más allá de los 20KHz el oído humano no percibe los estímulos acústicos, esto significaría que bastaría usar frecuencias de muestreo superiores a los 40KHz para obtener una representación discreta que no pierda información, que no tenga ‘pérdidas’, que mantenga íntegra la calidad original, y que permita (cuando se desee) recuperar la señal acústica continua, indistinguible de la original.

Los 44,1 KHz. usados en el estándar de Compact Disc, o los 48KHz. usados en DAT y muchos entornos de vídeo serían por tanto más que suficientes velocidades de muestreo para garantizar la ‘perfección’ en la reproducción de audio.

Llegando al extremo, un tono de frecuencia fs/2 muestreado sólo ofrecería dos muestras por ciclo (una tomada de la parte positiva del ciclo, otra de la parte negativa), y por tanto resultaría en una alternancia de muestras:

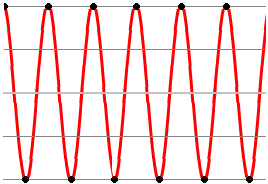
Pretender muestrear señales con componentes de frecuencias mayores a la mitad de fs genera insuficientes muestras para representar todas las alternancias que presenta la señal, con el conocido resultado del ‘aliasing’. Es por ello que en cualquier situación A/D, antes de realizar el muestreo se realiza un filtrado, que elimine suficientemente las posibles componentes cercanas o por encima de fs/2.

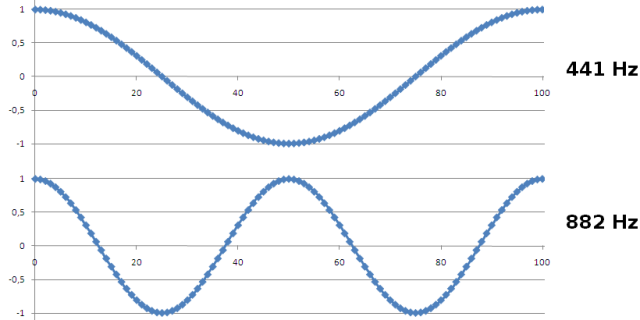
Pintemos las 100 primeras muestras (tomadas a fs=44,1KHz) de sendos tonos a 441 Hz, 882 Hz (doble del anterior). No hay mucho que objetar: las muestras sucesivas (incluso si la uniéramos con una línea como en los dibujos de los niños) trazan una curva que podemos reconocer con facilidad como senoidal (pinto cada muestra con un rombo para que las veaís con comodidad).

Solemos pensar que las matemáticas no admiten discusión. Y es cierto, pero sólo de forma ‘interna’ a las propias matemáticas. Cualquier conclusión matemática se deriva dentro de un ‘contexto’. Y el teorema de Nyquist tiene su propio contexto, que no podemos obviar.

• Asume un muestreo ‘perfectamente’ regular (sin jitter, etc.), cosa que razonablemente alcanzamos con la tecnología disponible a día de hoy, así que podemos obviarlo.

• Asume que el valor que se obtiene para cada muestra tiene infinita precisión, cuestión que no se da nunca en la digitalización de audio: llegamos a precisión de 16 o de 24 bits (o más), pero no infinita. Nuevamente, como no es el tema de este artículo, lo pasaremos por alto (dando por asumible el ruido remanente que resulte por esa discretización del valor de la señal).

• Asume que la señal original es de banda estrictamente limitada: no puede existir ninguna componente en ella por encima de la que correspondería a la mitad de la frecuencia de muestreo. Sobre esto volveremos enseguida, para presentar el ‘muestreo crítico’.

Pero sobre todo (y esto es lo que casi siempre olvidamos cuando hablamos de la frecuencia de muestreo y el teorema de Nyquist):

• Es un teorema que trata sobre la reconstrucción del audio original a partir de las muestras, pero no contempla la posibilidad (tan frecuente en nuestro caso) de que la señal sea procesada (modificada) tras el muestreo. Y es ahí donde quiero que reflexionemos un poco hoy.

Pero primero introduzcamos lo del ‘muestreo crítico’.

Pensemos ahora en un tono de 3528 Hz. Es ocho veces más veloz que 441Hz, pero aún lejos de los 22050Hz que corresponden a fs/2. A la vista de la figura, la cosa ya no resulta tan trivial como lo era con 441 y 882.

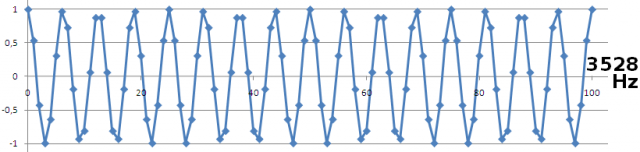
La unión ‘a ojo’ de los puntos genera una forma de onda que dista mucho de lo esperado. Aparecen ‘esquinas’ (inadmisibles en un seno); en algunos ciclos no se llega a mostrar la verdadera excursión total (entre +1 y -1); etc. En definitiva, ya no basta el unir ‘alegremente’ los puntos. ‘Parece’ una representación imprecisa, aunque sabemos (lo asegura el teorema de Nyquist) que sí es una representación ‘sin pérdidas’.

La aparente paradoja nos indica que acabamos de entrar en el reino del muestreo crítico. Cuando la velocidad de variación de la señal empieza a ser comparable a la velocidad de muestreo, la reconstrucción exige mucho cuidado para no introducir distorsión. Y eso que estamos hablando de 3528, ’todavía’ más de media docena de veces más pequeño que fs/2 (22050 Hz en nuestro caso).

Esto es lo que está pasando realmente: estamos tomando las muestras (puntos en azul) de la señal continua (en rojo)

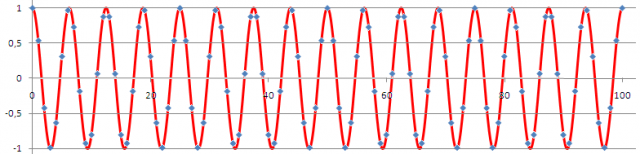
La reconstrucción, es decir, la recuperación de la exacta línea continua roja a partir sólo de los puntos azules es perfectamente demostrable (en el mundo ideal de las matemáticas en el que se mueve el teorema de Nyquist). Pero a costa de un sistema de reconstrucción que ya no es sencillo (no es ‘unir los puntos’).

Conseguir la reconstrucción correcta es la función que tiene asignada el filtro que siempre existe en cualquier convertidor digital a analógico: el filtro ‘suaviza’ las transiciones entre los impulsos representados por las muestras, y realiza una cierta ‘reconstrucción’.

Volvamos sobre el caso de una oscilación senoidal de frecuencia fs/2 que sea muestreada precisamente a velocidad fs:

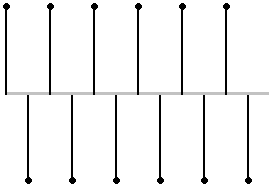
Algunos piensan que esta alternancia corresponde a una onda cuadrada, otros quieren ver en ella una triangular.

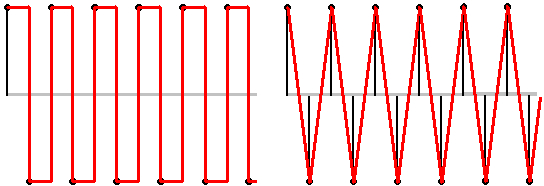
Ni una ni otra interpretación son correctas. Tanto la cuadrada como la triangular son formas de ondas con armónicos, y esos armónicos están muy por encima de fs/2. Son por tanto formas de onda ‘incompatibles’ con la premisa del muestreo sin aliasing.

Existe una única forma de onda estrictamente limitada a una frecuencia máxima fs/2 y que ofrezca esa alternancia de muestras, y es, claro, nuestro tono puro de frecuencia fs/2, que ya hemos visto antes:

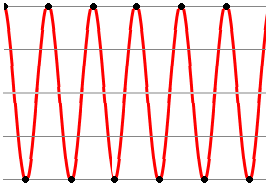
Lo que importa (y esto lo entiende cualquiera) es que la reconstrucción deja de ser ‘visible a ojo’ y exige inteligencia. Si la señal estaba correctamente muestreada (carecía de componentes por encima de fs/2) es imposible que tenga esos abruptos cambios que veíamos al reconstruir con líneas rectas. Esos contornos ‘picudos’ hablan de alta frecuencia, y excederían de fs/2. Están claramente alejados de las agradables y generosas redondeces de los senos (disculpad el desvarío por los calores del verano).

A la hora de ‘reconstruir’ debemos ser capaces de imaginar las curvaturas que corresponderían a no sobrepasar en la señal reconstruida en ningún caso variaciones más veloces que fs/2.

Cualquier cosa visible ‘a ojo’ es fácil de hacer y presentará pocos problemas, pero todo lo que exija ‘inteligencia’ (y ligar correctamente los puntos lo exige) implica (cara a los sistemas) complejidad y posibles problemas.

En los años 80, con los primeros samplers comerciales de precio relativamente asequible, un argumento que siempre se esgrimía desde los defensores de la superio calidad de los EMU (emulators, emax, y demás) era precisamente la calidad de su interpolación.
Pensad en un sampler. Cuando tiene que reproducir (a partir de una grabación de una nota determinada) otras notas, debe ‘recrear’ muestras de las que no dispone, a partir de aquellas que sí están en su memoria. Necesita obtener valores ‘intermedios’ entre cada dos muestras existentes (necesita ‘interpolar’). [Para los curiosos: varios samplers de la época usaban interpolación lineal, es decir, con líneas rectas uniendo los puntos, que sería lo mismo que la reconstrucción con ‘triángulo’ que he pintado antes; la interpolación ‘parabólica’ era usada en otros pero sigue sin ser un perfil como el que se obtiene con el interpolador ideal].

Concretamente la reconstrucción perfecta (tal como la promete el teorema de Nyquist) demanda el así llamado ‘interpolador ideal’: un filtro con respuesta impulsiva en forma de sinc (disculpad esta referencia excesivamente matemática, un guiño a los ingenieros –presentes o futuros- que anden leyendo esto). Os pinto la forma ‘sinc’, la respuesta impulsiva de ese filtro (sólo el fragmento ‘central’, se extendería a ambos lados):

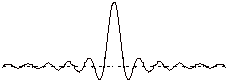
(básicamente sería una oscilación senoidal de frecuencia fs/2, pero que se amortigua hacia los extremos de forma inversamente proporcional a su distancia al centro)

Cualquier sistema tendrá que aproximar (y en función de la calidad de esa aproximación habrá mayor o menor calidad de la reconstrucción) la respuesta de tipo ‘sinc’. El filtro tipo ‘sinc’ tiene una respuesta impulsiva de duración infinita, y, aunque está concentrado, sus colas sólo caen a velocidad 1/x, es decir, caen con relativa lentitud.

Eso implica que para aproximarlo con cierta calidad se necesitarán filtros de respuesta que aunque no sea infinita sí sea larga (y por eso mismo costosa y compleja de implementar). Y estos filtros tendrán también un retardo largo de procesamiento, etc.

Aquí tenéis (para ahondar en lo difícil que puede resultar la interpolación correcta) las muestras de una señal de 15000 Hz y su correspondiente ‘original’. Unir bien los puntos resulta ya harto difícil.

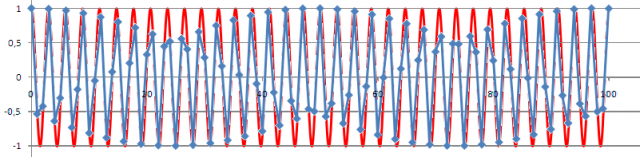
Sólo un filtro que sea muy cercano al ideal tendrá la ‘inteligencia’ (en realidad, la memoria) suficiente para poder realizar la reconstrucción con suficiente acierto. Y eso implica un filtro ‘largo’, cosa que muy pocas veces vamos a encontrar en la realidad.

Cualquier diferencia respecto al ‘ideal’ se puede valorar en términos de relación señal / ruido. Bastaría obtener la diferencia entre la señal original y la reconstruida (diferencia que consideraríamos como ‘ruido’ -aunque en rigor sería más propio considerarla como distorsión puesto que no es independiente de la propia señal-). Cuanto más recortemos las colas de la sinc (cuanto menos ‘ideal’ sea el filtro) tanto mayor será el ‘ruido’ que se generará acompañando la reconstrucción.

Así que, de momento, una conclusión (que por otra parte es bien conocida, y ya había sido comentada en cierta medida en el artículo de Andrés Mayo) es que por un problema ‘práctico’ de diseño de los filtros (tanto de los filtros ‘antialiasing’ que se aplican en la fase A/D para eliminar componentes superiores a fs/2, como de los filtros de reconstrucción a la salida de la fase D/A), podemos encontrar problemas que sólo evitando ir ‘al límite’ de lo que el teorema de Nyquist promete conseguiremos compensar.

Por eso en CD se usa 44,1 KHz (aunque las señales que se registran no superan los 20KHz) o en el DAT se optó por ir algo más allá (48KHz). A cambio de elevar la frecuencia de muestreo se hace menos crítico (un poco más relajado, un poco más económico) el diseño de los filtros.

Por eso, aunque vayáis a grabar en un sampler una señal que sepáis está limitada (por ejemplo) a 5Khz, no deberíais aplicar una frecuencia de muestreo de 10KHz, sino que haréis mejor en sobremuestrarla.

Pero importante como es esto, no es en absoluto de lo que quería hablaros, así que vamos ya al meollo de la cuestión que me motivaba para preparar este texto.

Pensad por un momento que el resultado de la fase A/D no es simplemente para ser registrado en un CD (u otro medio) y luego reproducido mediante D/A. Pensad que se trata de un audio que queremos procesar. Nos vale el ejemplo del sampler, pero vamos a algún caso aún más simple.

Da igual de qué proceso estéis hablando (salvo que se trate de algo como por ejemplo una distorsión instantánea -como la que sucede en un waveshaper-) todos conllevan memoria. Sólo reteniendo dentro del sistema un fragmento de la señal podremos (puede un sistema) tomar decisiones ‘inteligentes’ sobre ella para modificarla.

Pensemos en algo tan simple como por ejemplo un flanger o un chorus. ¿Sencillo, no? Tiene que obtener una versión ‘retardada’ de la señal original y combinarla con esta, pero además ese retardo debe ser variable. Un retardo variable implica que sólo ocasionalmente (solo para retardos que coincidan con un número entero de muestras) dispondremos del valor de la señal necesario entre las muestras disponibles en digital. La mayor parte de las veces necesitaremos obtener el valor que tendría la señal en un instante a medio camino entre dos muestras. Necesitaremos (nuevamente) ‘interpolar’ a partir de las muestras (que es lo único disponible) cuál sería el valor de la señal en un instante cualquiera entre dos muestras.

Es decir, volvemos a enfrentarnos (ahora desde la perspectiva del procesamiento) al problema de la ‘reconstrucción’ de la señal. Y basta ver el aspecto de la señal de 3528 Hz muestreada y la dificultad de su reconstrucción para intuir que no es una tarea fácil (no digamos ya la de 15000 Hz).

Que conste (vaya por delante) que soy un acérrimo defensor de lo digital en audio. Lo digo para que no os echéis encima de mí con lo que diré ahora (aunque como veréis abofeteo por igual a lo analógico y a lo digital).

Se suele achacar a los sistemas analógicos (yo mismo lo hago a menudo) que en ellos es inherente la presencia de ruido. Cualquier componente analógico introduce ruido. Y cuanto más complejo (más inteligente) es un sistema analógico, más componentes tiene y por tanto más fuentes de ruido que se acumulan. Hay una cierta ‘incompatibilidad’ de lo analógico con la complejidad.

Esto es asumido por muchos defensores de lo digital para reclamar la ‘superioridad’ de las tecnologías digitales. No he de negarlo, lo digital promete una mayor facilidad para alcanzar la complejidad sin tantas mermas, pero sí hay que ponerlo, nuevamente, en contexto. En la práctica, las soluciones digitales también sufren problemas. Al menos en el mundo digital existiría la vía teórica de aumentar la memoria, la capacidad de cómputo, etc. (o la frecuencia de muestreo, que es lo que nos ocupa hoy) para mejorar, pero esas vías de mejora no pueden extenderse sin límite en la práctica. Aunque la ‘teoría’ digital puede mostrase muy ‘limpia’ (tanto como las matemáticas) sus realizaciones prácticas a menudo no lo pueden ser tanto. Eso implica que no hemos de aplicar ‘ciegamente’ los brillantes resultados de la teoría, y en nuestro caso, que conviene reflexionar sobre si el muestreo en la práctica puede realizarse aplicando el criterio de Nyquist, o bien si necesitamos ‘defendernos’ de los problemas prácticos aplicando una buena dosis de sobremuestreo.

La figura que muestro a continuación indica qué relación S/N (señal/ruido) se obtiene al reconstruir un seno retardado partiendo de sus muestras y usando para la reconstrucción un filtro de tipo ‘sinc’ pero recortado a una duración finita. El error (la relación S/N) es mucho más grave cuando el retardo es precisamente de media muestra (lógico: es el punto intermedio y por tanto más alejado entre muestras disponibles).

La figura muestra el valor S/N en dBs para obtener retardo de 1 décima de muestra (hay una muestra relativamente cercana) y de 5 décimas (a distancia de media muestra, que es el caso peor). Y se ofrece el valor para diversas longitudes del filtro interpolador (aparecen resaltados los casos indicados en la figura como 10, 50, 100 y 200 que corresponden a usar para el cálculo 20, 100, 200 y 400 muestras –tomadas la mitad por delante y la mitad por detrás de instante que queremos ‘reconstruir’).

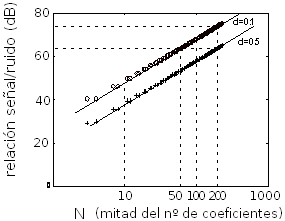
No os estoy dando el dato de cuál es la frecuencia del tono, pero tampoco es necesario precisarla. Lógicamente (como ya hemos visto) los tonos ‘lentos’ no tendrían mucho problema en la reconstrucción (no generarían excesivo ruido), mientras que cerca de fs/2 el ruido sería superior incluso a las cifras que ofrezco aquí. Esencialmente en la figura se trata de un tono que cae entre fs/8 y fs/4 (entre 5000 y 10000 Hz en nuestro caso, una franja en la que sí podemos esperar actividad audio significativa).

Fijaos que incluso con 400 coeficientes (que son muchos) el retardo de media muestra sólo logra una S/N algo superior a 60 dB, y ni siquiera para el retardo de una décima de muestra conseguimos que se acerque a los 80 dB. Pero esos 400 coeficientes no es algo que podáis esperar de casi ningún sistema. Generalmente trabajarán con duraciones de respuesta impulsiva bastante más cortas. Aparentemente estamos muy por debajo incluso de la calidad de CD y sus 96 dB S/N. El procesamiento (parecería) puede ‘ensuciar’ notablemente.

Y, lo siento, la situación no mejora ostensiblemente por pasar a usar diseños de filtros tipo IIR (que tienen sus propios problemas). Se trata de un problema ‘estructural’, de un dificultad inherente al hecho de que ‘inventarse’ (no es un verbo adecuado, se trata de ‘recuperar’) los valores intermedios, exige conocer muy bien el comportamiento de la señal, tener guardado un largo fragmento de ella y usarlo para ‘decidir’.

Además, en esto tendréis que ‘confiar’ un poco en mi palabra (para no seguir dilatando el artículo), creedme que cualquier procesamiento (no sólo un chorus o flanger, sino un ecualizador, un cambio de tono o un armonizador, un cambio de frecuencia de muestreo, y tantísimos otros) internamente está necesitado de obtener esas ‘interpolaciones’ que le permiten ‘imaginar’ cómo es la señal durante el tiempo que media entre dos de las muestras disponibles. Aunque trabajando realmente sobre las muestras, los procesos operan ‘virtualmente’ sobre la señal continua subyacente.

Antes de que disparéis las alarmas, pongamos lo que acabo de decir en contexto. La figura hablaba de cómo se ensucia un tono (en la región entre 5000 y 10000) al ser ‘procesado’ con un mero retardo que no use el interpolador ideal. Básicamente ese tono se vería acompañado de un ruido/distorsión que alcanzaría niveles sólo unas decenas de dB por debajo respecto a la señal deseada.

Pero pocas veces nuestras señales van a ser un único tono, o van a estar principalmente ocupando la zona alta del espectro audio. Pensad por ejemplo en este espectro (de un fragmento de una nota de saxo, que ya mostramos en otro artículo).

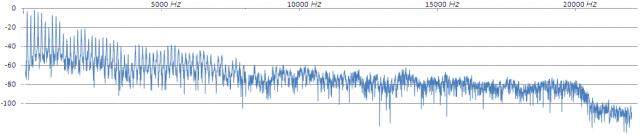
Las componentes que se encuentran por debajo de 1000 Hz (pensad en nuestros ejemplos de tonos de 441 y 882 Hz) apenas se ven afectadas por una interpolación pobre. Están tan sobremuestreadas usando fs=44,1KHz que casi cualquier interpolación o filtrado bastará.

Pensad ahora en las componentes que existen entre 2000 y 4000 Hz (ejemplificadas con el tono de 3528Hz). Ahí sí que habría que contar con procesos ‘cuidadosos’, un proceso básico empezará a afectar a esas bandas. Y desde luego, por encima, ya estamos en regiones de lo que denominaba ‘muestreo crítico’. Hay en ellas tan pocas muestras en cada ciclo, que para que los procesos puedan trabajar limpiamente necesitamos ‘extender’ a varios ciclos la duración del interpolador (o de cualquier otro proceso). Es decir, empezamos a necesitar que el proceso (ese chorus o esa ecualización a la que me refería) sea ‘de calidad’ (de una calidad tan refinada que casi nunca veréis en los productos).

Pero nuestras señales (como la del saxo) son en realidad agregación de muchas componentes. De forma sólo esquemática (no está calculado con cifras reales, es sólo para ofreceros una representación de la idea), pensad que, con unos procesamientos de una calidad (nº de coeficientes) razonable, en la zona cercana a fs/2 (a los 22050Hz) hay tanto ruido como señal, que a 10000 Hz podemos estar en un ruido 40 dB por debajo de la señal, y que a medida que descendemos en frecuencia la distancia entre la señal y el ruido generado en su procesamiento crece exponencialmente (hasta llegar a un ruido despreciable en frecuencias del registro grave). Pinto sobre el espectro anterior unos pocos puntos de este tipo como ‘referencia’: en verde el nivel que tenemos de señal y en rojo un posible nivel de ruido generado.

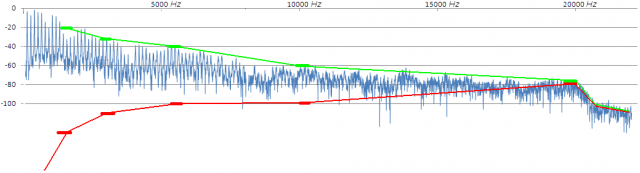
El resultado ‘agregado’ estaría dominado por el hecho de que la mayor parte de la energía de este sonido está en la región de los primeros armónicos, una región en la que hay menor ‘sensibilidad’ al procesamiento (el ruido está muy por debajo de la señal).

Incluso considerando que nuestro oído opera ‘por bandas’ y que los fenómenos de enmascaramiento actúan individualmente en cada una de las regiones espectrales, no parece que nos debamos preocupar mucho. Afortunadamente la relación señal a ruido se empobrece tanto más cuanto más alta es la frecuencia, y nuestras señales musicales suelen ser ‘al revés’ menos energía cuanta mayor es la frecuencia, con lo que el pedestal final de ruido agregado en altas frecuencias será de niveles muy pobres (y en esas frecuencias la peor sensibilidad de nuestro oído reclamaría mayores niveles).

Aún así, entenderemos ahora mejor la conveniencia de no forzar el aprovechamiento de lo que promete el teorema de Nyquist. Usar 44,1 KHz para registrar señales limitadas a 20KHz, o aún mejor los 48KHz son actuaciones que podemos comprender.

Podemos comprender ahora también porqué suele darse la recomendación de grabar a una frecuencia que coincida con (o sea múltiplo) la frecuencia a la que vayamos a generar el producto final. Si se trata de un CD, grabar a 44,1KHz (o a 88,2) en lugar de a 48 o 96 permitirá que no haya que ‘reconvertir’ la mezcla final desde los 48 a los 44,1. En esa reconversión de nuevo nos enfrentamos a la necesidad de ‘recrear’ valores para los que carecemos de muestra (necesitando por tanto la interpolación).

Comprendemos también porqué, si llega el caso de que necesitemos hacer estas conversiones (u otros procesos) puede ser conveniente no aplicar versiones de software que actúe en tiempo real, sino versiones con mayor demanda de computación aunque impliquen dejar el ordenador calculando el resultado del proceso para poderlo obtener más tarde. Por volver sobre nuestros ejemplos, esas versiones de ‘alta calidad’ (y a veces a cambio fuera de tiempo real o al alcance sólo de centros de ‘mastering’ especializados) están aplicando procesos con un alto número de coeficientes (u otras formas de ‘complejidad’) y por tanto con una mejor defensa frente a los problemas.

Como en los dibujos animados: no se vayan todavía, aún hay más. Pensad ahora en otros tipos de sonidos y músicas. Aquí tenéis una gráfica que muestra el espectro de un glockenspiel (que ya he usado en uno de los artículos sobre síntesis).

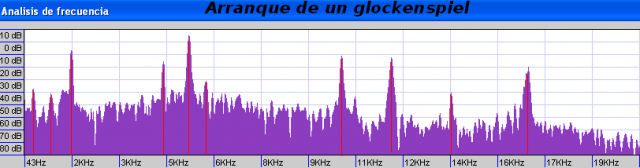
Pensad en el procesamiento de este sonido en los términos que venimos discutiendo. Sin duda en este caso vamos a estar mucho más expuestos a que las ‘deficiencias’ prácticas del procesamiento se manifiesten de forma detectable, perceptible.

Pensad en el caso de una pista de triángulo (el instrumento de percusión), o pensad en música experimental y electroacústica, en la que a menudo subvertimos el orden natural y nos inventamos fuentes sonoras atípicas. El ‘muestreo crítico’ al que vamos a someter a estas señales, puede complicarnos la vida en el momento en que queramos procesarlas.

¿Estamos ante un túnel sin salida? Pues bien, precisamente aquí es donde quería apoyar la utilidad de acudir a velocidades altas de muestreo, si bien sólo para el caso de material sonoro ‘crítico’.

Como la figura anterior muestra, la relación S/N sufre mucho justo en el retardo de ‘media muestra’. Cuando pasamos de fs 48 KHz a fs 96 KHz estamos permitiendo a todos nuestros procesadores y efectos disponer del valor más deseado (el más difícil): el que cae ‘a mitad’ de dos muestras. A 96Khz los nuevos valores ‘más deconocidos’ pasan a ser los que estaban a 0,25 muestras de alguna de las que ya estaba disponible. Los nuevos ‘grandes desconocidos’ resultan ahora ser aquellos puntos que en la versión de 48KHz estaban a 0,25 muestras de distancia.

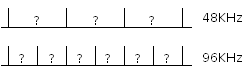
Incluso si no nos importa lo que pueda existir más allá de los 20KHz en el audio (sea porque no lo oímos, sea porque usamos micrófonos y sistemas de grabación que tienen sus propias limitaciones de banda), el registrarlos a una tasa de muestreo rotundamente superior al mínimo establecido por el teorema de Nyquist ofrece una oportunidad para obtener un mejor rendimiento de los sistemas de procesamiento, que encontrarán una señal más ‘detallada’ sobre la que trabajar. Dicho en plata, puede tener sentido grabar a 96 material que sabemos está limitado a 20KHz si en él intuimos que va a haber una presencia importante de señales ‘críticas’ y vamos a necesitar procesarlas.

No se trata pues sólo de evitar los fenómenos de ‘aliasing’ y semejantes asociados al ‘codo’ o límite fs/2, sino de obtener un mejor comportamiento de los procesos que realicemos en el audio, evitando que los ruidos/distorsiones debidos a los límites prácticos del procesamiento se manifiesten.

Eso sí: es necesario que la señal sea digitalizada en la velocidad alta en origen. Usar un proceso a 96KHz sobre una señal muestreada a 48KHz generalmente significa que el proceso está precalculando una versión a 96KHz para procesarla. Y ese precálculo pocas veces será óptimo (introducirá su propio ruido/distorsión) y por tanto puede dar al traste con el pretendido beneficio (salvo que nos aseguremos de optar por un ‘upsampling’ de alta calidad, que quizá exija procesado fuera de tiempo real). [Por cierto, pensad al respecto cuando integráis grabaciones y sonidos capturados con diferentes velocidades de muestreo dentro de un proyecto: puede ser conveniente adecuarlas a la nueva velocidad de muestreo en un software específico y no con las opciones -a menudo básicas- de autoconversión durante la importación]

Por el contrario, si hemos capturado la señal a 96KHz (o podemos permitirnos –quizá en un entorno ‘off line’ obtener su versión remuestreada a 96 con garantía de calidad-) entonces puede tener interés y sentido el tratamiento a 96KHz. No para el día a día, pero sí en proyectos o situaciones críticas que lo demanden.

No puede haber una moraleja final, o al menos no una simple. Pero espero que hayáis disfrutado y reflexionado algo por el camino, pues eso (más que las recetas) es lo que deja fruto.

En función del tipo de señal que estemos tratando, podremos a veces encontrar que los trucos y procesos que siempre han sido aliados nuestros y funcionaban correctamente, empiezan a flaquear. Tener la capacidad de reaccionar y diagnosticar es lo que nos corresponde. Y un recurso que en ocasiones puede ser útil es el de ampliar la calidad del procesamiento (en algunos entornos el usuario puede escoger entre distintas longitudes de respuesta de filtros, por ejemplo) o alternativamente grabar en origen a una fs alta (o bien realizar un proceso de upsampling de alta calidad para después aplicar los procesos en la nueva velocidad).

Y al menos, dado que como veis no hay magia (ya sea por aumentar el número de coeficientes o por aumentar la tasa de muestreo, en ambos casos estamos aumentando la complejidad computacional), sí tenemos un criterio más para intentar dilucidar porqué en algunas ocasiones nos encontramos con determinados resultados más pobres (acompañados de ruido o distorsión) de lo esperado.