Síntesis (1): estructura armónica del sonido

Arrancamos lo que será una extensa serie dedicada a la síntesis en sus distintas variantes. Pero antes de comenzar propiamente con la síntesis, resulta ineludible contar con un mínimo de conocimientos sobre la materia base con la que construimos la música: el sonido.

El sonido es un hecho físico y necesitaremos conocer algunas reglas físicas y matemáticas (afortunadamente sencillas). Hoy abordaremos la estructura armónica de los sonidos musicales, el modelo excitador+resonador (base de la síntesis sustractiva entre otras).

Muchos conoceréis ya estos conceptos de hoy, pero pretendo que la serie pueda reunirnos a todos y para ello también tenemos que atender a los más recién llegados al mundo de la síntesis. En otras ocasiones acudiremos a temas más específicos. En todo caso, confío en que en todas las entregas os encontréis a gusto leyendo y con oportunidades para aprender o reflexionar, sea cual sea vuestro bagaje inicial, novel o ya iniciado.

Como es bien sabido, el sonido proviene de aquellas vibraciones transmitidas a través del aire y capaces de dar lugar a una sensación auditiva (cuando cumplen determinados requisitos de frecuencia, intensidad, etc.). Estas vibraciones pueden presentar caracteres muy diferentes. Así, la vibración que tiene lugar en un diapasón es prácticamente un tono puro o una vibración armónica simple (o senoidal, por usar un término más matemático) mientras que para cualquier instrumento musical la vibración no es nunca simple sino una mezcla de diversas formas de vibración (que llamamos parciales) cuyas frecuencias constituyen habitualmente valores múltiplos de una frecuencia llamada fundamental (en cuyo caso los parciales se denominan 'armónicos' y forman una 'serie armónica'). Es la estructura y distribución de estos modos de vibración una clave principal para poder distinguir los diversos instrumentos, voces y ruidos (y por tanto para sintetizar). Si la vibración es rápidamente cambiante sin tono definido, estamos ante un ruido (ruidos que, porqué no, pueden tener por supuesto usos musicales). Pero nuestro interés aquí y hoy se centra en los sonidos en los que somos capaces de identificar una nota musical, un cierto tono (ya hablaremos de ruido otro día).

Sabemos, p. ej., que la nota La central se suele afinar a 440 Hz. (Hertzios, una unidad que mide cuantas veces por segundo se completa el ciclo de vibración). En el caso de un diapasón, esencialmente oímos casi una única vibración pura, una vibración sinusoidal. Las láminas de ese diapasón vibran 440 veces por segundo. Decimos que la frecuencia de vibración de ese diapasón ha sido ajustada a 440 Hz.

Sin embargo los sonidos de la mayoría de los instrumentos musicales cuando interpretan notas no son una única vibración pura sinusoidal. Estos sonidos, como decíamos, son resultado de la superposición de varios modos de vibración que ocurren simultáneamente en el instrumento y que guardan una relación precisa entre ellos: son armónicos entre sí. Lo que quiere decir que las frecuencias de los distintos modos son múltiplo de una de ellas (la del más grave, que llamamos ‘fundamental’). Así cuando percutimos una cuerda para que suene ese La, dicha cuerda vibrará (y por tanto sonará) a 440 Hz., pero también a 880Hz., 1320 Hz., etc. (los sucesivos múltiplos de 440). Puede parecer extraño (al fin y al cabo difícilmente apreciamos con la vista el detalle de la vibración de la cuerda) pero es un hecho físico que en esa vibración compleja se superponen muchos modos diferentes de vibración simple relacionados armónicamente (y se puede comprobar mediante múltiples experimentos sencillos).

No con ánimo de demostrar nada, sino sólo de ilustrar, pensemos por ejemplo en una cuerda percutida: oscila en toda su longitud con una frecuencia que depende de la longitud y rigidez de la cuerda, pero además cuando la percutimos también oscila en un segundo modo el doble de rápido en el que una mitad de la cuerda sube mientras la otra mitad baja, y un tercer modo, etc. Cada uno de estos armónicos es de menor nivel (menos intensidad) que el anterior. El movimiento final de la cuerda es el resultado combinado de todos estos modos de vibración y así también el sonido que resulta contiene esos diferentes armónicos a los que nos referíamos.

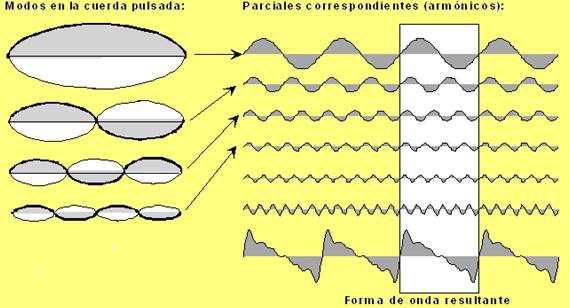
En definitiva el sonido de la cuerda (igual sucedería con cualquier otro elemento musical u objeto acústico) es ‘complejo’ (compuesto) de varias vibraciones sinusoidales superpuestas. El ciclo básico, la forma de onda resultante, el sonido que podemos escuchar o grabar, es la suma de esas diversas componentes.

Por cierto, habréis observado que se asemeja la forma de onda obtenida para la cuerda pulsada a un diente de sierra (que es una forma de onda habitual en los osciladores de los sintes precisamente como base para construir, entre otros, los sonidos de cuerdas).

Si habéis jugado con algún instrumento de cuerda sabéis bien que al excitarla a diferentes distancias de su extremo, suena completamente diferente. La cuerda está esperando que la excitemos para ponerse a vibrar. Según dónde actuemos sobre ella sonará de forma diferente porque ese punto de excitación es más hábil o menos para ‘activar’ algunas de las formas de vibración que la cuerda soporta.

Si la excitamos (no es lo habitual) en el centro exacto de la cuerda (como muestra la opción ‘B’ de la siguiente figura), es el fundamental el modo que más generosamente puede moverse en esa posición y por tanto el que va a ‘quedarse’ con la mayor parte de la energía. Pero lo llamativo: podéis ver que los modos correspondientes a los parciales pares (el 2, 4, etc.) tienen en ese punto un ‘nulo’ de movimiento. Por tanto la energía entregada a la cuerda al percutir en el centro no es recibida por los parciales pares (ellos no ‘vibran’ en ese punto exacto), obtendríamos un sonido casi carente de esos armónicos (no del todo debido a efectos de segundo orden que afectan al movimiento de la cuerda).

Entenderemos ahora porqué la actuación sobre las cuerdas (tanto en guitarra, como violín como piano) suele hacerse en otra posición ‘cercana’ a un extremo sin llegar ‘al borde’ (como en el punto ‘A’ de la figura). Vemos en la figura que en esa zona es fácil obtener un patrón como el que mostrábamos en la figura anterior: todos los primeros armónicos están presentes y con un nivel cada uno de ellos inferior al anterior (con lo que se obtiene ese resultado ‘diente de sierra’ que mencionábamos antes).

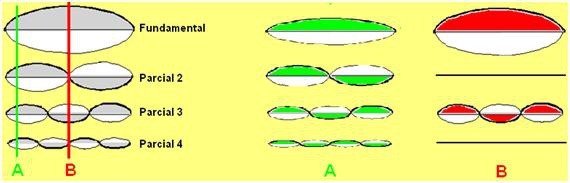
La presencia de todos los primeros armónicos y ese carácter ‘decreciente’ de su nivel a medida que subimos por la serie armónica, es la que hace más rico, redondo y cálido el sonido que emana de la cuerda, y es por ello ese tipo de posición ‘A’ (y no la ‘B’) la más habitual para atacar las cuerdas.

Lo que acabamos de comentar y representar se refiere a una cuerda suspendida ‘en el aire’, sin estar asociada al cuerpo de ningún instrumento. Pero, continuando con el ejemplo, en realidad las cuerdas aparecen en los instrumentos musicales asociadas a una ‘caja de resonancia’ (pensad en un violín, una guitarra, etc.).

La cuerda transmite buena parte de la energía de su movimiento a esa caja a la que se encuentra unida. La caja se ve sometida (a través de la unión con la cuerda) a los esfuerzos y tensiones que causa la cuerda y entra también en vibración. Eso permite que la caja actúe como ‘radiador’ o ‘difusor’ del sonido que originalmente se produce en la cuerda.

La caja tiene un efecto no neutro. Lo que suena en presencia del cuerpo, no es un reflejo fiel de lo que sucede en la cuerda ‘libre’ (ese diente de sierra al que antes me refería). Cualquier objeto, y en especial esos cuerpos de los instrumentos musicales, tienen mayor o menor ‘facilidad’ para entrar en vibración en cada una de las regiones del espectro de audio. Esa mayor o menor facilidad de la caja para radiar las diferentes componentes de vibración de la cuerda pulsada se traduce en que las amplitudes de esos armónicos van a verse variadas. Algunos parciales quedarán reforzados comparativamente con los demás.

Además de esa transmisión directa de la vibración está también (en instrumentos como la guitarra, en los que el agujero bajo las cuerdas permite que el aire desplazado por ellas alcance el interior de la caja) el efecto que el cuerpo causa como mero ‘entorno’ acústico de la cuerda (el aire rebota dentro de las paredes de la caja, transmite energía a la propia caja y también se vé afectado por las reflexiones en la propia caja).

Al final, se trata por tanto de una ‘respuesta en frecuencia’ que la caja de resonancia impone sobre el sonido que emana originalmente de la cuerda.

¿A qué os recuerda esto? A los filtros de los sintetizadores sustractivos. El oscilador, generando un diente de sierra, en esencia asume el papel de la cuerda ‘libre’, pero al pasarla por un filtro (o mejor un par de ellos, sino más) podemos eliminar ciertas frecuencias, realzar unas frente a otras, etc. Un sinte básico sólo tiene filtro ‘paso bajo’, pero un sinte más rico contará con filtros paso bajo, paso alto, paso banda, de ‘peaking’, ‘notchs’, de ‘formantes’, u otras variantes. Cuando pasamos el sonido del oscilador (el diente de sierra en nuestro ejemplo) por un filtro (o un conjunto de filtros) estamos simulando el efecto del cuerpo resonante del instrumento, que modifica el balance de unos armónicos frente a otros.

El grado de esa modificación es muy alto en muchos instrumentos acústicos. Hay numerosos experimentos que demuestran y hacen visible (e incuso permiten medir) la realidad de la existencia de esa ‘respuesta en frecuencia’. Los dos más habituales son el método de Chladni (que podríamos incluso experimentar a título personal sin grandes medios) y la interferometría (que exige ya un equipamiento muy específico). Si buscáis en Internet por esos dos términos encontraréis numerosas referencias e imágenes (por cierto este tipo de imágenes son útiles para saber por dónde se está radiando cada armónico, y poder así hacer una colocación ‘inteligente’ de los micrófonos aprovechando la ‘ecualización acústica/espacial’ que nos ofrece la propia caja).

En estas imágenes que os muestro (tomadas de http://www.bbc.co.uk/news/science-environment-13573631) veis el patrón de radiación de los tres primeros armónicos de una guitarra (y podéis apreciar, de forma parecida a lo que os contaba de la cuerda, como en este caso la superficie de la tapa se subdivide en 2, 3, etc. secciones a la hora de producir los armónicos).

En realidad cualquier lutier usa una técnica más sencilla para comprobar como ‘suenan’ las piezas de madera destinadas a la caja (o bien esta al ensamblarla): da un golpe seco sobre la caja y ‘oye’ como suena. Como resultado de ese golpe se oye un sonido ‘coloreado’ de acuerdo a qué frecuencias transmite mejor/peor la caja (en términos técnicos está obtenido la respuesta impulsiva de la caja) y llegado el caso podría decidir (con su experiencia) adelgazar alguna parte antes de ensamblarla o encolar alguna varilla, para modificar la respuesta.

El efecto de estos ‘resonadores’ es muy destacado (en términos de ingeniería ese filtrado acústico a menudo es de un orden elevado y con una gran selectividad, lo veremos en un ejemplo enseguida). Todos podemos comprobarlo: si introducimos un altavoz por el agujero de una guitarra, todo lo que hagamos sonar por él se verá muy fuertemente coloreado por estar sucediendo ‘dentro’ de la caja.

Resumiendo lo presentado hasta ahora, en los instrumentos musicales encontraremos un elemento ‘productor’ de vibración (la cuerda en el ejemplo) y otro elemento (el cuerpo / caja del instrumento) que modifica la forma en que suena por sí mismo ese productor introduciendo realces significativos de una gamas de frecuencias respecto a otras, imponiendo determinados picos y valles en ciertas frecuencias y estableciendo así un patrón de resonancias, una ‘respuesta en frecuencia’).

Es esta una forma bastante habitual de concebir el sonido de los instrumentos musicales cara a la síntesis: dos partes, el elemento vibrador y el elemento resonador. Ya hemos anticipado que en síntesis analógica esto lleva al modelo oscilador+filtros.

Esas diferentes frecuencias de vibración que se producen combinadas en el ‘vibrador’, se pueden representar en el así llamado ‘espectro’, en el que se indica la amplitud o intensidad de cada una de las oscilaciones básicas (que tienen una relación armónica entre ellas: todas las frecuencias son múltiplos de una que se llama fundamental y que define la nota generada por la cuerda). El espectro representa la amplitud de cada componente frente a su frecuencia. En un caso como el de la cuerda que nos sirve de ejemplo (cada armónico menos intenso a medida que subimos en frecuencia) podría ser semejante a esto:

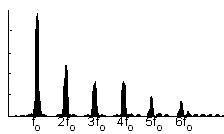
La figura es el espectro de una cuerda pulsada real. Se observa la concentración de la energía en ciertas frecuencias relacionadas armónicamente, que hace patente la estructura armónica del sonido.

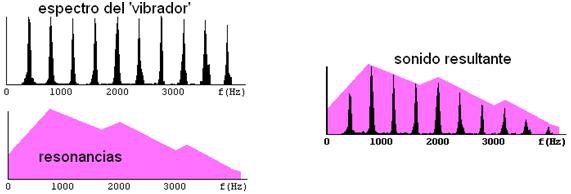
Para la siguiente gráfica he partido de una nota de violín (ya interviene el cuerpo del instrumento). En la ejecución de esta nota concreta se observa una fuerte (aunque no extrema) concentración de energía sobre un armónico (no sobre el fundamental), debida a una resonancia muy destacada en el cuerpo del violín que se empleó para producir la nota. Dado que aún hay bastante energía sobre otros armónicos (aunque muy repartida en pequeñas contribuciones sobre cada uno de ellos) nuestro oído no sería engañado y percibiría la nota adecuada en su octava correcta, pese a que haya un armónico con mayor intensidad que el propio fundamental (incluso en la forma de onda se puede apreciar el verdadero periodo de repetición, pese a que a primera vista dominan las oscilaciones causadas por ese armónico más fuerte).

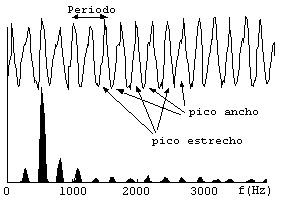
En este sonido podemos reconstruir el proceso por el que el sonido producido por el elemento vibrador (cuerda) se modifica en el resonador (cuerpo) configurándose así el sonido final que percibimos en la escucha del instrumento:

Cuando interpretáramos otra nota, las rayas armónicas guardarán entre sí una distancia diferente, pero las resonancias esencialmente no se modifican (la caja es fija, lo único que hemos podido variar es la longitud de la cuerda vibrante). Aquí teneís una ‘recreación’ de qué sucedería una octava por encima:

Vemos ya en estos dos ejemplos notables diferencias en el espectro (la distribución de energía en los diferentes armónicos): en uno continuamente decreciente, en otro sometido a una extraordinariamente fuerte resonancia (que sin embargo no lleva a engañarnos sobre el verdadero ‘fundamental’ de la colección de armónicos, que nunca está definido por aquel que sea más fuerte, sino por aquel que podría actuar como origen de la serie).

El espectro distingue unos sonidos de otros, está relacionado con la cualidad musical del ‘timbre’. De hecho, nuestro oído (gracias a la cóclea), realiza físicamente este análisis espectral. Nuestro oído obtiene una representación semejante al espectro de las señales escuchadas, y es esta representación la que se eleva por el nervio auditivo hacia instancias superiores cerebrales para su análisis. El espectro de cada instrumento es distinto y nos permite reconocerlos y diferenciarlos.

Tal como vemos el sonido resultante depende tanto del elemento productor de la vibración inicial como del elemento ‘resonador’. Y es más: el espectro de un mismo instrumento cambia notablemente según qué notas toque: permanece la ‘envolvente espectral’ (que he mostrado en morado) y nuestro oído detecta esa presencia y permanencia de determinadas resonancias que le permiten reconocer esas notas (tan distintas) como pertenecientes a un mismo instrumento.

Muestro ahora otro ejemplo de espectro sobre otra familia de instrumento (así salimos de las cuerdas y veremos cómo también el ‘excitador’ determina el timbre resultante). En esta otra figura (a partir de una nota de trompeta) vemos la forma de onda (el sonido tal como lo recogería un micrófono o lo mostraría un osciloscopio) y el correspondiente espectro. Muestra un sonido rico en armónicos, todos de amplitud considerable. Un espectro claramente diferente al que vimos para la cuerda anterior.

En la boquilla de la trompeta hay una constante pelea entre la presión del aire que insufla el músico y la ‘puerta cerrada’ que son sus labios. Cerrad los labios e intentad soplar (o mejor todavía, poned la mano delante -a modo de ‘embocadura’- y realizad una ‘pedorreta’), notaréis que crece la presión hasta que (repentinamente) se libera y sale un ‘golpe’ de aire. Esa liberación brusca de la presión permite que los labios vuelvan a sellarse y comienza el ciclo. Claramente es un efecto ‘impulsivo’, nada que ver con la vibración que nos daban un diapasón o una cuerda (y que era un movimiento suave, contínuo).

¿Habéis visto la forma de onda? Es precisamente una sucesión de ‘pulsos estrechos’ Un pulso estrecho es una de las formas de onda habituales también en sintetizadores, para poder obtener sonidos de viento metal entre otros. El espectro de un pulso estrecho (si hubiéramos capturado el sonido de los exabruptos de aire justo a la salida de los labios) es tal que todos los armónicos (hasta un orden muy alto) tienen prácticamente la misma intensidad. En la figura anterior, veréis que en el espectro no todos los picos son de altura ‘idéntica’ porque está también el efecto de las resonancias en el tubo y en la campana.

Aunque los ejemplos mostrados hasta el momento únicamente han estudiado los sonidos desde un punto de vista 'estático', sin intervención del factor tiempo, es realmente muy importante la evolución del sonido en el tiempo para distinguir unos de otros.

Con mayor precisión (en la que no podemos entrar en esta entrega) realmente el espectro no es estático, constante, para cada instrumento. Más bien hay una evolución del mismo, especialmente intensa en los primeros momentos de cada nota. Una cuerda pulsada ‘brilla’ al comienzo y luego se torna más opaca (desaparecen rápidamente con el tiempo sus armónicos altos, para los que la madera es poco eficiente a la hora de vibrar). Sin embargo un viento metal suele arrancar con un sonido opaco y ve crecer el brillo a lo largo del tiempo, porque a medida que crece el soplido en el tubo y el metal entra en movimiento, poco a poco es más capaz de llevar la energía que recibe hacia armónicos altos.

Lo que nos lleva a pensar en el tercer elemento esencial en la síntesis sustractiva: las envolventes, que nos permiten no sólo modificar la intensidad del sonido durante el desarrollo de las notas, sino que (aplicadas a las frecuencias de corte de los filtros) nos permiten modificar el espectro y reconstruir (o aproximar) el timbre característico de muchos instrumentos y en el que esa evolución es esencial.

Jugando a medias con la acústica y con los conceptos esenciales de la tradicional síntesis sustractiva, hemos podido establecer un modelo (que se aplica en muchos esquemas de síntesis) basado en concebir la señal de los sonidos musicales a través del binomio vibrador/resonador y su necesaria evolución a lo largo de desarrollo de la nota, que llevan en los primeros sintes analógicos sustractivos, al uso de una estructura dotada de oscilador / filtros y envolventes.

Vibrador <--> Oscilador

Resonador <--> Filtros

Desarrollo <--> Envolventes

Volveremos sobre este modelo de forma repetida a lo largo de esta serie.