Síntesis (31): De AM a FM, intro a la modulación en frecuencia

Los que me seguís bien lo sabéis. Soy un devoto de la FM y ansiaba que llegara el día de comenzar a contárosla. Iniciamos hoy un viaje que durará varias entregas.

El objetivo último es que seas capaz de entender cómo se crean sonidos en síntesis FM (frequency modulation, o modulación de frecuencia). Tal como veremos es fácil establecer reglas y conceptos que nos ayudan a entender el papel de cada uno de sus parámetros, y que te permitirán plantear el diseño o la modificación de sonidos FM desde conceptos musicales y sonoros, no matemáticos ni de ingeniería.

De entre las diferentes técnicas de síntesis, siempre he sido muy partidario del uso de la síntesis FM. Hay para ello varias razones, incluso ‘vitales’ como el que los DX apareciera cuando yo tenía 15 años, una edad en la que todo deja huella para siempre y en la que te apuntas a cualquier revolución (y los DX fueron sin duda una de gran calado). Pero principalmente mi interés se fundamenta en que ofrece unos timbres que contrastan y complementan muy bien los que obtenemos con otras estrategias. Tan cierto es que no podría vivir sólo con FM, como lo es que no podría vivir sin ella. No sería nunca el primer sinte que me llevaría a una isla desierta, pero sí el segundo, sin duda.

Los principios de la síntesis FM se pueden aplicar no sólo en los sintes Yamaha FM, como los clásicos DX, sino en otros muchos, ahora que la patente ya está agotada. A lo largo de estos capítulos usaremos varios sintes diferentes, incluyendo el excelente Dexed (plugin VST gratuito), el ambicioso FM8 (plug in de los de rascarse el bolsillo), la app FM4 para iOS (tremendamente sencilla de usar), o en cuanto a sintes hardware un Alesis Fusion y, cómo no, un FM de Yamaha, que no va a ser el DX7 sino el TG77.

En sistemas analógicos, como ya vimos con AM, es realmente difícil llegar a tener la precisión requerida para que la FM pueda resultar útil más allá de lo más básico (sonidos acampanados o pequeñas animaciones para dotar de movimiento a la señal de los osciladores), así que los dejaré fuera de las demos, pero lo que aprendáis podréis intentar llevarlo también a ese terreno. Especialmente con analógicos virtuales, o con analógicos dotados de DCOs (hay una FM útil por ejemplo en los Pro-2 y Prophet-12).

Hoy ofreceremos una presentación general, ubicaremos la FM en el contexto de otras técnicas de síntesis y marcaremos especialmente las diferencias con la AM. Va a ser una entrega ‘ladrillo’ que compensaré en las siguientes. Hoy toca poner los codos sobre la mesa.
He preferido ser un poco canalla y reservarme los primeros ejemplos audio para la entregas siguientes en las que revisaremos conceptos básicos a través un estudio (y escucha) más detallado del par modulador+portador; entraremos en conceptos avanzados tales como estructuras multioperador, modulación en paralelo y en cascada, o automodulación; y también recorreremos una panorámica del mercado comentando dispositivos hardware y software para FM.

Como siempre abierto a que preguntéis lo que no quede claro en cada capítulo, y dispuesto a intentar que la mayoría acabemos como usuarios expertos y capaces de desenvolvernos al crear sonidos en este otro tipo de síntesis.

El análisis de varias señales musicales que hacíamos en las primeras entregas nos permitía concebir muchos sonidos musicalmente útiles como la reunión de una colección de parciales cuasisenoidales generalmente relacionados entre sí de forma armónica, más una componete adicional de ruido (bajo la que podíamos incluir tanto ruidos ‘de fondo’ como los soplidos, o ruidos ‘impulsivos’ como la llave del clarinete o el golpe del martillo del piano, o la acción inicial de la púa en la guitarra).

Es en la parte de la recreación del conjunto de parciales / armónicos donde solemos poner más énfasis al hablar de síntesis. La síntesis aditiva se revelaba como un modelo casi inmediato, traduciendo cada parcial en forma de un oscialdor senoidal adecuadamente gobernado en nivel y frecuencia. Pero sumar uno a uno los parciales era un modelo costosísimo de implementar y costosísimo de manejar.

La síntesis sustractiva plantea la situación de otra forma, casi a la inversa: partamos de un sonido extremadamente rico en armónicos(dientes, pulsos, etc.) y mediante filtros retiremos lo que sobre. Adecuamos así el nivel de cada uno de los armónicos. Pero para ser suficientemente precisa esta síntesis necesitaría filtros muy flexibles que van más allá de los paso bajos y paso altos habituales. Se requerirían filtros ‘de formantes’ o capaces de impartir a la vez varias resonancias y gobernarlas. No suele ser el caso. Además en tecnología analógica la escasa variedad de las formas de onda (dientes, rectangulares, senos, triangulares, y poco más) no ayudaba a obtener una riqueza y variedad de colores como nos prometíamos los fanáticos de la creación de sonidos al empezar a estudiar el lenguaje de los sintes.

Con tecnología digital, las formas de onda de partida ya podían tener otros diseños. Los osciladores basados en look-up tables pudieron ofrecer variadas formas de onda ‘grabadas’ que correspondieran al tipo de distribución de armónicos presente en varios instrumentos. Salíamos así del estricto marco definido por las formas analógicas tradicionales y los filtros simples. Llegar de ahí a la idea de las wavetables como forma de variar el timbre ‘en la fuente’, ya en el oscilador, era un paso sencillo pero que abrió muchas posibilidades.

Me dejo por el camino muchas cosas (que ya veremos, como la síntesis granular o los modelos físicos, etc.) y me centro en lo básico: aditiva implica que combino varios parciales individuales para crear el sonido compuesto; sustractiva implica que parto de un sonido desproporcionadamente rico en armónicos para tamizarlo con filtros. Pero en uno y otro caso, al final el diseño del sonido se suele concebir (para analizar y para sintetizar) mejor a través del concepto de resonancias: de zonas, dentro de todo el espectro, donde el sonido presenta un realce, una mayor energía. El modelo excitador+resonador que comentábamos en su momento.

Las técnicas de AM que hemos tratado nos han permitido conseguir una capacidad curiosa e interesante para estos propósitos: la de ubicar un juego de armónicos allí donde nos interese. Una señal convencional, como un diente filtrado, contiene un juego corto (tanto como defina el filtro) de armónicos, concentrados en torno a frecuencias bajas. Las técnicas AM nos permiten llevar ese grupo de armónicos a ambos lados de una frecuencia portadora que podemos elegir. Con ello conseguimos crear la presencia de un grupo de armónicos allí donde los deseemos. Algo que podemos asimilar a crear una zona de resonancia. Pero para hacerlo necesitamos todavía contar con esa señal que ya es de por sí multiarmónico y que vamos a trasladar multiplicándola por un seno de la frecuencia central deseada.

Hoy veremos que FM permite la ‘magia’ de partiendo de dos senos crear extensísimas series de parciales. Series de parciales que podrán ser armónicas o no, al modo de lo que nos sucedía con AM, en función de si seleccionamos frecuencias relacionadas de forma entera o no. Series además en las que podremos controlar con facilidad la extensión del número de armónicos.

Se trata lógicamente de realizar modulaciones en las que la señal moduladora alterará, no la amplitud de la portadora, sino la frecuencia de dicha portadora. Mientras una modulación de la amplitud a velocidad lenta (por ejemplo con un LFO a menos de 10Hz) generaba un trémolo, la modulación de la frecuencia (aplicar ese LFO a la ‘afinación’ de un oscilador) genera vibrato. Y por ahí es por donde empezó todo.

… No se si fue el tercer o el séptimo día, pero dentro de la creación de las diferentes técnicas, el dios de la síntesis decidió crear la FM. Más que ningún dios (aunque muchos lo tengamos en nuestros altares particulares), en el caso de FM fue John Chowning. En sus investigaciones dentro del CCRMA de la Univ. de Standford para el que todavía trabaja, estudiaba siendo joven el vibrato. Llevando la velocidad del vibrato fuera de los rangos ordinarios encontró timbres atractivos y publicó en 1973 su artículo ‘The Synthesis of Complex Audio Spectra by Means of Frequency Modulation’ que representa un hito de su investigación. Unos resultados suficientemente maduros para el paso a la comercialización que realizó Yamaha en los años 80 adquiriendo los derechos para explotación de las ideas de Chowning e inundando a continuación el mercado con los exitosos sintetizadores DX.

Había ya usos anteriores de la FM en síntesis (como demuestran varios manuales de sintes analógicos), pero con un alcance mucho más limitado, centrado en efectos para generar parciales inarmónicos y campanas y percusiones de todo tipo. Chowning demostró la viabilidad de la FM para la obtención de sonidos ‘afinados’, y la aplicó para ofrecer aproximaciones sintéticas a los sonidos de un buen número de instrumentos acústicos que en aquella época resultaban atractivos y realistas.

El propio Chowning, junto a David Bristol, escribió el libro ‘FM Theory & Applications, by musicians for musicians’, editado por Yamaha en 1986 (ISBN 4-636-17482-8), aclarando los entresijos de la síntesis FM y ejemplificándola en tutoriales realizables sobre los DX. Un libro quizá tardío, pues llega ya en un cierto declive de la popularidad de la FM debido a la llegada de los sintes basados en sonidos muestreados (los romplers tipo Roland D50, o Korg M1), pero cuya lectura (si manejáis inglés y algo de matemáticas) es útil.

Demostrada su validez como técnica de síntesis en esa ‘recreación’ de instrumentos, luego fue aplicada con más espíritu innovador y creativo para la creación de un amplísimo catálogo de grabaciones. Se acusa por algunos, de forma totalmente injusta, a la confluencia de MIDI y la síntesis FM (que coincidieron en su comercialización a principios de los ochenta) de convertir en especie en extinción al ‘sintesista’, por haber traído la desaparición de los sonidos personales en pro de los bancos de ‘presets’. Es cierto que la desaparición de los controles (escasísimos en los sintes DX) y la aparición de las ‘memorias’ o ‘presets’ de sonidos (con capacidad para cientos de ellos en un único sintetizador), desmotivaron a muchos (en los terrenos del pop) a indagar en las posibilidades de creación de nuevos sonidos con FM, pero eso no desdice del potencial de la FM.

La FM está detrás de un buen número de grabaciones que son hitos de la música electroacústica y de vanguardia como varias de Barry Truax o las grabaciones del propio Chowning como Turenas, Stria, Phone, y otras. Hay una serie de años en que la actividad de compositores en el propio CCRMA, el IRCAM y casi todos los centros de investigación y composición es intensísima en torno a la FM.
Si nos centramos en música electrónica popular y de baile hay en los 80 infinidad de discos que usan sintes FM. Cualquiera que oiga el sonido ‘Lately Bass’ de un sinte DX puede enumerar a continuación evocar una larga lista de temas que lo usan, y no digamos ya la campana del DX7 o su sonido de armónica o el omnipresente piano ‘Tines’.

Pensemos primero (al estilo de lo que le sucedió a J. Chowning) en algo que todos conocemos bien: el vibrato, o si lo preferís llevar a nuestro terreno, la aplicación de un LFO al ‘pitch’ en un sinte. Pensemos en una nota, por ejemplo un La 440Hz. La frecuencia del vibrato (de la modificación del tono) es a lo sumo de unos pocos Hz. y por tanto muy inferior a la frecuencia del propio tono que se ve modificado. También es importante considerar la intensidad del vibrato, que tiene que ver con la extensión del desplazamiento arriba/abajo sobre el valor original de 440. Un vibrato ligero puede estar subiendo unos pocos Hz, uno más intenso puede llegar incluso a ser de semitono o más (sucede en cantantes y en los momentos más arrebatados de un violinista).

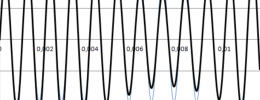
En todo caso, se trata de que la afinación (la posición de la raya en el espectro) no cesa de moverse, y con ello lo que debería ser una raya estilizada y fina se convierte en una raya borrosa y engrosada. La veis aquí.

Para que lo podamos ver mejor tendríamos que usar una lupa y descubriríamos que realmente existe estructura, no es un simple ‘engrosamiento’ borroso. Voy a mostraros un ejemplo en el que una senoide de 2000 Hz es sometida a un vibrato de unas pocas decenas de Hz, pero sería el equivalente en esa frecuencia alta a lo que antes os mostraba en 440. De esa forma podremos ver la estructura interna, sin necesidad de lupa ni microscopio.

Podéis apreciar la existencia de un grupo de rayas equiespaciadas, es decir no es caos, hay estructura. En torno a la frecuencia portadora (esos 2000Hz centrales y destacados) aparecen rayas por encima y por debajo a distancias múltiplo de la velocidad del vibrato. Bienvenidos a la FM.

Una vez que apreciamos el hecho de una estructura de rayas equiespaciadas, el aprovechamiento para crear sonidos armónicos está al alcance. El LFO no es más que un segundo oscilador limitado a velocidades ‘lentas’ de variación. Pensemos (como ya hicimos en AM) que en lugar de un LFO usamos dos osciladores idénticos, uno portador y otro modulador pero ambos capaces de trabajar en frecuencias audio, y adentrémonos así en la FM.

El número de parciales

Tal como nos sucedía en AM, la frecuencia portadora nos permite ubicar ese resultado FM (ese grupo de rayas) en torno a una frecuencia, la que nos interese. Y la frecuencia de la moduladora va a determinar la apertura entre las rayas. Cuando seamos capaces de sintonizar las dos frecuencias (portadora y moduladora, fp y fm) a una relación entera sencilla, el resultado será armónico.

Pero fijaos bien en las diferencias: en AM concebíamos el resultado como un ‘traslado’ del espectro de la moduladora para recentrarse en torno a la portadora. Si la moduladora era una senoide, daba lugar a una única raya lateral a cada lado de la portadora. Cuando subía o bajaba el índice de la modulación lo que conseguía era subir o bajar el nivel de ese par de rayas lateral respecto a la raya de la portador. Pero un espectro ‘cortito’ como el del seno portador, seguía siendo ‘cortito’ en su nueva ubicación alrededor de la portadora.

En FM estamos viendo que aparece, incluso con una moduladora senoidal, todo un conjunto de rayas, un agrupamiento, una familia. Son varios los pares de rayas laterales que genera. FM se revela así como una modulación ‘explosiva’ en el número de rayas que genera. En seguida es capaz de generar espectros llenos de parciales, incluso partiendo de la aparente debilidad de dos senoides. Si en AM hablábamos de ‘trasladar’ el espectro, aquí lo que tenemos es el poder de generar conjuntos de parciales con la intervención de dos meros senos. Nada que ver.

La anchura y forma espectral

Otro aspecto importante tiene que ver con cómo se modifica el espectro FM al variar el índice de modulación, es decir cuando dejamos que la moduladora desplace con mayor o menor recorrido la frecuencia inicial de la portadora.

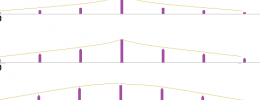
Aquí tenéis el resultado a través de varias imágenes:

Veis como lo que sucede es que el índice de modulación (en última instancia la amplitud con la que la moduladora actúa sobre la frecuencia portadora) puede servir como elemento de control de la apertura o cierre del conjunto de rayas. Es decir, realiza un control de timbre, de anchura espectral. En cierta medida, al modo de un filtro paso banda, para que lo asimiléis a algo conocido.

Al subir la amplitud de la moduladora, la excursión que realiza la frecuencia de la portadora crece y eso genera un espectro más ancho, pero que, graciosamente, no pierde la estructura de rayas equiespaciadas. Un resultado muy musical, muy útil conceptualmente para entender la actuación de la FM, porque nos permite asociar a la amplitud de la moduladora el resultado tímbrico de crecer/disminuir el ancho de banda.

Si siguiéramos subiendo ese índice, dejamos de obtener ese comportamiento regular que observamos en esas primeras figuras, caracterizadas por que los armónicos centrales eran los más fuertes y luego había una caída progresiva de nivel hacia los laterales. Se mantiene el juego de rayas equiespaciadas, se mantiene el que el espectro va ocupando un mayor ancho de banda, pero llega un momento en que el reparto de la energía entre las rayas ya no es monótonamente decreciente hacia los lados.

Si siguiera subiendo la amplitud de la portadora, veríais cosas como estas:

Fijaos cómo las rayas centrales (antes las más preeminentes) pierden primero fuerza respecto a otras, y luego se van produciendo otras diversas distribuciones con picos y valles en la zona central. En todas ellas los extremos de la banda ocupada sí son ‘decrecientes’ pero la actividad en la zona central tiene un comportamiento muy dinámico, con mucho movimiento, con mucha cesión de energía entre unos armónicos y otros. Con ‘huecos’ que se abren sobre una zona central en la que se concentran los armónicos más fuertes. Recordad que es una escala en dB, así que las diferencias de nivel son realmente fuertes, y en particular los armónicos finales de cada lado están muy rebajados ya.

Lo apreciáis aún más en estos otros casos, tomados (como los anteriores) de Dexed, un simulador de DX7 en VST gratuito. Estas tres últimas figuras corresponden ya a los valores máximos de intensidad con la que el modulador puede actuar sobre la portadora dentro del DX7 (no está nada mal con sólo 2 senos acabar generando unos 40).

Otra cuestión más quiero destacar como una propiedad de la FM merecedora de su propio apartado. Fijaos en qué pasa cuando modulo la frecuencia de un tono mediante otro:

Hay una cuestión importante: la señal modulada en frecuencia no ve modificada su amplitud por el hecho de la modulación. Varía su frecuencia, sí, pero su nivel, su intensidad, es la misma que antes de la modulación. No es una observación irrelevante. Cuando filtramos en un sustractivo como forma de variar el timbre, estamos afectando al nivel (baja porque retiramos algunas componentes), cuando hacemos síntesis aditiva cambia el nivel (la suma de los senos y sus proporciones afecta al nivel final), cuando realizamos AM por definición se afecta la amplitud del resultado. Pero en FM no, en FM podemos controlar con estricta independencia nivel y timbre.

Es independencia absoluta entre timbre e intensidad se da en la FM y eso no sucede en otros muchísimos tipos de síntesis. Cuando usáis una envolvente para un filtro, estáis simultáneamente realizando un cambio de intesidad, a veces sin querer. En FM cada cosa se gobierna de una forma.

Una envolvente de amplitud aplicada a la moduladora, estará afectando abriendo y cerrando el espectro, tal como veíamos antes, pero sin modificar la amplitud final de la señal, sin añadir ni quitar energía, manteniendo su intesidad.

Una envolvente de amplitud aplicada a la portadora, estará afectando subiendo y bajando el volumen, pero no realiza ninguna actuación sobre el contenido espectral.

Este es un aspecto también muy interesante en FM. Mientras en sustractiva arrancar un sonido con un filtro cerrado y luego abrirlo conlleva que el sonido inicial es débil y el final fuerte (salvo que intentemos compensar con una envolvente diferente de amplitud) en FM podemos controlar cada cosa por separado. Y esa independencia es control en tus manos, y al final también simplicidad. Tocar una envolvente de un filtro en un sustractivo te lleva a necesitar retocar la envolvente del VCA. Aquí en FM, no. Usa una rueda para la frecuencia de corte en un sustractivo y cuando cierres el filtro tu sonido se ahogará. En FM puedes abrir y cerrar el espectro, sin perder sonoridad.

Si quisiérais determinarlo con exactitud, el espectro de una señal modulada en FM no es fácil de calcular, exige unas matemáticas avanzadas en las que no pienso entrar aquí. Pero podemos observar lo que sucede e inferir una expresión práctica de lo que las matemáticas cuentan con mayor rigor.

Os resumo las figuras anteriores en esta nueva:

Observamos (y las matemáticas pueden demostrar) que si partimos de considerar un seno de frecuencia fm modulando a otro de frecuencia fp, el resultado es un conjunto de componentes de frecuencias fp -/+ k fm (con k tomando valores 0, 1, 2, 3…), cuya distribución de amplitudes varía en función de la intensidad de la modulación.

Para intensidades pequeñas (es decir, cuando el nivel de la moduladora es bajo, y por tanto la excursión de frecuencia que causa es de pequeño recorrido), se trata de un grupo de parciales no muy abierto, y además concentrado en forma de montaña, con las rayas centrales más fuertes y progresivamente las otras más reducidas. Para intensidades más grandes no se mantiene esa idea de montaña, sino que va habiendo una variación mucho más compleja.

En ese resultado complejo, los extremos últimos (media docena de rayas finales a cada lado) sí son decrecientes, pero en la parte ‘interior’ hay un nivel ‘promedio’ que se mantiene, pero con unas fuertes diferencias de nivel entre unos y otros parciales (en esos ejemplos veis en la zona central excursiones que alcanzan los 12 y 18 dB). Y toda esa variedad bajo el control de un único parámetro: el nivel de la moduladora, su amplitud (y a través de ella el control de la profundidad de la modulación que genera ese espectro cada vez más y más abierto).

De hecho las amplitudes de los sucesivos parciales están descritas por las funciones de Bessel de 1ª especie y orden k, en función de la intensidad de la modulación, y aunque había prometido no pasarme del lado matemático, es demasiado bonito como para que no lo veais:

• Vivan la FM y el John Chowning que la parió
• FM nos permite separar completamente el control del timbre y el de la intensidad
• La frecuencia de la portadora es en la que se ‘centrará’ el espectro resultante
• Aparecen múltiples rayas laterales a ambos lados de fp
• Esas rayas están a distancias múltiplo de fm y están por tanto equiespaciadas fp+/- k*fm
• Si aprovechamos relaciones enteras entre fm y fp podemos hacer coincidir las rayas con una serie armónica y tener sonidos ‘afinados’ (aquello de los 'puntos dulces' que mencionamos al hablar de AM)
• La profundidad con la que la moduladora desplace la frecuencia portadora da lugar a que el espectro resultante esté más concentrado o más abierto, casi funcionando como un control de ancho de banda generado en torno a la portadora a partir de la amplitud de la moduladora
  • Si la moduladora es de pequeña amplitud, mucha energía sigue en la frecuencia central el resto aparece en esas otras rayas laterales con cada vez menor nivel (la distribución ‘global’ tiene forma de montículo), con lo que se parece a un filtro
  • Si la moduladora crece, se pierde mucha energía en la raya fp que va destinada a incrementar las otras rayas laterales, y además esas rayas laterales dejan de estar concentradas en forma de montículo y empiezan a adoptar configuraciones más ‘estrambóticas’

Ya para rematar, cedo la palabra al propio J. Chowning en un vídeo del AES en el que relata los orígenes de la FM.