Tecnología en retardos: de A a D pasando por BBD (2/2)

En la primera parte (https://www.hispasonic.com/tutoriales/tecnologia-retardos-a-d-pasando-bbd-1-2/38414) presentábamos tecnologías no digitales para retardo (incluidos los BBD), así que hoy toca acudir a los bits y profundizar en las comparaciones de unas y otras soluciones.

La idea de la cadena de cubos de agua que servía como descripción de los BBD es también extrapolable a una de las posibles (y primeras) implementaciones para el diseño de retardos digitales. Aunque está claro que aquí los bomberos no pierden ni una gota de agua por el camino: se trata de circular un valor numérico por una memoria y en la circulación de ese valor por hardware o software digital no hay ruido añadido, el número no se ‘deforma’ ni ‘ensucia’. Como resultado muchas de las deficiencias de los sistemas BBD y analógicos no están aquí (salvo que las reintroduzcamos con inteligencia para evitar un resultado ‘demasiado perfecto’), lo cual no quita que se presenten problemas propios.

Como sabemos un A/D permite obtener una representación de tiempo discreto (sólo en instantes concretos, definidos por la frecuencia de muestreo) mediante una ristra de bits (en esencia un ‘número’ que habla de la amplitud de la señal en ese instante). A la inversa un D/A recupera la señal original a partir de sus muestras (esos números que se suceden).

Si entre medias situamos un conjunto de registros que a golpe de un reloj vayan pasándose el valor que cada uno contiene, tenemos una traslación literal del concepto ‘retardo BBD’ al mundo digital (en realidad históricamente es al revés: como ya existía el concepto de retardo digital pero era caro, se concibió el mecanismo BBD para hacerlo viable, portable y a costes razonables).

Una batería de registros enganchados de esta forma, en ‘cascada’, no es sino una memoria FIFO (first in, first out). Algunos de los primeros retardos digitales se basaban estrictamente en esta idea de ‘cascada’ de registros (lo del cubo de agua). Incluso en ellos para conseguir tiempos de retardo ajustables lo que se hacía era variar la velocidad del ‘reloj’, es decir acelerar o decelerar el muestreo (con lo que una cadena de un número fijo de elementos sería recorrida en menor o mayor tiempo).

Pensadlo un momento. ¿No estamos variando la frecuencia de muestreo (tanto aquí como en los BBDs)? Sí, por supuesto. Y eso conlleva que o bien los filtros antialias y de reconstrucción los hacemos también variables o bien que hay que diseñarlos para el caso peor: ajustando su ancho de banda para que se evite el aliasing en la velocidad más lenta. Pensad que un BBD típico (o en los primeros modelos digitales), la frecuencia del reloj podía variar por ejemplo entre 10KHz y 100KHz. Eso significaría que el ancho de banda puede ser tan corto como 5KHz o tan generoso como 50KHz. Y limitar a 5KHz es mucho limitar…

Tanto en los diseños BBD como en los digitales basados en esta arquitectura que acabamos de presentar encontraréis modelos ‘caros’ que usan filtros de corte variable (y que se ajusta simultáneamente al propio tiempo de retardo) o diseños ‘baratos’ con filtros fijos.

En el primer caso (los ‘de alta gama’) existe un efecto curioso (y que es parte del carácter de esos sistemas): cuando ajusto tiempos cortos de retardo, los ecos ‘brillan’ más, tienen mayor ancho de banda. En el caso de los segundos (los de filtro fijo) habrá un sonido permanentemente ‘opaco’ (filtrado) o bien (si no está ajustado al caso peor, sino a un ancho de banda algo más alto) cuando ajuste valores largos de retardo comenzará a aparecer una dosis apreciable de aliasing.

El ejemplo es interesante porque nos muestra cómo determinadas tecnologías y formas de diseño, pueden acabar generando resultados bien diferentes sobre algo que concebíamos como igual. ¿No se trataba sólo de tener un ‘retardo’, una ‘copia retrasada’ de la señal de origen? Tal como estamos viendo, cada forma de diseño conlleva sus propios pros/contras, su propia ‘huella’.

¿Y entonces en qué mejora este diseño digital al clásico BBD? Las ventajas de lo ‘digital’ frente a lo ‘analógico’ se manifiestan aquí por ejemplo en que si queremos aumentar la duración del tiempo de retardo (haciéndola incluso de segundos) basta aumentar suficientemente el número de registros. Pensad en los BBD. Incluso uno de 4096 etapas, a una velocidad de muestreo de 40000Hz sólo permitiría un retardo máximo de una décima de segundo. Y usando BBDs no vale concatenar muchas unidades de 4096 etapas (o fabricar integrados con más etapas) porque la cantidad de ruido y otros problemas (distorsión, etc.) sería ya demasiado grande. De hecho, en algunas simulaciones digitales de sistemas antiguos de retardo es necesario introducir ruido, para obtener un resultado más fiel (aunque sea mermando la ‘calidad’).

Está claro pues, que salvo con sistemas de cinta, antes de la llegada de las soluciones digitales, un sistema ‘de escenario’ para retardo no podía pretender ir mucho más allá de retardos cortos (salvo con severas limitaciones de ancho de banda: para medio segundo de retraso un BBD de 4096 etapas debería funcionar a velocidad de muestreo de aprox. 10KHz y tendría limitado a 5KHz su ancho de banda útil sin aliasing).

Esta v1 de retardo digital queda pues como una réplica (aunque con alguna mejora) de los BBD, y hereda buena parte de sus problemas. Especialmente la cuestión del alising/filtrado, si bien el ruido estará más bajo control y ello permitirá alcanzar retardos de mayor duración. Respecto a la necesidad o no de incluir compresión y expansión (algo habitual en los diseños BBD) aquí estaríamos sujetos al margen dinámico de los conversores A/D y D/A. Hoy en día (con 16 o 24 bits) posiblemente no usaríamos compresión y expansión, pero si pensáis que entre los primeros diseños comerciales digitales los hay con conversores de 8 bits y 12 bits, en esos casos sí es fácil que se esté usando compresión/expansión (o bien conversores no lineales que implican también una cierta compansión).

Esas no linealidades añaden su carácter, de la misma forma que lo añadía el grabar en cinta magnetofónica o el pasar por un circuito de válvulas. Y esas no linealidades normalmente no estarán presentes en un diseño digital de un puro retardo a día de hoy. Por ello veréis últimamente que en algunas unidades de efecto se incluyen algoritmos llamados ‘vintage delay’, ‘analog delay’, ‘tape delay’ (o semejantes), en ellos podemos esperar que algunas de las características de las tecnologías antiguas (ancho de banda limitado, ruido interno, distorsión, vinculación entre tiempo de retardo y brillo…) sean imitados (más tarde vemos alguno).

La v1 era coincidente en su esencia con la idea que subyacía en los BBDs. Pero la mayor parte de los retardos digitales a día de hoy están resueltos de otra forma (y que como veremos, da lugar a otras características en su respuesta). En lugar de una batería de registros por los que circulan las muestras (lo que implica que continuamente están circulando valores por todo el circuito, cada pulso de reloj todos los registros cambian de valor), el A/D va cargando (en forma ‘circular’: cuando llega al final vuelve a comenzar por el principio) una memoria. De forma parecida el D/A va leyendo esa memoria (también en forma circular) pero siempre leyendo valores ‘antiguos’ (leyendo ‘por detrás’ de donde se va escribiendo en la memoria). En definitiva, en lugar de circular los valores por toda una cadena de registros, empleamos una memoria y una gestión de ‘punteros’ de lectura y escritura. Vamos escribiendo (y leyendo) sobre direcciones sucesivas de esa memoria.

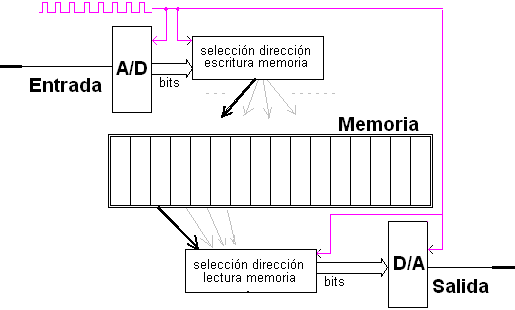
Pensemos cómo se resuelve en esta arquitectura el ajuste del tiempo de retardo (que antes nos obligaba a variar la frecuencia de reloj). Una posibilidad (de nuevo) sería variar la frecuencia de reloj, pero ahora hay otra alternativa: es suficiente modificar la selección de la dirección de lectura (la distancia entre dónde escribimos y dónde leemos, de forma semejante a lo que hacían los 'ecoplex' de cinta con su posibilidad de desplazar las cabezas). Si va ‘muy’ por detrás de la de escritura tenemos retardo largo, si va sólo ‘ligeramente’ por detrás tenemos retardo corto.

Con esta estrategia no hemos necesitado cambiar la velocidad del reloj. Los conversores A/D y D/A, así como todo el resto del sistema, funcionan siempre a velocidad de reloj fija. Por ejemplo a 32KHz, o 44,1KHz o a 48KHz (según la calidad que deseemos). Garantizando así (ya sea con retardos cortos o largos) que el ancho de banda permanezca idéntico todo el tiempo (y pudiendo controlar el aliasing mediante unos sencillos filtros fijos). Es decir, permitimos ahora el ajuste del tiempo de retardo sin los problemas que ofrecía la arquitectura de ‘brigada de bomberos’ o su equivalente digital más directo respecto al corte de los filtros antialias y de reconstrucción.

¿Magnífico? Ni sí ni no. Sólo distinto. Porque esta estrategia tiene (cómo no) sus contrapartidas. La más evidente es la que describo ahora (y que nos obligará a definir un retardo digital v3).

¿Qué retardo queréis ajustar? Por ejemplo ¿9 o 10 ms? Siempre hay alguien que responderá 9,65723 ms. (y tal vez no siempre sea por ganas de incordiar, sino por alguna causa legítima). En los BBD y en lo que he denominado ‘digital v1’ podíamos variar la velocidad del reloj de muestreo para conseguir cualquier duración deseada. Pero ahora, en la v2, las variaciones son ‘por saltos’, no por el ajuste continuo de la velocidad del reloj. Puedo tener un retardo de 9000 o 9001 muestras, pero no de 9000 y media. Y lo que es más grave: puedo tener un retardo de 5 o 6 muestras, pero no de 5 y media.

Si la variación del tiempo de retardo la queremos sólo para ajustar aproximadamente ‘a tempo’ un eco (es decir, queremos poder variar el tiempo de retardo, pero en el uso, una vez ajustado el valor, no vamos a modificar ese tiempo) esta arquitectura ‘digital v2’ parece funcionar bien. Además en un uso de tipo ‘eco’ el tiempo de retardo es relativamente grande, y por tanto no importa mucho el que en lugar de ‘9000 y media’ lo dejemos en 9000 o en 9001. En el caso de muestreo a 44,1KHz esas 9000 muestras corresponden a 204,08 ms. y las 9001 muestras a 204,10, con lo que el error o diferencia es del 0,01%, inapreciable.

Pero pensad en el caso de tiempos de retardo cortos (como en el ajuste de un filtro peine, que deseo sintonizar a cierta frecuencia) o en el caso de que el tiempo de retardo ‘se mueve’ (como en un flanger). De nuevo pensando como ejemplo en que la frecuencia de muestreo sea 44,1KHz, un filtro peine a partir de la solución ‘digital v2’ ajustado a 10 muestras tiene el peine sintonizado a 4410Hz, mientras que con 11 muestras resuena sería a 4009: un salto en frecuencia de un 10% (que es ya de unos cuantos semitonos, un salto claramente apreciable). Suponed que en vez del filtro peine se trataba de un flanger (con tiempos que están variando continuamente). La variación va a ser ‘a saltos’, en escalera (de forma parecida a como en algunas malas emulaciones digitales de sintes analógicos un barrido del filtro se oye ‘escalonado’).

¿Imposible por tanto el clásico flanger que realiza barrido suave en una realización digital? ¿Imposible sintonizar un peine a voluntad? No, pero claramente esta solución ‘digital v2’ no nos vale. Tenemos que inventar otra o refinarla.

Por cierto, la mayor parte de los retardos que he visto en las workstations y módulos de síntesis tienen este problema (incluso en algunos equipos dedicados a efectos). El ajuste del tiempo de retardo se realiza (como mucho) llegando a la resolución de una muestra, y eso los hace inviables para algunos usos. También con plug-ins podéis encontraros varios que son inhábiles para generar retardos ‘con decimales’ (de 0,5 muestras por ejemplo) o si preferís llamarlos así retardos ‘fraccionarios’ (de 1/2 muestra, por ejemplo).

Si queréis experimentar en profundidad con filtros peine, lo siento, pero la mayor parte de las unidades de efecos en sintes y workstations no van a ser capaces de salvaros (salvo que tengan algún algoritmo específicamente concebido para ello y que permita ajustar retardos fraccionarios). Si queréis usar un delay controlando el tiempo de retardo mediante comandos de control para realizar un ‘flanger manual’ (en vez de disparado desde un LFO) nuevamente este tipo de solución v2 va a ser muy poco recomendable.

Demos pues un paso más.

Si me limito a ofrecer hacia el D/A los propios valores que el A/D ha ido cargando en la memoria, tengo ese problema de no poder realizar retardos ‘fraccionarios’ (de 6,5 muestras –seis muestras y media- o de 6,1 muestras) sencillamente porque esos instantes no están ahí, no han sido capturados. ¿Han sido perdidos para siempre? ¿Es imposible reconstuirlos? ¿Final de la historia? Bien sabemos que no. Todos tenemos o hemos usado flangers digitales (como tantísimos incluidos en sintes o unidades de efecto digital) que no tienen el efecto ‘escalera’.

Algo están haciendo esos flangers para ‘adivinar’ el valor que caía entre dos muestras (recordad que un flanger –también un chorus- tiene retardo variable y que por tanto sólo casualmente coincidirá con un número entero de muestras: la mayor parte del tiempo necesita conocer valores que había ‘en medio’).

Planteemos el problema sobre el caso de un retardo fijo y corto (el filtro peine que mencionábamos antes) y la posibilidad de obtener un retardo que caiga ‘entre dos muestras’. Pintemos la señal original y las muestras que el A/D obtiene de ella, así como los valores (no disponibles como muestras directamente en la memoria) que necesitaría recibir el D/A para poder escupir la señal con retardo de 1/2 muestra y de 1/10 de muestra.

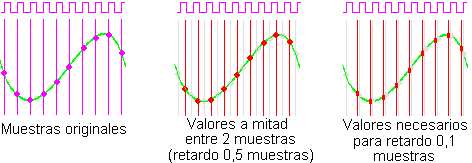
El ‘truco’ para obtener retardos fraccionarios y variables en los sistemas digitales es usar algún tipo de interpolación. Aquí tenéis a modo de ‘zoom’ lo que pasa en el espacio entre dos muestras (de nuevo vemos las muestras originales y los valores de los que desearíamos disponer para ‘conocer’ la señal que había con retardo media muestra y un décimo de muestra).

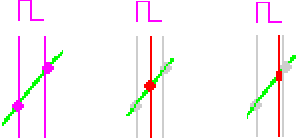
Como la velocidad de variación de la señal está limitada (cualquier señal digitalizada habrá sido sometida a filtrado antialias, acorde al teorema de Nyquist), el recorrido entre dos muestras es relativamente ‘suave’, y el valor de la señal puede ser reconstruido partiendo de las muestras disponibles.

En la figura anterior, parecería incluso que una interpolación ‘lineal’ (uniendo las dos muestras disponibles con una línea recta y aproximando el valor en cualquier punto intermedio entre ambas muestras por el valor de la recta en dicho punto) sería suficiente, no estaría muy lejos del real (no añadiría demasiado ‘error’ o ‘ruido’). Eso corresponde a un cálculo muy simple, fácil de realizar en un sistema digital (dos multiplicaciones y una suma).

En realidad no es tan simple si queremos tener una buena calidad, y es necesario contar con la información de más muestras próximas para poder reconstruir correctamente. Puede ser mejor (más precisa) una interpolación parabólica (en vez de lineal), y mejor aún si intervienen en lugar de 2 o 3 muestras, un número mayor de ellas. Sólo con esas interpolaciones de mayor orden se llega a poder reconstruir la ‘curvatura’ exacta que seguía la señal original en el espacio que media entre dos muestras.

Os dejo en un anexo (al final del artículo) una mención al interpolador ideal y su uso en el caso digital (es ya demasiado técnico / matemático, pero algunos habéis preguntado al respecto).

Los flanger y chorus digitales (que necesitan retardos variables, y por tanto casi siempre fraccionarios) lo que hacen es interpolar, para obtener el valor que ‘desarían’ conocer de la señal de origen. Lamentablemente, muchos de ellos usan una interpolación muy básica (haciendo intervenir sólo a las dos muestras más próximas) con lo que sufren de un ruido/distorsión apreciable (que se incrementa en el flanger cuando usamos realimentación). Os sorprendería la cantidad (alta) de puntos que serían necesarios para conseguir mantener una calidad de audio de tipo CD (con un ruido generado suficientemente bajo). Ciertamente cualquier chorus o flanger digital es mucho más ‘limpio’ que los correspondientes en tecnología BBD / analógica, pero aún así se nota asociado a estos efectos un nivel crecido de ruido que sólo una interpolación más cuidada lograría reducir

Son estos detalles que diferencian (y mucho) los resultados (y coste) de un producto de alta gama respecto a uno ‘corriente’. En los sintes y workstations estamos presionando mucho a los fabricantes. Queremos el ‘todo en uno’ y exigimos un sinte potente, un secuenciador digno, varias unidades de efecto simultáneas… y, claro, a un precio reducido. Como contrapartida a tanta exigencia acabamos en muchas ocasiones teniendo, sí, todo eso que pedimos, pero con una calidad limitada. Para poder ofrecerlo sin tener que incorporar procesadores de mayor capacidad de cómputo –más caros-, el fabricante reparte la capacidad de cómputo del procesador o procesadores. Y generalmente a los efectos no se les va a entregar un porcentaje elevado. Los ‘delays’ generalmente sólo van a permitir ajustes del tiempo de retardo que sean de un número entero de muestras, la interpolación en los flanger y chorus va a ser muy pobre (lineal o incluso tomar la muestra más cercana; lo que sólo funciona bien para frecuencias bajas y medias-bajas, pero no para sonidos con alto contenido a partir de medias-altas), el ‘lfo’ del flanger y chorus va a seguir una ley triangular (en lugar de la más suave y preferible senoidal), las reverbs tendrán colas en las que se aprecian regularidades en los rebotes, y así podríamos seguir. Nos sorprende que las unidades dedicadas (y ‘caras’) disponibles en los estudios tengan un extra muy notable de calidad que no llegamos a encontrar en los efectos integrados, pero hemos de comprenderlo.

Cómodo como resulta usar el efecto ‘interno’, puede ser necesario desactivarlo y usar un ‘externo’ de alta gama si buscamos el máximo de calidad.

Pero no siempre buscamos el máximo de calidad (entendida como calidad 'objetiva'). Más que ‘Regreso al futuro’ (el título de una película), parece que en los sistemas audio tenemos a veces cierta tendencia a ‘Avanzar hacia el pasado’. Me refiero a la cuestión ‘vintage’, que cómo no, llega también a los retardos. Ya mencionamos en la primera parte que intentar reconstruir en hardware hoy un diseño basado en BBDs (y qué decir en cinta magnetofónica) resulta harto difícil. Los integrados BBD ya no se comercializan ni producen de forma masiva como antaño.

Las soluciones digitales nos permiten simular estos sistemas con tanta fidelidad como sea capaz de concebir quien diseña el software. Así que vayan unos ejemplos y reflexiones sobre la reconstrucción de unidades de retardo ‘clásicas’ de la mano de plug-ins en software. Tal como mencionábamos en la primera parte, obtener una simulación detallada de las peculiaridades de estos diseños clásicos (cargados de ‘defectos’ que imprimen una ‘huella’ propia, un color que imprime una ‘magia’ especial al sonido que los atraviesa) no es sencillo. Eso que definimos como ‘retardo’ y que aparenta ser una mera copia de lo que sucedió hace unos milisegundos, se acompaña en la realidad de ruido, distorsión y otras ‘gracias’ varias.

Para un profesional cuyo tiempo es oro y que, contratado por su valía como técnico, busca ofrecer un determinado resultado en un tiempo corto, si un determinado dispositivo ofrece ‘magia’ se adquiere y se usa. No hay necesidad de romperse la cabeza intentando recrearlo, pensando y probando diferentes soluciones hasta dar con una receta provechosa. Si el libro de recetas ya existe, basta seguirlas. La moda ‘vintage’ es para mi algo de este tipo: poder disponer de recetas muy socorridas y probadas, para resolver las necesidades de una mayoría de situaciones (siendo realistas, muy pocos proyectos son profundamente ‘creativos’ e ‘innovadores’).

Posiblemente podemos montarnos una cadena de plugins y ajustarlos hasta obtener un resultado igualmente agradable, y quizá podamos incluso al hacerlo mejorar algunos aspectos en los que esas unidades clásicas flaquean, pero nos llevará un tiempo importante de prueba y error, de diseño, de gasto en ‘creatividad’. Algo por lo que normalmente no nos pagan (aunque es desde luego una bendición cuando cae en tus manos un proyecto abierto a ese lado creativo y que busca huir de la ‘recreación’ y encontrar la ‘innovación’).

Hay que distinguir la labor (o los ratos) en los que trabajamos en modo ‘ingeniero de desarrollo’ pariendo ideas, y las labores (o ratos) en los que trabajamos en modo ‘técnico’ usando las ideas y productos que otros han desarrollado.

Como mera ilustración aquí tenéis un resumen de los plug-ins para retardo que ofrece Universal Audio (uno de los fabricantes de plug ins que de forma intensa desarrolla simulaciones de unidades clásicas). Con precios que se mueven entre los 100 y los 200 euros aproximadamente, veis en su catálogo reconstrucciones digitales de unidades de cinta, tanto de la familia EchoPlex (el EP-34) como de la familia Roland (RE-201), o de dispositivos basados en BBD (como el Dimension D). Pagar más de 100 euros por un Dimension D que no deja de ser un chorus que sólo tiene 4 ajustes fijos (sin posibilidad de ajustar ‘rate’, ‘depth’, etc; sólo modo 1, 2, 3, 4, o sea, cuatro ‘resets’) puede parecer a priori extraño, pero estamos pagando la reconstrucción simulada (y con un alto grado de detalle) de un sistema ‘mágico’ basado en BBD. Estamos comprando su magia.

Y por cierto, dado que habíais preguntado especialmente por el space-D de Roland, en la propia página de Universal Audio encontráis alguna información al respecto (han recreado en plug-in el Dimension D original: http://www.uaudio.com/store/delay-modulation/roland-dimensiond.html). El Dimension D (el rack con 4 botones) fue exitoso, porque conseguía un tipo de chorus especialmente suave, dulce y rico, frente a los habituales (en los que el efecto está demasiado expuesto: se nota la modulación y su carácter repetitivo). Como subproductos o evolución de ello, surgieron pedales como el Boss DC2 (que heredaba el nombre de Dimension D -todavía basado en BBD-) o su evolución el DC3 (ya en tecnología digital y por ello llamado inicialmente Digital Dimension, nombre cambiado posteriormente a Space D). A día de hoy muchos productos de Roland aprovechan el ‘marchamo’ de calidad que arrastra la denominación ‘Dimension’ o ‘Space D’ y aunque se trata de soluciones, arquitecturas y algoritmos bien diferentes, podéis encontrar en muchos sintes y workstations Roland un efecto ‘Space D’ (y que no hemos de confundir con los 3D Chorus y semejantes que también ofrecen y que combinan elementos de chorus con elementos de la tecnología RSS desarrollada por Roland para generar sensación 3D en audio).

Hablar por tanto de cómo está realizado el ‘Space D’ resulta difícil, puesto que hay múltiples sistemas diferentes que ostentan ese nombre. Es muy habitual este ‘aprovechamiento’ de las denominaciones exitosas para bautizar sistemas que no siempre son todo lo parecidos que uno podría suponer. Si nos vamos al original (el ‘Dimension D’) tenemos alguna pista sobre su funcionamiento en http://www.uaudio.com/blog/roland-choruses-under-the-hood. Dado que está en inglés, os resumo muy brevemente lo esencial.

Se trata de un chorus multivoz. Varios BBD independientes (cada uno con sus propios LFOs) se combinan para generar varias voces. Los cuatro botones determinan otros tantos ajustes ‘preset’ de los LFO, los retardos, y los niveles de mezcla de las distintas voces. Hasta ahí nada demasiado llamativo, la verdad. Pero la gracia, cómo no, hay que buscarla en que el Dimension D usaba compresión/expansión en los BBD (y por tanto introducía un cierto grado de ligera distorsión, que resulta ser agradable), usaba velocidad variable en los BBD para ajustar el tiempo (con lo que el ancho de banda de cada voz varía simultáneamente al propio tiempo de retardo), etc.

Intentar recrear esa ‘riqueza’ a partir de un chorus digital simple no es nada fácil. La magia, la receta, exige muchos más elementos y matices, y la labor de ‘ingeniería inversa’ para recrearlos en software tiene su precio.

Espero que os haya resultado interesante este recorrido desde la A a la D pasando por los BBD, y que nos ha llevado a mirar las tripas de nuestros efectos de retardo, interesándonos por su funcionamiento y diseño. Algo de luz espero que dé también sobre los resultados que obtenemos de ellos.

Conocer (y por eso este artículo en dos entregas) la parte de ingeniería y diseño nos viene bien por la cultura profunda que nos da para abordar la tarea como técnicos/usuarios. Entender el funcionamiento de nuestros efectos nos ayuda a comprender cómo suenan y a reconocer sus límites. Nos habilita mejor para detectar los límites de lo que podemos ofrecer con los sistemas de los que cada uno disponemos, y para saber valorar los esfuerzos que podemos llegar a desarrollar y los resultados que podemos llegar a esperar, sin llamarnos (ni a nosotros ni a nuestros clientes) a engaño, sin esperar más de lo que pueden dar, y sabiendo elegir para cada caso la mejor herramienta.

En el artículo https://www.hispasonic.com/tutoriales/nyquist-muestreo-critico-96khz/38357 se suscitó una interesante discusión en relación con si era o no factible obtener en una realización enteramente digital (sometida a un muestreo a velocidad fija) un retardo que no fuera de valor múltiplo exacto a la duración del periodo de muestreo. Como prometí presentar una justificación algo más profunda vamos con ello (sólo para los más sesudos ingenieros). Viene al caso incluirla aquí, porque tiene que ver con la interpolación necesaria para crear los retardos fraccionarios en un sistema digital.

Disculpad todos los demás el que abrume aquí con las matemáticas. No se trata para nada de que vayamos a iniciar en Hispasonic un curso de procesado digital de señal (no creo que tenga suficientes seguidores). Sólo (por una vez y sin que sirva de precedente) de intentar dar una respuesta a una duda que se planteó y que exige acudir a este nivel de detalle. Los demás sencillamente ‘desconectad’ aquí. Es un nivel que sólo debería interesar a las personas que quieran implementar un retardo digital (del tipo v3 para más señas, es decir, que admita retardos fraccionarios y variables).

La función del filtro de reconstrucción en un D/A es ‘reconstruir’ todos los valores que median (en cualquier instante) entre las muestras para así recuperar la señal original. Y esa reconstrucción para ser perfecta debería basarse en un filtro con forma (respuesta impulsiva) de sinc. El interpolador ideal se basa en el uso de la ‘sinc’, tal como es bien conocido en la teoría del muestreo (el filtro de reconstrucción es un paso bajo ideal –pulso cuadrado en frecuencia- que corresponde a una respuesta impulsiva en forma de sinc).

En definitiva partiendo sólo de las muestras (y haciendo uso del reconstructor o interpolador ideal -la sinc-) podríamos obtener cualquier valor de la señal intermedio entre dos muestras cualesquiera. Como caso particular de lo anterior, un sistema digital (que sólo dispone inicialmente de las muestras de la señal en los instantes de muestreo) puede calcular el valor de la señal en cualquier punto intermedio entre dos de las muestras (y hacerlo con precisión y exactitud). Pero no es trivial el cómo se obtiene, así que veámoslo.

Primero lo demostramos con fórmulas (en el dominio de la frecuencia, resulta más sencillo) y luego lo pintamos en el dominio del tiempo para que se entienda mejor cómo se implementa un retardo fraccionario íntegramente digital (implementación que se realiza típicamente en el dominio del tiempo).

Una demostración (en el dominio de la frecuencia)

El muestreo de la señal x(t) se formula como multiplicarla por una secuencia de pulsos p(t), lo que en el dominio de la frecuencia equivale a

X(w)*P(w) (donde * indica la operación convolución)

Aparecen las bien conocidas réplicas de X(w) en los sucesivos múltiplos de la frecuencia de muestreo:

Supongamos ahora la señal xd(t)=x(t-d), que es una versión ‘retardada’ de x(t), y que puede modelarse como resultado de pasar x(t) por un filtro de retardo (delay) puro d(t), que es un paso todo con respuesta en fase de tipo pendiente constante D(w), lo que ilustramos así (a la salida del filtro tendríamos el producto de X(w) por D(w)):

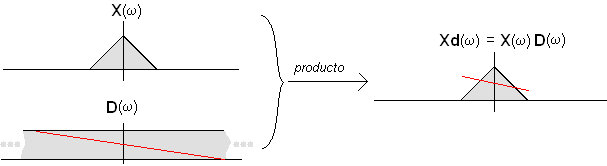
Si muestreáramos xd(t) obtendríamos una versión muestreada de la señal original sometida a retardo que en el dominio de la frecuencia sería

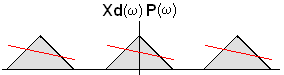
Y sabemos que Xd(w)*P(w) = [X(w)D(w)] *P(w)

Nuestro problema se centra en cómo obtener esta señal (versión muestreada de la señal retardada) sin necesidad de acudir al dominio continuo, manteniéndonos en el dominio discreto.

Para ello vamos a plantear primero el paso al dominio continuo, para luego deshacernos de ese paso.

Si introducimos el filtro de reconstrucción para recuperar xd(t) a partir de su versión muestreada (filtro que llamaremos r(t) con transformada R(w) y que sería un filtro con respuesta impulsiva en sinc y respuesta en frecuencia cuadrada), tenemos

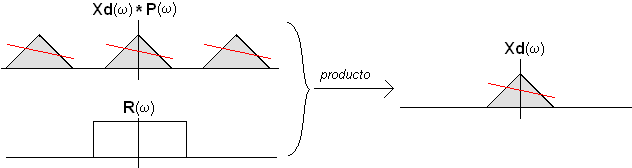
Es decir Xd(w) = [ [X(w) D(w)] *P(w) ] R(w)

Las propiedades de los sistemas lineales permiten reagrupar así

Xd(w) = [X(w) *P(w) ] R(w) D(w)

Pero R(w) D(w) equivale a concatenar el filtro sinc R(w) y el filtro retardo puro D(w), con lo que podemos representarlos como un único filtro Rd(w), que sería una versión retardada del filtro de reconstrucción (es decir, una sinc retardada).

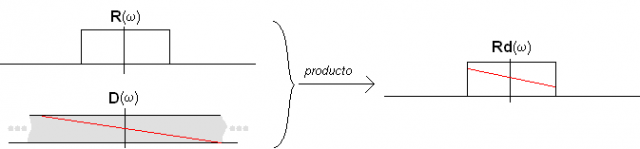
Ese filtro de sinc retardada puede aplicarse a X(w)*P(w) (la versión muestrada de la señal original sin retardo) para obtener la señal retardada en tiempo continuo (en definitiva estamos combinando el retardo y la reconstrucción en un único filtro).

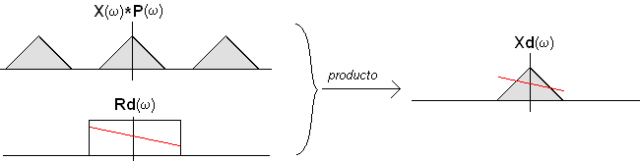
Por tanto un filtro de reconstrucción que permite a partir de las muestras de x(t) obtener la señal retardada xd(t) no es sino el que tiene por respuesta impulsiva una sinc retardada (desplazada en el tiempo).

Si deseamos realizar ese filtrado enteramente en el dominio discreto (obteniendo una versión discreta de la señal retardada en vez de una continua), estaríamos usando un filtro Rd(w)*P(w) aplicado sobre X(w)*P(w), con lo que obtendríamos la multiplicación de X(w)*P(w) por Rd(W)*P(w) que es idéntico en forma al espectro que esperábamos para Xd(w)*P(w)

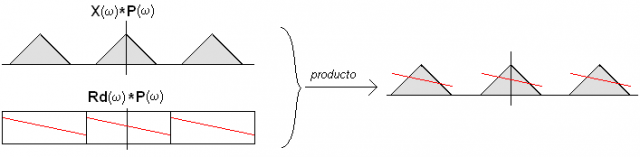
O sea, usando una sinc retardada discreta como reconstructor, podemos obtener una versión muestreada de la señal sometida a retardo, partiendo de sus muestras sin retardo. Y eso sea cual sea el retardo (aunque sea ‘fraccionario’). Como estamos hablando de una realización discreta y la sinc es decreciente hacia ambos lados, es posible el cálculo finito y suficientemente aproximado (obviando las colas de la sinc cuando ya su valor sea suficientemente próximo a cero).

Es decir podemos obtener xd[n] (la señal retardada muestreada) sin más que realizar la convolución de x[n] (la señal original muestreada) con la versión discreta de del filtro rd[n] (que sería la forma sinc desplazada por el valor del retardo), recortada en su duración para permitir un cálculo finito.

Ilustración (en el dominio del tiempo) para entender cómo se realiza el cálculo

Aquí tenéis una señal continua x(t) en verde y marcadas con puntos gordos sus muestras (supuesto un reloj de muestreo definido por los trazos en rosa). Voy a llamar x[n] a esas sucesivas muestras (sólo represento 5 de ellas) que no son sino los valores de x(t) para aquellos instantes t que coinciden con múltiplos del periodo de muestreo (Ts) a su vez inverso de la frecuencia de muestreo fs. Voy a suponer que mi interés está en el punto central y sus alrededores (así que a ese punto central le hago corresponder n=0).

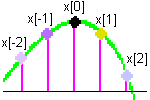
La reconstrucción ideal exige filtrar con el filtro de tipo ‘sinc’, es decir, exige realizar la convolución con la sinc. Dicho de otra forma: si queremos reconstruir a partir de las muestras la señal original (que es continua, no muestreada), hay que replicar la forma ‘sinc’ en cada una de las muestras y combinarlas. Cada muestra se ‘sustituiría’ por una forma ‘sinc’ (con la altura definida por el valor de la muestra) y todas esas ‘sinc’ se sumarían. El resultado sería la señal original continua reconstruida a la salida del D/A.

Por ejemplo la réplica que correspondería a la muestra central de ese grupo de cinco sería la línea negra (en realidad la sinc tiene duración mayor, pero aquí la estoy recortando para no complicar más el dibujo)

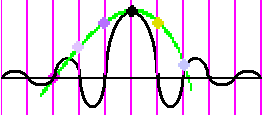
Y si colocamos las otras réplicas necesarias para ese grupo de cinco muestras (cada una con su color para distinguirlas) tenemos

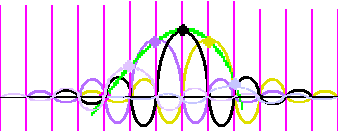
La suma de todas esas sincs es exactamente la señal original (la señal verde). Es un resultado elemental de teoría de procesado de señal. Al menos lo sería si usáramos la duración completa de la sinc (sin recortar) y colocáramos una en cada muestra (no sólo en este grupito de cinco muestras). Estos ‘recortes’ hacen que sea una solución aproximada.

Lo que acabamos de hacer es un interpolador de orden 5 basado en sinc recortada, mucho mejor que la simple interpolación lineal (la de la línea recta entre dos puntos), porque esta interpolación sí puede aproximar mejor la curvatura de la señal entre cada par de muestras (tanto más precisamente si en lugar de orden 5 eleváramos el orden). Aún sería mejor usar interpolación de mayor orden, implicando más muestras.

A la vista de lo anterior, si somos capaces de recrear x(t) para cualquier punto intermedio (para cualquier valor de t) ¿qué nos impide ‘adivinar’ a partir de las muestras disponibles el valor que habría en la posición correspondiente a 0,5 muestras o a 0,1 muestras? Es una operación factible. El problema de obtener una muestra intermedia entre otras disponibles (de obtener retardos fraccionarios) puede resolverse sin abandonar el entorno digital.

Cuando se trata de reconstruir justo el valor correspondiente al instante de una de las muestras, todas las contribuciones son nulas (cruzan por cero) salvo la que corresponde exactamente a esa muestra (lógico: esa muestra es ‘autosuficiente’ para describir el valor de la señal en ese punto, no necesita nada más).

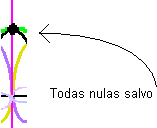
En los puntos intermedios entre dos muestras aparecen contribuciones de todas las muestras, con un peso que depende cómo de lejos están (el valor exacto de ese peso queda determinado por la forma de la sinc). La solución pasa por sumar el valor de todas esas sinc evaluadas en ese punto concreto.

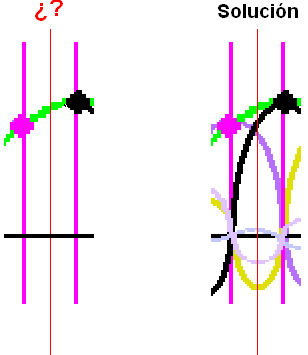
Los pesos que hay que usar al combinar los valores de las muestras para realizar la interpolación no son sino los valores de la forma sinc muestreada con ese retardo ‘d’ que deseamos obtener.

Así, para retardo cero, las muestras que han de salir son las mismas que hay en la entrada, y de hecho los valores de la sinc por los que ha habido que multiplicar las muestras han sido estos (tal como dijimos antes, todos nulos salvo el central):

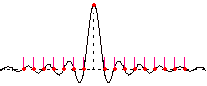
Para retardo de media muestra los valores que tendríamos que usar como ‘pesos’ para combinar los valores de las muestras de señal disponibles serían