Loudness o sonoridad y presión sonora (I): percepción del nivel de sonido
- Presión sonora: significado, unidades y umbrales de audición
- Loudness vinculado a ¿amplitud o energía?
- La sensación de loudness no es instantánea, sino ‘promedio’
- El concepto de ‘envolvente’
- La rectificación: el nivel no es bipolar
- El promediado y la duración del ‘ventana de observación’
- Resumiendo
- Una aclaración: energía vs potencia
A veces pensamos en el loudness (o sonoridad) un tanto ciegamente, aplicando sin mucha reflexión los dBSPL. Con una cadena de tutoriales buscamos entender y no sólo operar con el loudness, como continuación de nuestras entregas sobre acústica y electrónica.
Presión sonora: significado, unidades y umbrales de audición
[Índice]El sonido corresponde a las variaciones de presión en el aire, mediante compresiones y rarefacciones en torno a la presión atmosférica. A la postre no necesitamos saber mucho de presión y sus unidades, porque nos hemos inventado algo (el nivel de presión sonora y los dBSPL) para tener una escala útil y sencilla de entender y aplicar. Pero eso no impide que nos interesemos por observar algunas características curiosas que asoman cuando pensamos en términos de presión y sus unidades.
La presión usa como unidad el Pascal (Pa). Por ejemplo, la presión atmosférica ronda aproximadamente los 100.000 Pa, en función de las condiciones climáticas, la altura sobre el nivel del mar, y otras condiciones.
Respecto a ese valor las variaciones que causan los sonidos son realmente pequeñas. La variación de presión en los picos de aquellos sonidos que ya comienzan a infligir dolor es de tan solo 20 Pa, mientras que los sonidos apenas perceptibles desarrollan una excursión de sólo 0,00002 Pa, también escrita como 20 x 10-6 Pa, valor de presión conocido como umbral auditivo.
Siendo como es irrelevante la presencia permanente de 100000 Pa ’atmosféricos’ e interesándonos sólo por las variaciones en torno a ese valor, se ha definido la presión sonora como aquella que resulta de retirar en la medida la aportación de la presión atmosférica, haciendo que el rango de esta así llamada presión sonora se extienda de 0,00002 a 20 Pa, o lo que es lo mismo de 20 x 10-6 Pa hasta 20 Pa. No es nada despreciable la extensión que supone, con el mínimo de presión sonora detectable un millón de veces por debajo de aquel valor que produciría dolor (y que por tanto es a efectos prácticos una cota máxima que no conviene rebasar). El uso del micro Pascal o μPa, permite reexpresar el umbral auditivo como 20μPa con mayor comodidad.
| Presión sonora | |
| Umbral de audición | 20 μPa |
| Umbral de dolor | 20 Pa |
Se trata de valores medios usados como referencia, con diferencias para cada persona y también en función del tipo de sonido, su forma de onda y su frecuencia.
Existen sistemas de reproducción audio que van mas allá del nivel de dolor, pero lo normal será que no se usen tan cerca de los oyentes como para que les llegue esa gran presión. Así no es extraño que en la inmediata proximidad a un altavoz o un cluster las presión pueda ser incluso peligrosa/dañina. Pero estarán tan alejados de la audiencia que lo que llegue a esta será un nivel más tolerable. No debe extrañarnos por tanto que muchos sistemas de reproducción especifiquen que son capaces de generar niveles de presión sonora a un metro (que es la distancia a la que muchas veces se dan estas características en las especificaciones) muy por encima no ya de umbrales de dolor sino incluso llegando a valores capaces de provocar daño instantáneo en el tímpano.
Loudness vinculado a ¿amplitud o energía?
[Índice]Lo de los pascales y la presión sonora nos habla de cómo medir una característica física, pero no nos dice cómo sentimos/percibimos el nivel en las señales audio.
Es interesante destacar desde un primer momento que, cara a la percepción de un sonido como fuerte o débil, nuestra audición reacciona más bien al cuadrado de la presión. Para que notemos la sensación de oír un sonido de doble fuerza (una apreciación subjetiva, que se ha caracterizado estadísticamente con pruebas y tests con personas) basta que el cuadrado de la presión se haya doblado, no hace falta que la amplitud de la presión se doble, no necesitamos llegar a doblar la presión.
Hemos prometido no ser muy ‘científicos’ ni exigentes en lo teórico-matemático, así que demos por bueno que esa percepción ligada al cuadrado del valor de la amplitud habla de que nuestro oído siente la ‘energía’ y no la ‘amplitud’. [En física la energía y la potencia son magnitudes guardan siempre una relación cuadrática con la amplitud del campo -en nuestro caso con la presión sonora-, así que a veces veréis hablar de energía o potencia de forma semejante: aunque son cosas distintas, son parientes cercanas. Al final tenéis un complemento sobre esta cuestión].
Lo que quiero destacar es que no sentimos la amplitud que vemos en el osciloscopio ni la que representa la gráfica de la señal en un DAW. Si bajamos a la mitad esa amplitud no oímos la mitad de fuerte, la oímos unas 4 veces más débil (2 al cuadrado).
Hablamos de loudness o sonoridad para indicar esa ‘sensación’ de la fuerza o intensidad sonora tal como la percibimos los humanos, y que globalmente vinculamos con la energía, no con la amplitud de la señal sonora (digo ‘globalmente’ porque hay también diferencias en cómo de fuertes oímos los sonidos en distintos rangos de frecuencias y otras cuestiones que presentaremos otro día).
Por tanto, partiendo de un sonido de presión sonora X (Pa), conseguir una sensación de sonido cien veces más intenso (en energía) exigiría sólo diez veces esa presión (amplitud) de partida, es decir 10X (Pa), no 100X (Pa). De forma semejante conseguir la sensación de sonido doblemente intenso (una sonoridad doble) requeriría una presión sonora de 1.41X (Pa), porque la raíz de dos es 1,4142…
Desde esa perspectiva, el recorrido ya de por sí amplio de un millón de veces que separa la mínima y la máxima presión sonora (los 20micropascales y los 20 pascales), se convierte al elevar al cuadrado los extremos para obtener los correspondientes valores de potencia en nada menos que un millón de millones de veces más potencia. Esa es la apabullante diferencia de sensaciones que podemos llegar a encontrar en nuestra percepción de los sonidos. Un recorrido que, por ser tan extenso, se vuelve difícil de manejar numéricamente, por lo que se han concebido otras representaciones más compactas, en concreto se aplican medidas en dB (decibelios). [Sobre los dB hemos presentado ya varios tutoriales que recordaremos un poco más adelante.]
La sensación de loudness no es instantánea, sino ‘promedio’
[Índice]Otra cuestión que hemos de recalcar en cuanto a la percepción de la sonoridad: está vinculada al comportamiento global de la señal, no a su detalle. Son los sonidos señales oscilantes, como por ejemplo lo es una sinusoidal. Pero no tenemos sensación de que su sonoridad varíe durante las evoluciones de cada ciclo, sino sólo de forma más agregada, sólo sensible al promedio. Nuestra escucha de las variaciones microscópicas / de detalle se expresa en las sensaciones de timbre, no en las sensaciones de nivel. Nuestra escucha del nivel es siempre macroscópica por comparación. Algo que nos lleva de forma natural a presentar el concepto de envolvente, y también a precisar qué significa una medida RMS o Root Mean Square, unas siglas frecuentes en audio.
El concepto de ‘envolvente’
[Índice]Una representación cuya escala temporal sea de muy pocos milisegundos o pocas decenas de milisegundos nos permite ver el detalle exhaustivo de la señal, cada una de sus subidas y bajadas de nivel/presión. Pero cuando representamos la señal a otras escalas más amplias (cuando hacemos un ‘zoom out’) este detalle necesariamente se pierde, y lo habitual es que se represente algún tipo de (así llamada) ‘envolvente’: una traza del contorno general, pero ya sin el detalle al completo. Perdemos la visión de los ciclos individuales de subida/bajada de la presión y nos quedamos sólo con una referencia global o promedio de nivel.
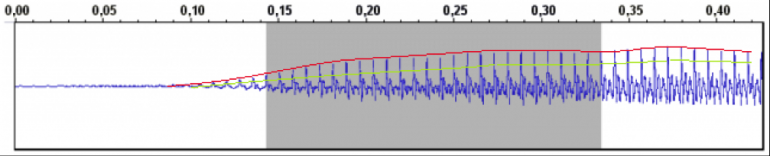
Algo semejante sucede con nuestra sensación de la fuerza o nivel de los sonidos. Sólo la sentimos, como decíamos, en una especie de promedio, de tendencia. Dicho nivel promedio puede verse como la línea roja creciente en esta gráfica (que esencialmente representa un contorno elaborado a partir de los picos de la señal) o como la línea verde (que traza una especie de nivel promedio). Son sólo dos ejemplos de cómo podríamos intentar concebir y representar una idea del comportamiento global de nivel.
Esa figura anterior ya manifiesta la posibilidad de diferentes formas de considerar la evolución ‘global’. Mientras que la señal instantánea y detallada está definida de forma única, a la hora de caracterizar su envolvente podemos decantarnos por diferentes representaciones. Tanto la línea roja como la verde nos informan de una señal que manifiesta un nivel creciente a lo largo del tiempo y que finalmente parece estabilizarse. Pero son dos contornos distintos.
En la construcción de esos contornos o envolventes de una señal intervienen dos pasos: una rectificación primero y algún tipo de promediado después.
La rectificación: el nivel no es bipolar
[Índice]El nivel que sentimos sólo distingue en un recorrido absoluto fuerte/débil, no hay una sensación de nivel 'negativo'. Pese a que la señal original es bipolar, no tenemos sensación de oír dos niveles diferentes sino sólo uno. Aunque la señal sea tan asimétrica como la que muestra la anterior imagen, oímos 'un' nivel.
Dicho desde una perspectiva más formal, sabiendo que escuchamos en función de la energía, el signo de la señal nos da igual: la energía usa una versión cuadrática de la amplitud y por tanto siempre positiva. Como consecuencia una cuestión que asoma en todas estas representaciones ‘de envolvente’ es la irrelevancia de mantener el carácter bipolar que originalmente tiene la señal.
Esto lleva a considerar la llamada ‘rectificación’ de la señal como primer paso en la obtención de la envolvente. Hay dos formas de rectificación: de media onda y de onda completa.
- Rectificación de media onda implica anular la señal por debajo del nivel cero y quedarnos sólo con la parte positiva. Era un cambio muy sencillo desde el punto de vista de la electrónica, y generalmente el impacto que causa sobre la estimación del nivel no es grave. Pero incluso el estándar para los VU meter hablaba de rectificar en onda completa, no en media onda.
- Rectificación de onda completa implica invertir la señal negativa para que tome valores positivos. Es equivalente a quedarnos con el ‘valor absoluto’ de la señal.
Pero además de la cuestión de la rectificación (en la que los sistemas suelen decantarse por la de onda completa, salvo que intervengan razones de coste), está la otra no menos importante.
El promediado y la duración del ‘ventana de observación’
[Índice]Cualquier envolvente implica eliminar detalle y quedarnos sólo con la tendencia. Eso exige tomar alguna decisión sobre la duración del intervalo durante el cual vamos a ‘integrar’ el comportamiento de la señal y esquivar su estructura interna reemplazándola por un valor conjunto. Cuál es la duración o ventana del promediado, el ‘tiempo de reacción’ con el que se producen las evoluciones de la envolvente, importa e impacta mucho en el resultado.
En nuestro caso, con ciclos que llegan a los 50ms en el registro grave, no son extraños tiempos de reacción de pocos cientos de ms. Es el caso por ejemplo de la aguja de los vúmetros, cuya inercia responde aproximadamente con tiempos del orden de unos 300ms.
Tendremos ocasión de hablar en profundidad sobre el efecto de las constantes de tiempo cuando presentemos los compresores y otros sistemas de alteración de la dinámica, en los que el usuario suele poder ajustar los tiempos de ataque y de relajación, a través de los cuales se pueden conseguir resultados muy diferentes. Por ello no ahondaremos ahora mismo en esta cuestión más allá de citar su importancia. De hecho no sólo la duración, también la 'forma' de la ventana impacta, pero por hoy nos basta reconocer que diferentes duraciones provocarán diferentes envolventes, unas más marcadamente globales y lentas, otras capaces de hacer un seguimiento algo más fino y ágil ante los cambios.
Resumiendo
[Índice]- La presión sonora es una medida de amplitud de la señal sonora, en la que no consideramos la presencia de la presión atmosférica sino las excursiones en torno a ella.
- Los umbrales de la audición humana son tales que permiten detectar sonidos con valores de presión sonora desde los 0,00002 hasta los 20 Pascales, un amplio recorrido en el que el mínimo es 1 millón de veces menor que el máximo.
- Pasando a la cuestión de cómo sentimos, percibimos el loudness en función de la energía (no de la amplitud) y siempre de forma agregada/promediada en un amplio tiempo.
- La obtención de la envolvente de una señal implica rectificar y promediar, y admite múltiples maneras de resolver la cuestión.
Como supongo que os habrá sabido a poco la entrega de hoy, no vamos a demorar la aparición de la siguiente, centrada en presentar qué son el valor RMS y el vúmetro. Pero me parecía adecuado asegurar una mirada común sobre estas cuestiones de hoy que impregnarán esa siguiente entrega.
Además para no dejar tan corto de contenidos este tutorial, aprovecho para colaros algo que podéis tomar como opcional. Dado que hemos hablado de que sentimos el nivel audio vinculado a la energía, quería comentar la diferencia energía/potencia. No lo veo esencial para manejarnos en la vida diaria, y de hecho según los países y los libros veréis usar uno u otro término (especialmente en casos como 'energía media' que para algunos es una aberración porque prefieren llamarlo potencia, por ejemplo).
Una aclaración: energía vs potencia
[Índice]Como siempre en esta serie intentaremos no ser muy matemáticos/físicos, pero sí conviene una mención al menos a los parecidos y diferencias entre energía y potencia. A veces los usamos de forma casi indistinta en la vida ordinaria, para horror de los físicos. Y es que energía y potencia no son lo mismo, pero siempre resultan en física de una relación cuadrática con la amplitud, que es el hecho que para nosotros nos interesa destacar y que a veces nos lleva a confundir o usar indistintamente ambos términos.
En ese sentido, si llamamos s(t) a una señal que representa la amplitud o nivel instantáneo de nuestra señal, podríamos pensar en una nueva señal que represente la ‘energía instantánea’ o la ‘potencia’ de esa señal y que sería [s(t)]2 también escrita a veces como s2 (t).
Por ejemplo, en electrónica la potencia (P, vatios) es el producto de la tensión (V, voltios) y la corriente (I, amperios), es decir P= V I. Pero como la ley de Ohm establece entre V e I una relación a través de la resistencia (R, ohmios) descrita como V = I R, podemos llegar a que P = V I = R I2 = V2 / R, expresiones que hacen patente esa relación cuadrática, más allá de la compañía de un factor R multiplicando o dividiendo. Ese producto P = I R era la potencia. Para poder valorar energía necesitamos además introducir el tiempo, pero seguirá tratándose de una relación cuadrática con la amplitud (ya sea medida en tensión –voltios- o en intensidad –amperios-).
Sobre la diferencia entre energía y potencia es bastante evidente este ejemplo: Los 100W indicados en una bombilla hablan de su consumo instantáneo cuando esté alimentada en las condiciones normales de la red de suministro eléctrico (los 220V AC en España). Es la potencia que gasta en condiciones normales de trabajo, la potencia que exige le sea entregada en todo momento para producir luz adecuada. La energía que consume esa bombilla al usarla es el producto de esa potencia que gasta al producir luz por el tiempo durante el que la tengamos encendida.
Lo que quiero destacar es que la medida de energía siempre está referida al total de un tiempo de observación, mientras que la potencia no hay esa presencia del factor tiempo. Una bombilla de 100W de potencia que esté encendida 10 horas al día consumirá 100x10 = 1000Wh de energía cada día, es decir, 1kWh por día (que viene a costar unos 15 o 20 céntimos de euro a precio actual en España). Esa es la energía diaria que consumiríamos.
Otro ejemplo también muy claro es el de la factura de la luz y sus términos fijo y variable: el término fijo es por potencia contratada (cuántos kW queremos garantizar que se nos puedan llegar a servir desde la red) y el término variable es por energía consumida (nos cobran por los kWh que hemos usado realmente: un resultado de integrar a lo largo del tiempo la demanda de energía que efectivamente hemos absorbido de la red). En la energía aparece esa idea de un determinado tiempo de observación: cuánta potencia hemos absorbido de la red durante cierto tiempo. Los 3300W de potencia contratada que muchos tenemos en nuestro contrato de suministro para el hogar hablan del máximo de potencia que vamos a pedir a la suministradora. No indica ningún consumo real, sólo la capacidad de llegar a desarrollar un cierto trabajo o esfuerzo (en este caso llegar a alimentar equipos eléctricos que agregadamente no exijan rebasar ese límite). La mayor parte del tiempo consumimos menos. Sólo si nos pasamos ‘saltan los plomos’ o ‘se va la luz’, como suele decirse.
En consonancia con lo dicho, la potencia tiene unidades de W, mientras la energía aplica unidades basadas en un producto potencia y tiempo, como esos kWh (producto de kilovatios y hora).
Parecería más correcto, desde la perspectiva de las unidades, hablar de potencia (y no de energía instantánea, aunque a veces se vea así dicho) cuando se trata de un valor instantáneo y por tanto sin referencia a una duración o plazo. También sería potencia (W) lo que usaríamos para hablar de un valor pico en el que tampoco interviene el tiempo (como podría ser aquella potencia que puede llegar a estropear un equipo, que sería su potencia máxima admisible –no decimos energía instantánea máxima antes de romperse-).
También oímos hablar de potencia media (y no de energía media consumida) cuando calculamos un promedio de la energía a lo largo de un tiempo, cosa que ilustra este ejemplo: Después de estar encendida 10 horas esa bombilla de la que hablábamos el contador ha subido 1kWh (ha gastado un kWh de energía), lo que indica un consumo medio de 0.1kW, o sea 100W. Un valor que aunque ha sido calculado mediante un promedio temporal de la energía algunos no llaman energía media, sino que prefieren toldar de potencia por aquello de que sería raro llamar energía (aunque fuera media) a algo que tiene unidades de W.