Ayuda con problema matemático/trigonométrico

Auguro muchas visitas a este hilo y un sinfín de respuestas. A ver, tengo una edad para no acordarme ni una mierda de trigonometría y otras mandangas matemáticas, con lo cual el problema que os voy a presentar a lo mejor está chupado, pero se me atasca. La imagen de abajo es una simplificación muy básica de unos planos que estoy intentando hacer, bastante más complejos, pero el fundamento y la respuesta al problema es el mismo

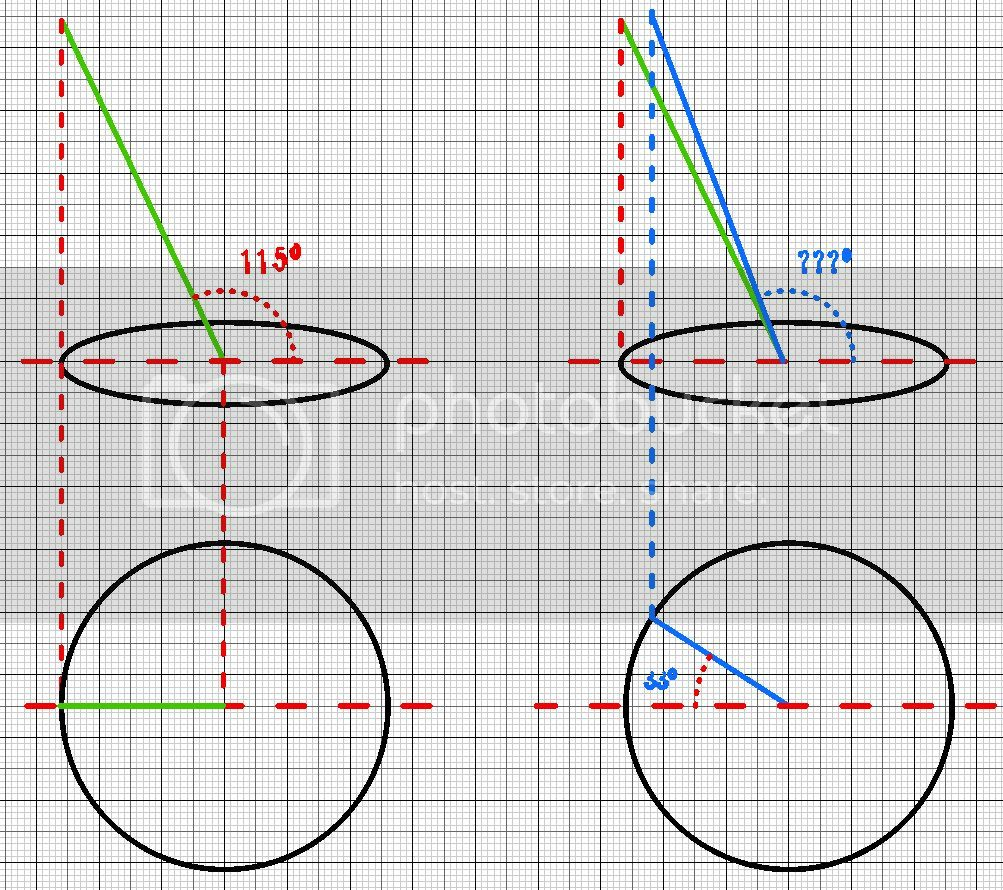
Lado izquierdo de la imagen. Un reloj de sol (círculo negro) con el gnomon (la varilla de color verde) inclinada sobre el plano en ángulo de 115º (65º el ángulo interno). Lado derecho, imaginad que giro el reloj de sol 33º (o los que sean) sobre su eje. El ángulo aparente de la varilla (ahora en azul, dejo la verde para que se vea ese cambio) es ahora menor de 115º (o mayor de 65º). Lo que quiero es calcular ese nuevo ángulo e imagino que habrá que tirar de trigonometría, pero como digo, ni flores. Pues eso, echadme una mano, payos

tricky2k escribió:

El ángulo aparente

supongo que ahí está la clave, el cambio del ángulo es más un efecto óptico de la perspectiva que un cambio real

a bote pronto se podría tirar de regla de tres

si a 0º (sin girar el reloj) el ángulo es de 115º y a 90º (la varilla la vez de frente) el ángulo es de 90º puedes sacar una aproximación, no se si habrá una forma más precisa.

¿Cuánto mide la varilla o cuál es el radio del círculo?

A veces en el trabajo tengo que tirar de trigonometría, tampoco es que tenga mucha idea pero me surgen unas dudas con el problema.

tricky2k escribió:

El ángulo aparente

Al girar el reloj (sobre su eje o base entiendo) el ángulo no debería de variar...o con lo de aparente te refieres a que en la representación en dos dimensiones si varía.
Creo que para sacarlo habría qu eempezar por tener la medida de la hipotenusa (gnomon) y los catetos : uno sería el radio del círculo que forma la base del reloj (si es que el gnomon esta centrado) y el otro sería la altura que hay desde la base hasta la punta del gnomon.
Sin esos datos creo que está dificil. Por lo menos para partir de el teorema de Pitágoras que es la base de estos rollos trigonométricos.

https://es.wikipedia.org/wiki/Teorema_de_Pit%C3%A1goras

Conociendo al menos dos de estos datos ya se podría empezar a pensar en como sacar el ángulo jugando con triángulos rectágulos y Pitágoras...complementarios etc...

A no ser que alguien más puesto tenga otras fórmulas para sacarlo. Yo es por donde empezaría.

#2 Ahí está la respuesta, en el gif que has puesto tú mismo en el hilo de gif animados. Las cosas no son lo que aparentan...

No se si he comprendido bien el problema. Pero si lo he comprendido siempre los dos angulos suman 180 grados, tanto si hablamos del plano de la esfera del reloj como si hablamos del plano sobre el que esta el gnomon. Sabiendo cual es uno de los angulos podemos saber cual es el otro porque entre los dos suman 180, tanto en el plano de la esfera ( como parece sugerir el dibujo de la parte inferior derecha) como en el caso del plano sobre el que esta el gnomon ( como parece sugerir el dibujo de la parte superior derecha)

(Perdon por escribir sin acentos, no se que pasa con el teclado del movil que no los escribe)

Supongamos círculo de radio a y longitud de gnomon c.
Lo tenemos representado a la izquierda en una vista de planta (arriba) y perfil (abajo).

Giramos el círculo 33º (o el gnomon, lo mismo da). Lo tenemos representado a la derecha. El triángulo cambia la base a => a' y los ángulos. La clave aquí está en que visto de perfil, la altura b no cambia.

Para resolverlo: http://www.vitutor.com/al/trigo/tri_12.html

conociendo la hipotenusa (c) y un cateto (b), adjunto fórumulas.

No me hagáis ni caso.
La sobremesa es para la siesta.
El segundo c es un c'. Podemos calcular a' y así tendríamos el valor de la hipotenusa c y el cateto a'.

tricky2k escribió:

Lo que quiero es calcular ese nuevo ángulo

#1

En la imagen de la derecha el dibujo de arriba dibuja un ángulo que corresponde a un plano ( vertical o alzado) mientras que el de abajo, el ángulo corresponde a otro plano( horizontal o planta)
Para plantear un problema se debe entender a qué plano corresponden los ángulos cuya medida se busca.
Supongo que lo que se busca es el ángulo aparente que formaría al ver de frente el círculo ( figura inferior derecha, planta).

#6

Pero al no ser 115 ya el ángulo y no tener ese dato creo que lo de los ángulos complementarios ya no sirve ya que habría dos incognitas, y la única certeza sería 180 grados.
No sirve por si solo, pero será de ayuda junto con pitágoras.
#1

Otra opción es que busques a alguien que trabaje o sepa usar y tenga AutoCad y te lo saca en un periquete. Aún así necesitarás los datos de hipotenusa y catetos (al menos uno).
Menos satisfactorio personalmente eso si.

Creo que tienes una variable compleja ahí. Y es el hecho de que giras el reloj x grados (33) en la planta. Tendrás que representar eso de manera exacta también en el alzado (no solo en la planta) para conocer la variación exacta que se produce al hacer el giro en el alzado y encontrar la medida de tus muevos catetos e hipotenusa.
Esto AutoCad lo hará en un momento, de nuevo.

Por curiosidad, ¿para que necesitas este dato?. Porque como ya hemos dicho varios al girar solo varía en el alzado de la representación en dos dimensiones no en la realidad. ¿Tiene que ver con la proyección de la sombra del reloj solar?.

#7

Joder, los senos y cosenos. Pues con eso si consigue representarlo en alzado de manera exacta lo tiene.

Porque en planta solo como propones en el dibujo no lo veo.

Entiendo que hay que ver el plano de la circunferencia totalmente abatido. De ese modo, la hipotenusa (gnomon) tiene siempre el mismo valor durante todo el giro, y el único problema es calcular cuál es la disminución del radio en el recorrido de esos 33º.

En trigonometría, la circunferencia es goniométrica, por tanto, el radio toma como valor la unidad, sin magnitud.

A partir de ahi calculáis los lados del triángulo rectángulo inicial, la altura del abatido y luego la resultante aparente del radio inicial de nuevo en el primer triángulo donde la altura del segundo lo corta. Fácil.

A mí me da una variación mínima respecto al valor inicial: 67º aprox. con lo que el ángulo que buscas quedaría en 113º.

Comprobad los cálculos porque para esas cosas no me fío mucho de los míos.

¿Ves lo que te digo? Repasando los cálculos me da un ángulo de 69,18º, con lo que el suplementario se queda en 111º aprox.

Endre escribió:

Entiendo que hay que ver el plano de la circunferencia totalmente abatido.

Esto es importante definirlo, también es lo que asume #7 , es la forma más fácil de resolverlo porque se reduce todo a un problema bidimensional, (asumiendo también proyección cilíndrica).

Si no, la cosa se complica un pelín, habría que definir qué tipo de representación se está haciendo, definir un factor de fuga en profundidad...

vagar escribió:

Si no, la cosa se complica un pelín, habría que definir qué tipo de representación se está haciendo, definir un factor de fuga en profundidad...

Eso es lo que yo he entendido, porque si no no veo el problema.

Endre escribió:

Entiendo que hay que ver el plano de la circunferencia totalmente abatido.

Pero si lo ves de esa manera, en planta (es lo que ntiendo por abatido), ¿que es lo que cambia al girarlo 33 grados?

Volvemos a lo de antes. Si tu giras un pieza tridimensional de esas características el ángulo no cambia de ninguna de las maneras. El angulo solo cambia en la representacion del alzado (dos dimensiones) no en la figura real (tridimensional).

Asi que algo se me escapa en la cuenta que hace #12 . Que seguramente sea falta de conocimientos por mi parte.

Que por cierto, el alzado que plantea plantea #1 supongo que lo ha hecho para que se entienda que la base es circular. Porque en un alzado la base circular se vería representada como una linea horizontal sin más, no un escorzo de un circulo (la elipse del dibujo).
A no ser que la representación sea un escorzo lo cual es rizar el rizo.