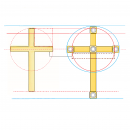
Tio Harpo Molon escribió:Si tú eres el observador y te encuentras mirando de frente ese reloj de sol, habrá dos puntos en los cuales variará una de las dimensiones del triangulo equilátero.
Yo no veo por ninguna parte un triángulo equilátero. Si vemos el conjunto frontalmente, hay un triángulo rectángulo, cuyos catetos miden 1 y 2,144 respectivamente al tomar el radio de una circunferencia goniométrica. Los ángulos son 65º, 25º y 90º, obviamente.
Al girar 33º, la hipotenusa sigue teniendo el mismo valor, porque la perspectiva es despreciable a efectos matemáticos. El error inducido en el cálculo probablemente va a ser mayor que el efecto de la perspectiva.
El arco que recorre el movimiento de la hipotenusa queda circunscrito en un triángulo isósceles (dos lados iguales, formados por el radio) y una base, cuyo valor calculamos partiendolo entre dos y trabajando con dos triángulos rectángulos.
La idea es calcular el lugar donde el cateto vertical cortaría al radio de la circunferencia, disminuyendo su valor inicial. Y eso se obtiene abatiendo el triángulo isósceles y buscando el punto donde ese cateto hace ángulo de 90º con el lado opuesto.
A partir de ahi, un poco más de trigonometría para calcular los diferentes ángulos y lados y ya está.
El radio aparente queda en 0,84, y de ahi, el ángulo es 69º.