Los secretos musicales I. El número de oro

Bobby escribió:

0.9/0.10= 0.9

Creo que acabas de descubir la aritmética Bobbyana, propongo una nominación a la Medalla Fields. Esto demuestra lo importante que es ser creativo, romper moldes y escapar del rancio discurso de los caducos cánones establecidos.

Tienes razón me sale 9.
La segunda lista es un copia pega de la primera añadiendo sólo los 0 con decimales. He calculado los 5 primeros y el último y con la emoción se me ha colao el
0.9/.10 que es igual a 9. Me has cortado un poco el rollo ahora lo repasaré todo otra vez. Pero las fracciones primeras de la primera lista cuadran con notas...

Bobby escribió:

con la emoción se me ha colao el
0.9/.10 que es igual a 9. Me has cortado un poco el rollo

No me hagas caso y déjate guiar por la emoción, ¿qué más da lo que digan las matemáticas? Sé libre y vuela.

Mira lo que acabo de descubrir sobre el número Bobby:

B = 0,99999...
10 x B = 9,99999...
10 x B - B = 9,99999... - 0,99999...
9 x B = 9
B = 9/9 = 1

Así que Bobby es el número 1.

¿Os gustan las matemáticas? A ver si descubrís el factor secuencial de esta serie. A ser posible sin mirar en internet.

1
11
21
1211
111221
312211
13112221
1113213211
31131211131221
...

Que conste que el número B=Bobby era coña. Sabía que soltando alguna gorda se revolucionaría el asunto.
Seguro que la progresión ya está inventada hace siglos.
Un abrazo

#33
B= 0.99999999...
10 x B = 9.99999999...
10 x B - B = (10 x B) - B = 9
9 x B = 8.999999....
B = 8.999999... / 9 = B

Ha sido un post trampa

Bobby es uno más.

1/2 Octaca justa
2/3 Quinta mayor
3/4 Cuarta justa
4/5 Tercera mayor
5/6 Tercera menor
Es correcto esto ? Lo he sacado de una web pero no me fío.
y qué sería
6/7
7/8
8/9
9/10
10/11
Y
11/12 ?

#34
No lo saco ni con internet

Podrias hacer tu mismo el experimento:

Por ejemplo, tomando la primera relación 1/2. Genera una onda senoidal (con algun generador de ondas) de frecuencia 110Hz (un La). Luego, genera otra onda de el doble de frecuencia, 220Hz. Si luego escuchas estas ondas a través de un afinador, verás que obtienes un intervalo de una octava.

Puedes hacer lo mismo con la relación 6/7. Seria 6x110Hz = 660Hz y 7x110 = 770Hz. 660Hz es aproximadamente un Re# algo desafinado, 770Hz es aproximadamente un Fa. Ahora que los músicos me corrijan: El intervalo entre re# y fa seria una segunda mayor?

De hecho si usas la formula:

-12*log2(RELACION) = distancia [semitonos]. Ejemplos

-12*log2(2/1) = 12 (octava)
-12*log2(2/3) = 7.02 (quinta mayor)
-12*log2(3/4) = 4.98 (cuarta justa)
-12*log2(4/5) = 3.86 (tercera mayor)
-12*log2(5/6) = 3.16 (tercera menor)
...

EDITO: log2 denota el logaritmo en base 2. Si tu calculadora no admite log2(x) puedes aplicar la propiedad del cambio de base log(x) / log(2)

Tiene buena pinta. Esperemos que un profesional lo corrobore y de nombre a
6/7
7/8
8/9
9/10
11/12
Si lo hay.
Teniendo en cuemta que tus comentarios son de profesional.

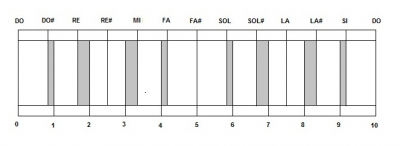
Os subo el primer dibujo antes de ponerle asociaciones.

Bobby escribió:

No lo saco ni con internet

Es una cuestión de pensamiento lateral. No se trata de una serie matemática solamente sino de una serie gramatical también.

Un uno
Dos unos
Un dos y un uno
etc

#43 De las fracciones que mencionas, realizando el mismo calculo que he citado, la única que da un resultado suficientemente próximo a un numero entero de semitonos para que se pueda considerar un intervalo musical, es la fracción 8/9:

6/7 -> 2,668709056 semitonos
7/8 -> 2,3117409353 semitonos
8/9 -> 2,0391000173 semitonos (segunda mayor)
9/10 -> 1,8240371213 semitonos
11/12 -> 1,50637058 semitonos

Saludos

Te he estado leyendo en varios foros Endre y veo que este tema te apasiona. Es una pena que la mayoría de los links del foro antiguo numero Phi no esten ya operativos.
Yo he caído por los números gracias a Cassini y también me apasionan mucho, desde lo que da mi visión algo corta de las cosas claro. Esta asociación se me ha ocurrido gracias a Mikolópez. Que me expuso ayer dos tablas parecidas en el hilo de los sentimientos.
A mí me ha sorprendido encontrarla y me he sentido hoy un poco Einstein. Espero que os halla hecho gracia sino almenos halla abierto el apetito de la curiosidad. A parrir de aquí no sé que me va a salir pero como dice Igarrido: vuela alto. En mi curro dicen lo mismo con la coletilla de que después la ostia será mayor.
Bueno, me pongo con el paint. Aver si esta noche os subo algo chulo.