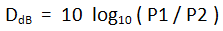Duda clásica con decibelios: ¿doblar suma 3 o 6 dB?
La fórmula que define a los dBs y algunos ejemplos de cálculo mediante dB se publicaron en Hispasonic tiempo atrás en otro artículo. En los comentarios que allí surgieron apareció una duda clásica: el problema de si duplicar se indica con 3dB o con 6dB. Por cierto, si no tienes claro qué son los dB quizá te guste leer esta explicación para músicos sobre los dB, de la que esta entrega es continuación.
Los dB hablan de potencia
[Índice]Potencia y amplitud son cosas diferentes. Cuando se definieron los dB se hizo pensando en usarlos para describir la potencia a la salida de un sistema o de un cable respecto a la potencia a su entrada. Esa es su vocación, servir de apoyo para caracterizar relaciones entre dos potencias.
La potencia tiene una relación cuadrática con la amplitud de la señal. Por ejemplo, en electricidad la potencia (los vatios, W) está relacionada con el cuadrado de la tensión (voltios, V), o si se prefiere con el cuadrado de la corriente (amperios, A). No quiero entrar en las fórmulas detalladas y que obligan a considerar la impedancia, pero sí en esa relación cuadrática. Como resultado cuando la amplitud se dobla (2) la potencia de cuadriplica (2x2=4), cuando la amplitud se triplica (3) la potencia crece por un factor de 9 (3x3), o cuando la amplitud crece por 10 la potencia lo hace por 100.
En otros ámbitos existen también definiciones de qué es la potencia y qué variables describen la amplitud, pero siempre se mantiene el que la relación es cuadrática respecto a la amplitud. Por ejemplo la potencia y el campo de una onda electromagnética, o la potencia y la presión acústicas, etc.
La fórmula de los dB para ratios de potencias
[Índice]Básicamente el valor D (en dB) que corresponde a una determinada relación entre dos potencias se describe como:
siendo P1 / P2 el cociente entre dos potencias expresadas en la misma unidad (la que sea, dado que al formar cociente la unidad se hace irrelevante). Típicamente se trata de la potencia P1 a la salida de un sistema o cable cuando atacamos su entrada con una potencia P2. El cociente P1/P2 describe así cuántas veces mayor o menor es P1 respecto a P2 y por tanto la ganancia o pérdida (en potencia) de ese sistema.
En el caso particular de que P1 sea el doble de P2 tenemos
En realidad se trata de una aproximación: doblar corresponde con más precisión a a 3,01029996… dB. Pero en todo caso el resultado es claro: cuando alguien hable de 3dB implica que se duplica la potencia (P1 doble de P2).
Debemos recordar que, de acuerdo a la intención con la que se crearon enfocada 'a potencias', el uso de los dB quiere siempre pensar en términos de potencia. Se desea tener la tranquilidad de que cuando alguien diga que un sistema ofrece 3dB de ganancia se sepa que habla de elevar al doble la potencia (para entendernos los W -vatios-, no los V -voltios- siguiendo con nuestro ejemplo centrado en la señal eléctrica).
Pero no siempre medimos potencias, muy a menudo medimos amplitudes y usamos sus valores, lo que nos lleva al siguiente apartado.
La fórmula de los dB para ratios de amplitud
[Índice]Muy a menudo es más fácil o más habitual medir la amplitud que la potencia. Cuando en lugar de trabajar con valores de potencia el cociente se establece entre dos cantidades referidas a amplitud de señal, para mantener el que el valor en dB hable de incrementos/decrementos de potencia, es necesario adecuar la fórmula. Como las potencias varían de acuerdo al cuadrado de la amplitud, corregimos la fórmula haciendo que el cociente de amplitudes venga elevado al cuadrado. La fórmula pasa a ser (pensemos por ejemplo en voltios: V1 y V2)
Al haber elevado al cuadrado la relación de las amplitudes, nos situamos de nuevo en el terreno de ratios de potencias, no en el de las ratios de amplitud, aunque a primera vista pudiera parecerlo. De esa forma se sigue teniendo la posibilidad de interpretar el valor resultante en decibelios, D, como una expresión de la relación entre potencias.
Las matemáticas permiten reescribir esa última fórmula de esta otra manera (el logaritmo del cuadrado de una cantidad es el doble del logaritmo de dicha cantidad)
Esta es una fórmula también muy habitual para describir los dB, pero en la que hemos de ser siempre conscientes de que al usar el factor 20 nos estamos obligando a usar la relación de amplitudes y no la de potencias como argumento del logaritmo.
¿Son dos fórmulas?
[Índice]Hemos llegado a una aparente dualidad en la definición:
Aunque formalmente parecen dos fórmulas diferentes (con 10 o con 20 acompañando al logaritmo) lo que las unifica es el concebir esa predilección de los dB por mirar ‘potencias’. La fórmula 'primigenia', por así decirlo, de los dB es la primera. Y se acompaña de un pequeño truco para poder estudiar cuántos dB (con significado orientado a potencias) se asocian a un determinado cambio de amplitud: basta sustituir el 10 por un 20, en el sentido que indican esas dos expresiones anteriores.
Son por tanto dos expresiones distintas para un mismo objetivo (caracterizar potencia, siempre) porque parten de juegos de datos diferentes (potencias o amplitudes). Hemos pues de considerarlas equivalentes y prepararnos para entender las consecuencias, que quedan muy bien ilustradas con el típico error/duda de si duplicar se representa con 3 o con 6 dB.
Consecuencias: la duda de los 3 o 6 dB
[Índice]¿Qué sucede cuando lo que se duplica es el nivel de la señal, sus voltios para entendernos? En ese caso V1/V2 es 2, y su cuadrado pasa a ser 4. Con lo que:
Cuando alguien hable de 6dB habla de cuadriplicar potencia (los vatios, en nuestro ejemplo), o lo que es lo mismo de duplicar la amplitud (los voltios, en nuestro ejemplo).
No pocas veces esta cuestión es fuente de cierto lío, así que nada mejor que rematar con un ejemplo que nos ayude a reflexionar e interiorizar esta cuestión y a recordarla con facilidad en el futuro.
Un ejemplo: audio digital PCM y sus 6dB por cada bit
[Índice]Al codificar una señal analógica en forma digital usamos un cierto nº de bits. Adaptamos la amplitud de la señal analógica al fondo de escala del conversor, y confiamos en que la codificación en un rango discreto de valores no le haga mucha pupa.
Los primeros 'samplers' usaban 8 bits, luego tuvimos de 12, después de 16 (la resolución del CD) y hoy en día muchas librerías de muestras vienen grabadas a 24 bits (lo mismo que encontramos hoy a menudo en interfaces). ¿Qué ventaja añade cada bit de más? Cuando tenemos un cierto número de bits, añadir uno más lo que hace es (para un mismo fondo de escala) reducir a la mitad la separación entre los valores codificados. Fijaos que hablamos de niveles, de amplitudes. No de potencias. Cada vez que doblamos (o dividimos) por dos tenemos por tanto un salto no de 3 sino de 6 dB. Y por tanto cada bit nos aporta una ‘mejora’ de 6dB.
Así la representación con 16 bit lineal (como la del CD) permite una calidad de 16*6 = 96 dB. Y con esa misma regla los sistemas a 24 bit son capaces de llegar a sus conocidos 144 dB teóricos (24*6) pero pocas veces vistos en la práctica (dado que otras partes del sistema suelen tener niveles de ruido mayor).
Pero hemos de tener claro que aunque se haya obtenido pensando en términos de amplitud (‘doblar’ el número de escalones y por tanto reducir a la mitad el tamaño del error de cuantización), esos 96dB y esos 144 dB se refieren a una ratio de potencias: la potencia de la señal frente a la potencia del (mal llamado) ruido de cuantización que la acompañará tras el paso a digital (digo mal llamado ruido, porque es más bien una distorsión).
Para no olvidar
[Índice]Remato con una tabla / resumen, de esas que fácies del mantener en la cabeza para manejarnos con soltura por los dB:
| Ratio en dB | Ratio de potencias | Ratio de amplitudes |
| 0 dB | 1 | 1 |
| 3 dB | 2* | 1,41..(raíz cuadrada de 2) (*) |
| 6 dB | 4* | 2 (*) |
| 10 dB | 10 | 3,16..(raíz cuadrada de 10) |
| 20 dB | 100 | 10 |
(*) Recordad que asociar 3dB a duplicar potencia es sólo aproximado, en rigor duplicar potencia implica 3,01029996 dB.
En caso de valores negativos, ya sabéis, invertís la relación: -3 dB implica la mitad (en lugar del doble de potencia) y -20 dB son 100 veces menos potencia o 10 veces menos amplitud.