????
¿Preguntas como se aplica en un filtro? pero si es obvio hombre, mas aun como te respondo sin citar lo que dice el teorema, no la verdad yo por lo menos no se como responderte, lo que no quita que tenga muy clara la respuesta, pero para ti en particular se me hace difícil elaborar una respuesta.
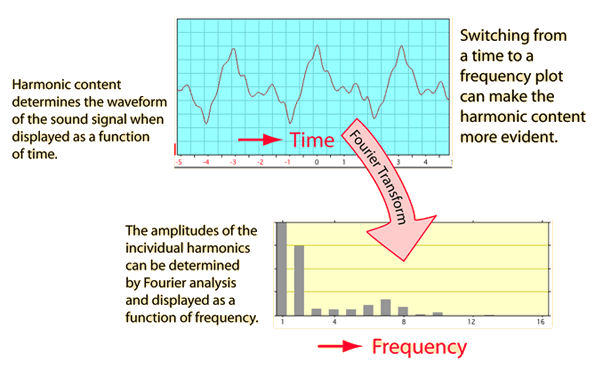
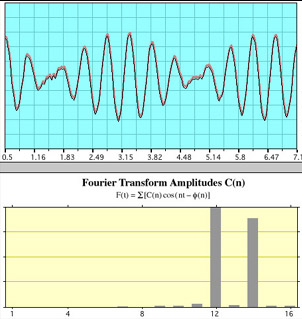
Para el resto de la gente, es fácil, el teorema plantea que toda onda compleja puede ser descompuesta en señales sinusoidales, que quiere decir esto? pues simple, que no importa que tan intrincada sea la distribución de energía en el espectro frecuencial de una onda, puedes entender cada onda como una suma de señales sinusoidales individuales, y, si puedes descomponer una señal en una suma de señales sinusoidales, pues puedes conocer cual es la distribución de la potencia en cada una de esas señales, es lo que hace básicamente la transformada de fourier, llevar la representación de una señal del dominio temporal al dominio frecuencial, el saber que la transformada de fourier hace eso, pues te da la respuesta inmediatamente de como se utiliza en un filtro, o en el análisis de señales.
Yo la verdad es que creo que lo que necesitas es que te vuelvan a repasar el teorema, que no vale aprenderse de memoria el enunciado, hay que interiorizar el concepto, de manera que cada situación real la puedas evaluar en base a los teoremas que conoces. Mi pensamiento es que la educación debe re formularse, las matemáticas no pueden ser consideradas como un fin en si, son una mera herramienta, y la verdad nadie estudia 20 años de como utilizar un martillo para ponerse a hacer muebles. Esto es lo que ocurre cuando se forman teóricos que nunca han necesitado resolver problemas en la practica, que no son capaces de extrapolar lo que estudian en papel a la realidad, no son capaces de traducir el mundo que los rodea a números.
Si tienes una señal real, por ejemplo una voz grabada, en teoría podrías separar esa señal en cada una de sus componentes sinusoidales, si la separas en cada uno de esos componentes eventualmente te es mucho mas fácil suprimir esas componenetes, es lo que hace un filtro.

Por cierto, la misma digitalizacion de señales es consecuencia del analisis de fourier, ya que este requiere llevar una señal continua a a valores instantáneos acotados en el tiempo.

mira la cuestión es que el teorema hace una suma de cálculos bastante complejos, en el proceso de codificacion de la señal, su aplicación en audio es la siguiente:
Entre mayor numero de muestras, 44kHz, 48kHz, el teorema hace un filtrado de frecuencias, especialmente las frecuencias altas.
Es decir que el oído humano comprende un rango de frecuencias altas de hasta 20kHz, este seria el equivalente a una frecuencia de muestreo de 44kHz al momento de producir una grabacion, al aumentar la calidad a 48khz esta capacidad de filtrar frecuencias altas se expande, es decir que ya no serian 20khz que usa el oido, sino serian 25khz (solo es un ejemplo).
si habrás escuchado del FFT, es una versión optimizada de este teorema, ya que tiene su aplicación mayormente en los analizadores de espectro, tanto en ecualizadores, como en un analizador digital o espectrograma. el FFT, nos permite obtener la capacidad de analizar una muestra en un rango simplificado de 20Hz a 20kHz, aun cuando se trabaja a altas frecuencias de muestreo por ejemplo 96Khz, el FFT lo simplifica a el rango de 20hz -20khz, siendo este una herramienta fundamental para analizar nuestra música.

#6
Es lo que decía yo, es como raro saber perfectamente el teorema y no saber sus aplicaciones, o por ultimo deducirlas.

#12
Ojo que la gente se confunde, una cosa es el teorema y otra toda la matemática asociada a su aplicación. En estricto rigor el teorema se aplica en todo lo que refiera a procesamiento de señales, ya que establece la base para cualquier análisis, el hecho de que toda señal es una suma de señales sinusoidales.
Las transformadas no son el teorema, si no su aplicación, es la aplicación matemática de lo que declara el teorema.