Creo que te lo estás tomando como algo personal, y no deberías.
Te diré que FFT's, a mano, no he hecho muchas. CTFT's y DTFT's e incluso convoluciones sí he hecho unas cuantas. También he visto a mucha gente hacerlo siguiendo el "método" sin entender muy bien lo que estaban haciendo. Aunque no me parece relevante para esta discusión.
También creo que mi anterior post expresa bastante claramente cómo defino cada uno de los conceptos, pero respeto que si te quieres llevar el Scattergories porque crees que no estoy tu altura intelectual (aunque no me conozcas de nada y no tengas ni idea de mi vida académica o profesional) estás en tu derecho.
Y también te diré que esto, definitivamente, se ha vuelto una batalla dialéctica. Llamar "fase instantánea" a la "fase" o llamar "fase" al "desplazamiento de fase" no determina para nada la comprensión de un concepto. Simplemente es poner nombres diferentes a dichos conceptos. En tu último post no paras de repetir que confundo conceptos y explicar exactamente lo que yo ya he expuesto basándote en que cuando yo escribo fase tú lees fase inicial, lo que, evidentemente, mezcla los conceptos.
Por ejemplo:
dli escribió:
A es efectivamente la amplitud, y es un parámetro que define la onda. El valor máximo de la función no puede ser mayor que la amplitud, pero eso es distinto a lo que tu estás diciendo, porque el valor de la función en un instante determinado, sí puede ser distinto de la amplitud.
No, eso no es distinto a lo que yo estoy diciendo. Yo estoy diciendo que el valor de la función varía en función del tiempo, y, puesto que dicho valor sólo puede oscilar entre A*1 y A*(-1), A representa el valor máximo de la función.
dli escribió:
Vaya una forma de marear al personal. No mezcles senos y cosenos porque no conduce a ningún sitio. Es obviamente una señal con fase 0, bastante habitual por otra parte. Y lo que me indica esta pregunta es que efectivamente, no has hecho nunca una FFT, matemáticamente me refiero.
La pregunta no implica nada, ya que no la estoy respondiendo. Precisamente ese es el objeto de hacer la pregunta: evaluar la respuesta. Donde tú dices es una señal con fase 0, yo digo es una señal con fase inicial 0, o con desplazamiento de fase 0. Significa lo mismo, pero siempre se puede utilizar la dialéctica para crear "un error de concepto". En cuanto a tus elucubraciones de lo que he hecho o dejado de hacer, mejor no entrar.
dli escribió:
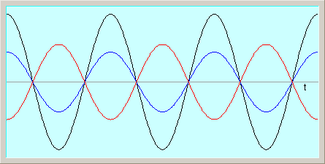
Bonito dibujo. Yo creo que ya he contestado varias veces a esa pregunta... si no se está quieta, ¿para que la quieres?... ¿cómo analizas la suma de dos señales en función de su fase si no sabes que fase tienen porque está cambiando todo el tiempo?
Porque, si tienen la misma frecuencia, ambas varían en función del tiempo EXACTAMENTE A LA VEZ. Claro, que eso ya lo explicaba en el post. Y sí, el gráfico es muy bonito, además de tremendamente útil.
dli escribió:
El cacao aquí ya se empieza a hacer importante, porque estás mezclando conceptos. Estás diciendo que como la fase en el dominio del tiempo sí cambia (porque tu dices que la fase cambia todo el rato), al pasar al dominio de la frecuencia, también varía, pero en función de la frecuencia... tremenda empanada mental. Vamos a ver si consigo deshacerla, o por lo menos, aunque te enfades mucho conmigo y no des el brazo a torcer, a ver si hago que te pique la curiosidad y la vas deshaciendo poco a poco:
Cuando lees mi frase "Si nuestra señal sólo tiene un componente frecuencial, lógicamente no podemos representar su fase en función de la frecuencia ya que sólo tiene valor para 1 frecuencia.", en caso de que no la hayas citado sin ni siquiera leerla, ¿Qué has entendido exactamente?. Si una señal, como el ruido rosa, tiene componentes frecuenciales por todo el espectro, al representar dicha señal en el dominio de la frecuencia, veremos que los valores de magnitud y "fase" (lo que yo llamo fase inicial) varían en función de la frecuencia. No veo que sea tan difícil de entender lo que quiero decir. Claro que una señal que consiste en una onda senoidal no va a tener una representación en el dominio de la frecuencia que varíe con la frecuencia. Igual que el valor de la función en un instante de tiempo determinado no va a variar en función del tiempo.
Voy a reescribir mi exposición, pero esta vez estableciendo el significado de cada uno de los términos antes de usarlos y usándolos con sumo cuidado después. ¿Leísteis el enlace al texto de Cortázar? Creo que esto empieza a parecerse más de lo que yo esperaba.
De la entrada en inglés de la wikipedia:
Alguien escribió:
Phase in sinusoidal functions or in waves has two different, but closely related, meanings. One is the initial angle of a sinusoidal function at its origin and is sometimes called phase offset. Another usage is the fraction of the wave cycle which has elapsed relative to the origin.
La segunda definición, a la que, por cierto, no añade apellido como a la primera, me voy a permitir traducirla: "La fracción del ciclo de la onda que ha transcurrido relativa al origen"
Si te sientes más cómodo añadiendo el apellido a la segunda definición, a partir de ahora voy a establecer los términos como siguen:
Fase: Ángulo inicial de una función senoidal en su orígen. Aunque en la wikipedia no lo pone cuando habla de orígen se refiere al orígen en el tiempo o t = 0. Ahora veremos esto.
Fase Instantánea: La fracción del ciclo de la onda que ha transcurrido relativa al origen (traducción literal, aunque siempre se me puede acusar de no saber inglés).
Si quedamos en que la wikipedia en inglés es aceptable como fuente de información, me voy a permitir, además citar esta otra entrada:
http://en.wikipedia.org/wiki/Amplitude
Alguien escribió:
The amplitude of a periodic variable is a measure of its change over a single period (such as time or spatial period).
[...]
In audio system measurements, telecommunications and other areas where the measurand is a signal that swings above and below a zero value but is not sinusoidal, peak amplitude is often used. This is the maximum absolute value of the signal.
Me tomo la libertad de traducir otra vez:
"La amplitud de una variable periódica es una medida de su variación durante un único periodo (como pueden ser un periodo de tiempo o de espacio).
En medición de sistemas de audio, telecomunicaciones u otras áreas donde el objeto de la medición es una señal que oscila por encima y por debajo de un valor cero pero no es senoidal, la amplitud de pico es usada con frecuencia. Éste es el valor máximo absoluto de la señal."
Como queremos dar una definición de los términos antes de emplearlos,
Amplitud : Valor máximo de la señal. Lo que la wikipedia en inglés define como amplitud de pico.
Amplitud instantánea: Valor de la señal en un instante determinado. Determinado, obviamente, por la variable de tiempo t. Ahora veremos esto. Como sé que no te gusta esta acepción de la palabra amplitud, en lo sucesivo utilizaré el sinónimo
Valor de la función.
Volvamos a la función que describe el comportamiento de nuestra señal senoidal.
Y(t) = A*cos(w*t + Phi)
donde
Y(t) es el
Valor de la función con respecto al tiempo. Nótese el uso de Y en lugar de X ya que, en las representaciones gráficas en el dominio del tiempo dicho valor se situará en el eje vertical, normalmente eje Y o eje de ordenaddas. En el eje horizontal colocaremos la variable t, que es la única variable necesaria para evaluar dicha función.
A es el parámetro antes definido como
Amplitud. Puesto que la función seno a la que multiplica sólo puede oscilar entre los valores 1 y -1, podemos deducir que el
Valor de la función oscilará entre
Amplitud y
-Amplitud.
w es el parámetro Frecuencia Angular y viene determinado por 2*pi*f, siendo f la frecuencia de la oscilación. Se mide en radianes y su equivalencia con los grados es pi = 180º, es decir 2*pi = 360º. 2*pi ó 360º es lo que consideramos un periodo o ciclo, que es el patrón que se repite en nuestra señal periódica.
Phi es lo que hemos definido como
Fase
El argumento de la función coseno w*t + Phi es lo que hemos definido como
Fase Instantánea. Al contener la variable t el valor de esta expresión depende del tiempo, o varía a lo largo del tiempo, al igual que el
Valor de la función.
La variable t (tiempo) es imprescindible para entender nuestra función.

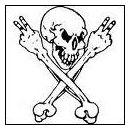
En la gráfica vemos nuestra función representada en los ejes de coordenadas. El eje X representa la variable tiempo y está rotulada con los valores de
Fase instantánea para el periodo de nuestra función. Si queremos saber cómo se correlacionan dichos valores, tenemos que evaluar la función de la
Fase instantánea a la que podemos llamar Fase(t) y que, como ya hemos visto se define como
Fase(t) = w*t + Phi
Así si nuestra frecuencia es 100Hz, el valor pi en nuestro eje X representa, para la función coseno (en azul discontinuo), sabiendo que en dicho gráfico el valor de Phi es 0 (la función seno para t = 0, es decir para Fase(0) = 0 , por tanto, cos(0) = 1. Vemos que en el gráfico para t = 0 el valor en el eje Y es 1. Esto nos indica que esta señal no está desplazada con respecto al origen, o, como hemos definido la
Fase, el ángulo inicial en su origen es 0)
pi = 2*pi*100*t + 0 => t = pi/(2*pi*100) => t = 1/200 => t = 0.005 s ó 5 ms
El tiempo no se acaba al final de nuestro periodo, sino que se vuelve a repetir. Así cuando llegamos a 2*pi en un ciclo, nos encontramos en 0 en el siguiente ciclo, y los valores se vuelven a repetir.
Como para nuestra señal de 100Hz en la
Fase instantánea pi el tiempo que ha transcurrido en el primer ciclo es 5ms, lógicamente para la
Fase instantánea 2*PI el tiempo transcurrido será 10ms. Esto se corresponde con 1s / 100Hz = 0.01 segundos por ciclo. Como nuestra señal se repite en el tiempo, sólo necesitamos saber en qué parte del ciclo o
Fase instantánea se encuentra para saber el valor que tendremos en nuestro eje Y. Así, en t = 15 ms, sabemos que estamos en
Fase instantánea pi y nuestro valor en el eje Y será -1.
¿Y a nosotros qué nos importa todo esto si nos vale con saber el número mágico del parámetro Phi (o
Fase) para hacer nuestros cálculos?
Nos importa porque ese número significa algo. Significa exactamente en qué parte del ciclo empieza nuestro ciclo. Pero para entender qué significa ésto tenemos que entender lo que pasa en un ciclo a lo largo del tiempo, porque eso es lo que ocurre en realidad con nuestra señal.
Tener un valor determinado de Phi (o
Fase) nos indica dónde comienza nuestra señal para t = 0. Esto implica que para cualquier t nuestra señal estará desplazada en el eje X en la misma proporción.
Si volvemos a nuestro gráfico, y a nuestra señal, y en lugar de tomar Phi como 0 tomamos pi/2 (90º), nuestra señal pasará a posicionarse encima de la roja.
Esto es, Fase(t) = 2*pi*100*t + pi/2 , y, por tanto, Fase(0.005) = 2*pi*100*0.005 + pi/2 => Fase(0.005) = 2*pi*0.5 + pi/2 => Fase(0.005) = 3*pi/2.
Por tanto, cos(3*pi/2) = 0.
Nuestro valor en el eje Y para nuestra señal con valor Phi = pi/2 será 0 para t = 5 ms (tomando nuestra frecuencia como 100 Hz), que coincide con el valor de la señal roja en el gráfico.
Eso es lo que significa el valor de Phi, al que estamos llamando
Fase
¿Por qué es importante conocer este valor para saber cómo interaccionan señales con la misma frecuencia?
Como las señales con la misma frecuencia varían su
Valor de la función a lo largo del tiempo exactamente a la vez, nos basta conocer la diferencia RELATIVA entre sus
Fases instantáneas o sus diferencias de
Fase o, por ponerle un nombre, desfase para saber cuál será el resultado de la interacción. Esto no quiere decir que las señales dejen de oscilar a lo largo del tiempo, sólo quiere decir que nos basta saber que su frecuencia es la misma para poder calcular el resultado de dicha interacción conociendo los parámetros
Amplitud y
Fase de cada una de ellas (lo cual es bastante lógico ya que, como hemos visto, sólo tenemos 3 parámetros en las señales que estamos viendo, y esto implica conocer los 3).
¿Cómo interaccionan dos señales de igual frecuencia y
Amplitud pero de distinta
Fase?
Como comprendemos el significado de la anterior pregunta, podemos intentar encontrar una respuesta.
Si definimos dos señales como X(t) e Y(t), podemos definir su suma como Z(t) = X(t) + Y(t), es decir
Z(t) = A*cos(w*t + Phi1) + A*cos(w*t + Phi2) => Z(t) = A*( cos(w*t + Phi1) + cos(w*t + Phi2) )
Gracias a la siguiente relación trigonométrica sabemos que:
cos(a) + cos(b) = 2* ( cos( (a+b)/2 ) * cos( (a-b)/2 ) )
Por tanto:
Z(t) = 2*A*cos ( (Phi1-Phi2)/2 ) * cos (w*t + (Phi1+Phi2)/2)
Entonces la
Amplitud de la señal resultante será 2*A*cos ( (Phi1-Phi2)/2 ) Si, por ejemplo, el desfase entre las señales es de pi (una tiene Phi1 = 0 y la otra Phi2 = Pi, como el resultado de cos(pi/2) = 0, la
Amplitud será 0 y el
Valor de la función también será 0. Eso son señales cancelándose por tener misma
Amplitud y estar desfasadas 180º. En el gráfico de arriba vemos 2 señales desfasadas pi/2 (90º)
La
Fase Instantánea de la señal resultante será Fase(t) = cos (w*t + (Phi1+Phi2)/2)
y la
Fase de la señal resultante será (Phi1+Phi2)/2
De donde podemos deducir que la señal resultante será una señal de igual frecuencia, cuya
Amplitud depende de las
Fases de las señales que está interaccionando y cuya fase será igual a la mitad de la suma de las
Fases de las señales que estamos sumando.
Como vemos, el tiempo no se ha detenido, pero nosotros nos podemos ahorrar cálculos gracias a las matemáticas por la sencilla razón de que nos basta saber la Fase relativa o desfase entre ambas señales, que no varía con el tiempo. Sin embargo el Valor de la función de las señales sigue oscilando con el tiempo mientras la Fase instantánea sigue recorriendo ciclos.
La
Fase no tiene nada de mágica ni de incomprensible. Lo es si la queremos definir como un parámetro de una función que no significa nada, pero, como estamos viendo, tiene un significado muy concreto.
¿Si la
Fase instantánea no para de moverse por qué en Smaart yo veo la curva de fase quietecita?
Primero tenemos que definir lo que implica ver una señal en el dominio de la frecuencia. hasta ahora heos estado hablando de señales en el dominio del tiempo. Esto quiere decir que nuestra variable t, que significa tiempo, es la variable en
función de la cual se van a definir los valores de nuestras funciones.
Supongamos que hablamos de la función que define la longitud de una circunferencia. L = 2*pi*r donde 2 y pi son valores conocidos (constantes), y r es nuestra variable (el radio de nuestra circunferencia). Cuanto mayor r, mayor será L. Podemos definir L como L(r) = 2*pi*r. Esta función no está en el dominio del tiempo, podríamos decir que está en el "dominio del radio".
Pasa lo mismo con la frecuencia. Nuestras señales en el tiempo se corresponden con señales en el dominio de la frecuencia. Las matemáticas detrás de estas operaciones implican una serie de nociones que, realmente, no vienen al caso. (Esto, obviamente será usado como arma arrojadiza para decir "AlienGroove no tiene ni idea, por eso no lo explica"). En serio, no es una cuestión trivial que sea fácil de exponer en un post. Seguramente tampoco sabría hacerlo bien. Pero sí nos podemos centrar en casos concretos para ver cómo se relaciona esto con nuestro camino hacia la comprensión de "la fase" (nótese que NO uso las negritas aquí).
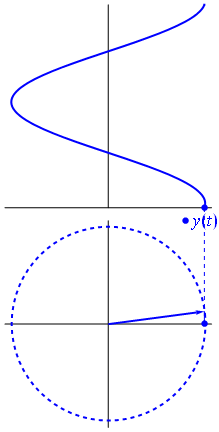
Digamos que cualquier señal periódica se puede descomponer como la suma de señales senoidales. Digamos también que una señal senoidal se puede representar como un número complejo.
Si tenemos que Y(t) = A*cos(w*t + Phi) en el dominio del tiempo, diremos que se corresponde con un número complejo de radio o magnitud A y
Fase o ángulo Phi. Su notación será z = a + bj, donde a será la parte real y b será la parte imaginaria.
La relación entre el número complejo y nuestra señal se puede establecer como:
Phi = arctg(b/a)
A = sqrt(a^2+b^2)
Entonces Z representa nuestra señal para la frecuencia f y frecuencia angular w = 2*pi*f
Estos son los vectores en el plano imaginario que antes sumábamos con la calculadora.
Podemos establecer la relación entre nuestra señal en el tiempo y su Fasor que se expresa como (nos lo vamos a tener que creer)
A*cos(w*t + Phi) <=> A*e^(Phi*j)*e^(j*w)
Si nos fijamos en la expresión de la derecha, podemos establecer w como nuestra variable. Así
Y(w) = A*e^(Phi*j)*e^(j*w)
Que representa nuestra señal en el dominio de la frecuencia. Esto tiene varias implicaciones.
Si ahora representamos en una gráfica nuestra señal, el eje horizontal, como estamos en el dominio de la frecuencia, representará la frecuencia. Vemos que ahora A y Phi dependen de la frecuencia, que es nuestra variable.
Como nuestra señal sólo tiene una frecuencia, sólo tendrá valores para ésa frecuencia en concreto en el dominio de la frecuencia. Eso equivaldría a tener sólo el valor para un instante de tiempo en el dominio del tiempo.
Así si representamos la
Fase Phi en el eje vertical contra la frecuencia (eje horizontal) sólo habría un punto que dibujar para todo el espectro.
Si nuestra señal tuviera más componentes frecuenciales (la fórmula no sería exactamente así) podríamos dibujar más puntos en nuestra gráfica ya que tendríamos valores, tanto de
Amplitud como de
Fase para cada uno de esos componentes. Cuando tenemos componentes para todo el espectro, podremos trazar una curva tanto de magnitud (
Amplitud) como de
Fase
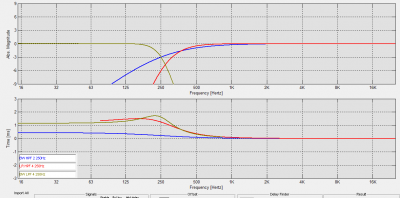
Si tenemos una señal de entrada a un sistema (ruido rosa) cuyas componentes frecuenciales abarcan todo el espectro y una salida cuyas componentes frecuenciales abarcan, también, todo el espectro y hallamos el resultado de la división entre ambas, lo que se llama función de transferencia, tendremos información de magnitud y fase para cada una de las frecuencias en que se divide nuestro espectro.
Esta información de magnitud y de
Fase nos está diciendo la diferencia que existe entre los valores de magnitud y
Fase de entrada y salida para cada una de las frecuencias. Nuestra curva de
Fase nos est'a indicando el desplazamiento de fase o desfase que existe para cada una de las frecuencias. Por eso este valor no varía en el tiempo, porque es RELATIVO. Ya sabemos que Phi (la
Fase) es parámetro, y, lógicamente no varía con el tiempo. Lo que vemos es la relación entre este parámetro de la señal de entrada y el mismo parámetro en la señal de salida. Como la función de transferencia está en el dominio de la frecuencia, ambos parámetros variarán en función de la frecuencia, dando lugar a las curvas de magnitud y de fase.
Todo lo que pone arriba es lo que yo entiendo como "la fase".
Supongo que bastaba con saber que "la fase" es un número que me sirve para saber lo que va a pasar con señales al sumarlas, aunque creo que es productivo realmente entender de qué se trata.
Y si sabes de qué se trata, te dará igual que alguien se refiera a ella como fase inicial, desfase, desplazamiento de fase, fase instantánea, Phi o cualquier otra cosa, sobre todo teniendo en cuenta que para todas esas acepciones la gente suele usar la expresión "la fase".
Hace rato que esto ha perdido ya el sentido y la verdad es que me ha costado escribir este tocho infumable que dudo que nadie sea capaz de leer. En cualquier caso es mi aportación (apòrtación que ya había hecho y que realmente he traducido a los términos que me han dicho que son correctos, aunque yo tenga mis razones para pensar otra cosa).
Con respecto al resto del post del compañero dli, pues sí, así es.
Un saludo.