chicos, existirá algún modulo que permita crear formas de onda a partir de una linea recta deformable con curvas Bezier, y añadir distintas formas de onda para crear una tabla de ondas variables por un Knob (perilla virtual en este caso) seria un Osc alimentado por un emisor de frecuencia virtual formado también por comas flotantes.. ¿?
les parece si lo escribimos ? por que la fuente de mas abajo hay que llevarlo al lenguaje Ruby y luego escribirlo en Synthmaker o FlowStone,
Fuente: (es de lo que sigue a continuación)
http://www.planetclegg.com/projects/WarpingTextToSplines.html
La interpolación lineal (lerp) entre dos valores escalares se define como sigue:
vlerp = v0 + ( v1 - v0 ) * t
De lo cual se puede crear una función lerp entre dos puntos 2D
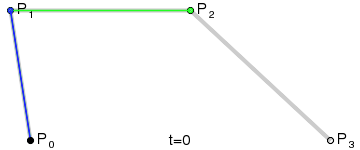
lerp(P0, P1, t) :
xlerp = x0 + ( x1 - x0 ) * t
ylerp = y0 + ( y1 - y0 ) * t
return point (xlerp, ylerp)
La imagen geométrica anterior se puede entonces expresarse como sigue:
P4 = lerp(P0, P1, t);
P5 = lerp(P1, P2, t);
P6 = lerp(P2, P3, t);
P7 = lerp(P4, P5, t);
P8 = lerp(P5, P6, t);
P9 = lerp(P7, P8, t);
Cuando P9 es el punto de la curva para t.
A Bézier cúbica también puede expresarse como un polinomio cúbico con ocho coeficientes: (voy a describir la forma de calcular los coeficientes de los cuatro puntos de control en una fecha posterior)
x = At3 + Bt2 + Ct + D
y = Et3 + Ft2 + Gt + H
Para valores de T entre 0 a 1, estos polinomios producen la coordenadas x e y de un punto en la curva. Los valores fuera de ese rango continúan la función hasta el infinito en algún sitio. La fórmula es realmente lo mismo para las versiones x e y, sólo con diferentes coeficientes. Las ecuaciones se relacionan de forma independiente x e y al valor del parámetro valor de t. Debido a esto las ranuras se pueden extender en tres dimensiones (o más!) Con mucha facilidad.
Entonces, ¿dónde los coeficientes (A.. H) vienen? Para una explicación completa de las cuentas, consulte la sección de recursos en la parte inferior, pero por ahora sólo voy a dar las fórmulas para la conversión de los puntos de control a los coeficientes.
Teniendo en cuenta cuatro puntos de control para la P0 spline .. P3, que tiene valores de (x0, y0) .. (x3, y3), los coeficientes son:
A = x3 - 3 * x2 + 3 * x1 - x0
B = 3 * x2 - 6 * x1 + 3 * x0
C = 3 * x1 - 3 * x0
D = x0
E = y3 - 3 * y2 + 3 * y1 - y0
F = 3 * y2 - 6 * y1 + 3 * y0
G = 3 * y1 - 3 * y0
H = y0
Si fuera necesario para calcular los puntos de control de los coeficientes, aquí están las operaciones inversas:
x0 = D;
x1 = D + C / 3
x2 = D + 2 * C / 3 + B / 3
x3 = D + C + B + A
y0 = H;
y1 = H + G / 3
y2 = H + 2 * G / 3 + F / 3
y3 = H + G + F + E
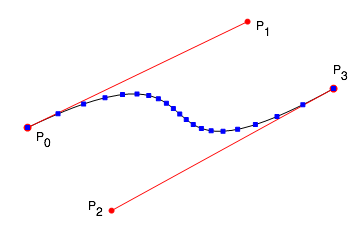
Así que para ilustrar lo que se ha cubierto hasta ahora, he aquí algo de pseudocódigo, utilizando puntos de control P0 .. P3:
/ / Dibujar la Bézier utilizando GDI + función (g es objeto Gráfico)
g.DrawBezier (Pens.Black, P0, P1, P2, P3);
Líneas / / Dibujar conectan los Puntos de Control
g.DrawLine(redPenWithEndCap, P0,P1);
g.DrawLine(redPenWithEndCap, P2,P3);
[[calcular los coeficientes de la A a la H que se describen anteriormente]]
/ / Dibujar 20 puntos, con un incremento fijo para el parámetro t
para (float t = 0; t <= 1; t + = 0.05f)
{
x = At3 + Bt2 + Ct + D
y = Et3 + Ft2 + Gt + H
/ / Función que dibuja una recta lleno en x, coordina y llama.
DrawBoxAtPoint(g, Color.Blue, x, y);
}