Saludos, he estado leyendo, investigando y tratando de comprender el calculo de la absorcion del aire, mas concretamente la pregunta es ¿como funciona el calculador de DoPa relativo a la absorción del aire, por ejemplo? Sabiendo que puedo conseguir y calcular en http://www.doctorproaudio.com/content.php?115-calculadores-proaudio-sonido-dmx sin embargo la intención es comprender como lo hicieron, revisé la ISO 9613-1 que es donde está basada la fórmula pero aún asi no logro dar con los resultados de atenuación que se dan a conocer en db, alguien sabe como hacer el cálculo basado en temperatura(°C), humedad relativa (%)frecuencia (Hz) distancia (metros)? si pueden por favor ejemplifiquen con estos datos de ejemplo : 26°C de temperatura, 45% de humedad relativa, 4000hz como frecuencia y 15 metros de distancia. Estaré muy agradecido de ver el procedimiento, gracias de antemano.
Calculo de absorción del aire ¿como hacerlo?

OFERTAS Ver todas
-
-20%Technics SL-1200M7 Lamborghini
-
-7%Modal Argon8 (B-Stock)
-
-29%Behringer X-Touch Compact

la velocidad de propagación del sonido tiene que ver con los cambios de temperatura y humedad.
la velocidad será mayor cuanto mas denso sea el ambiente en el cual se propaga..evidentemente la humedad y la temperatura afectaran.
se puede calcular la velocidad de propagación del sonido a partir de la humedad y la temperatura, y sus cambios.Si te refieres a eso...si te he entendido bien¿?
Formula para la Variable de Temperatura C, siendo T la temperatura en ºC
C=331,4+ 0,6 T.......puedes hacerlo con C= 343 + 0,6T
siendo C considerado= 343 ms (a 20ºC y 50% Humedad) a veces se puede encontrar cálculos con valores aproximados con 340ms
sabiendo que la FASE es tiempo o distancia....si sabemos que el sonido se propaga mas o menos metros por segundo según los cambios de temperatura.Entonces asumimos que habrá diferencias de tiempo/temporales si cambia C
¿Cuál es el periodo (T) de 4000Hz?
Vamos a usar la formula que relaciona Tiempo(periodo T) y frecuencia (f) concreta
f=4000 Hz ; T=1/ f ; T=0,00025 ms
¿Cuál es la Longitud de Onda ?
Donde la relación de la Longitud de Onda λ (lamda) para esa frecuencia (f) en ese periodo (T) y con esa constante de temperatura (C) es:
λ (lamda)= T x C
λ= 0,00025 x 343
λ=0,08575 metros--LONGITUD DE ONDA de 4000Hz (1 CICLO=1λ)=360º
SI AHORA CAMBIAS EL VALOR DE C, por que varia la temperatura y su humedad....VARIARÁ λ,dandote un valor nuevo....ya podrías comparar, y ver las diferencias de tiempo,distancias,fase que te supone para esa frecuencia 4000Hz.
0,02143 metros ....(1/4λ)=90º UN CUARTO DE LONGITUD DE ONDA de 4000Hz
0,0428 metros ......(1/2λ)=180º MEDIA LONGITUD ONDA de 4000Hz
Hoy en día muchos softwares de gestión de sistemas, te dan la opción,lo recalculan y te muestran las modificaciones para las vías y los procesos automáticamente.

la velocidad será mayor cuanto mas denso sea el ambiente en el cual se propaga..evidentemente la humedad y la temperatura afectaran.
se puede calcular la velocidad de propagación del sonido a partir de la humedad y la temperatura, y sus cambios.Si te refieres a eso...si te he entendido bien¿?
Formula para la Variable de Temperatura C, siendo T la temperatura en ºC
C=331,4+ 0,6 T.......puedes hacerlo con C= 343 + 0,6T
siendo C considerado= 343 ms (a 20ºC y 50% Humedad) a veces se puede encontrar cálculos con valores aproximados con 340ms
sabiendo que la FASE es tiempo o distancia....si sabemos que el sonido se propaga mas o menos metros por segundo según los cambios de temperatura.Entonces asumimos que habrá diferencias de tiempo/temporales si cambia C
¿Cuál es el periodo (T) de 4000Hz?
Vamos a usar la formula que relaciona Tiempo(periodo T) y frecuencia (f) concreta
f=4000 Hz ; T=1/ f ; T=0,00025 ms
¿Cuál es la Longitud de Onda ?
Donde la relación de la Longitud de Onda λ (lamda) para esa frecuencia (f) en ese periodo (T) y con esa constante de temperatura (C) es:
λ (lamda)= T x C
λ= 0,00025 x 343
λ=0,08575 metros--LONGITUD DE ONDA de 4000Hz (1 CICLO=1λ)=360º
SI AHORA CAMBIAS EL VALOR DE C, por que varia la temperatura y su humedad....VARIARÁ λ,dandote un valor nuevo....ya podrías comparar, y ver las diferencias de tiempo,distancias,fase que te supone para esa frecuencia 4000Hz.
0,02143 metros ....(1/4λ)=90º UN CUARTO DE LONGITUD DE ONDA de 4000Hz
0,0428 metros ......(1/2λ)=180º MEDIA LONGITUD ONDA de 4000Hz
Hoy en día muchos softwares de gestión de sistemas, te dan la opción,lo recalculan y te muestran las modificaciones para las vías y los procesos automáticamente.

A todo lo anterior , el calculador utiliza la distancia en su ultimo recuadro....para calcular las diferentes atenuaciones que se dan al aumentar la distancia a la fuente de sonido.
el calculo de antes, lo hemos calculado para un punto de distancia "X"m. 0 m no por que seria encima de la fuente, y eso no puede ser.
Sabiendo el nivel de presión sonora que sigue la relación 1W/1m , sabiendo la sensibilidad el altavoz (ej: 94dB 1w/1M según especificaciones) y la potencia amplificada en W (ej: 1000W) podemos calcular el SPL a 1metro.
Ahora usando la formula del cuadrado de la distancia, sabemos que cada vez que doblamos la distancia del punto "X" a la fuente nuestra energía decrece 6dB, usaremos la ecuación:
atenuación por distancia= 20 Log I/ I ref I=2 metros , el doble de 1m.. I ref: 1 Metro
20Log2- 20Log1
20Log2 - 0
20Log2= 6 dB
Si sabemos el SPL del altavoz con esa temperatura C a 1m(dB=10Log P/Pref...relación de diferencias de potencia Vatios se usa 10Log no 20Log) , con esa distancia "X"...si variamos la distancia por ejemplo 2X...variará el SPL....y su verá atenuado. con hasta un -6dB cada vez que doblemos la distancia.
y así salen los resultados del calculador,en base a esto.el calculador te da menos información de la que yo he realizado a mano. pero te calcula en dB la atenuación ocurrida por distancia mas que por temperatura.Para mi, es incompleto, en ese aspecto ya que no relaciona Potencia, ni sensibilidad del altavoz en el mismo calculador. Solo calcula a partir de que pongas valores a la distancia >0....¿ y si quiero saber lo que varía la fase según los cambios de temperatura para una frecuencia ( 4000Hz) en un punto fijo X de la audiencia, solo por que ha variado la temperatura 10 grados?....sin suponer lo que va a pasar a 2 m, 6m, 8m, 10m de ese punto.que eso vendrá luego...eso el calculador no te lo hace ( pero el que esta justo encima de el , el de longitud de onda sí)...primero lo tienes que sacar tu y luego calcular las distancias y sus correspondientes atenuaciones, en eso si es útil.
el calculo de antes, lo hemos calculado para un punto de distancia "X"m. 0 m no por que seria encima de la fuente, y eso no puede ser.
Sabiendo el nivel de presión sonora que sigue la relación 1W/1m , sabiendo la sensibilidad el altavoz (ej: 94dB 1w/1M según especificaciones) y la potencia amplificada en W (ej: 1000W) podemos calcular el SPL a 1metro.
Ahora usando la formula del cuadrado de la distancia, sabemos que cada vez que doblamos la distancia del punto "X" a la fuente nuestra energía decrece 6dB, usaremos la ecuación:
atenuación por distancia= 20 Log I/ I ref I=2 metros , el doble de 1m.. I ref: 1 Metro
20Log2- 20Log1
20Log2 - 0
20Log2= 6 dB
Si sabemos el SPL del altavoz con esa temperatura C a 1m(dB=10Log P/Pref...relación de diferencias de potencia Vatios se usa 10Log no 20Log) , con esa distancia "X"...si variamos la distancia por ejemplo 2X...variará el SPL....y su verá atenuado. con hasta un -6dB cada vez que doblemos la distancia.
y así salen los resultados del calculador,en base a esto.el calculador te da menos información de la que yo he realizado a mano. pero te calcula en dB la atenuación ocurrida por distancia mas que por temperatura.Para mi, es incompleto, en ese aspecto ya que no relaciona Potencia, ni sensibilidad del altavoz en el mismo calculador. Solo calcula a partir de que pongas valores a la distancia >0....¿ y si quiero saber lo que varía la fase según los cambios de temperatura para una frecuencia ( 4000Hz) en un punto fijo X de la audiencia, solo por que ha variado la temperatura 10 grados?....sin suponer lo que va a pasar a 2 m, 6m, 8m, 10m de ese punto.que eso vendrá luego...eso el calculador no te lo hace ( pero el que esta justo encima de el , el de longitud de onda sí)...primero lo tienes que sacar tu y luego calcular las distancias y sus correspondientes atenuaciones, en eso si es útil.

#3 excelente es una respuesta por demás completa y muy muy paciente, gracias por tomar el tiempo de redactarla, ahora quiero revisar un poco más


CLP escribió:acá si bien es muy cierto sigo sin ver la relación (humedad-temperatura) ya que estamos tomando como referencia que ya es 50% de humedad, y aun asi la humedad relativa es una variable que afecta el resultado, ¿como lo hace? ya se como varía la velocidad del sonido por temperatura pero no como lo afecta la humedad relativa, por demás absolutamente clara y completa la respuesta, si me ayudas en este punto estaré aún más agradecido CLP.Formula para la Variable de Temperatura C, siendo T la temperatura en ºC
C=331,4+ 0,6 T.......puedes hacerlo con C= 343 + 0,6T
siendo C considerado= 343 ms (a 20ºC y 50% Humedad) a veces se puede encontrar cálculos con valores aproximados con 340ms




Si es facilísimo...
Sengpielaudio
● Formula for calculating the damping of air ●
Damping of Air of High Frequencies (Dissipation)
ISO 9613-1:1993 − Acoustics − Noise Absorption by Air − Attenuation of sound during propagation outdoors − Calculation of the absorption of sound by the atmosphere.
Attenuation due to atmospheric absorption is specified as a function of the frequency of the sound from 50 Hz to 10 kHz and that is really no ultrasound.
There are 4 parameters for calculating air damping:
1) Frequency f in Hz.
2) Temperature T in K (Kelvin). Can be fixed to a standard room temperature of 293.15 K
= 20°C = 68°F.
3) Relative Humidity h in %. Can be fixed to a standard of 50 to 60% or whatever represents a standard RH for one's circumstances.
4) Atmospheric pressure p in kPa (kilopascal). Can be fixed to a standard of 101.325 kPa (standard pressure at sea level).
as = a · s [dB] total absorption at distance s
pt = pi · exp(−x · as) [Pa]
x = 1 / (10 · log ((exp(1))2) = ca. 0.1151
Delta Lt = 20 · log (pi / pt) = as [dB]
a = 8.686 · f2 · ((1.84 · 10−11 · (pa / pr)−1 · (T / To)1/2) + y) [dB/m]
y = (T / To)−5/2· (0.01275 · exp (−2239.1 / T) · (frO + f2 / frO)−1 + z)
z = 0.1068 · exp (−3352 / T) · (frN + f2 / frN)−1
frO = (pa / pr) · (24 + 4.04 · 104 · h · ((0.02 + h) / (0.391 + h)))
frN = (pa / pr) · (T / To)−1/2 · (9 + 280 · h · exp (−4.170 · ((T / To)−1/3−1)))
h = hr · ((psat / pr) / (pa / pr)) = hr · (psat / pa)
psat = pr · 10(−6.8346 · (To1 / T)^1.261 + 4.6151)
a ........ pure-tone sound attenuation coefficient, in dB/m, for atmospheric absorption
s ........ distance in m through which the sounds propagates
pi ....... initial sound pressure amplitude in Pa
pt ....... sound pressure amplitude in Pa
pa ...... ambient atmospheric pressure in kPa
pr ....... reference ambient atmospheric pressure: 101.325 kPa
psat ... saturation vapor pressure equals:
................ International Meteorological Tables WMO-No.188 TP94
................ World Meteorological Organization - Geneva Switzerland
T ........ ambient atmospheric temperature in K (Kelvin).
........... K = 273.15 + Temperature in °C (Celsius)
To ...... reference temperature in K: 293.15 K (20°C)
To1..... triple-point isotherm temp: 273.16 K = 273.15 + 0.01 K (0.01°C)
h ........ molar concentration of water vapor, as a percentage
hr........ relative humidity as a percentage
f ......... frequency
frO ..... oxygen relaxation frequency
frN ..... nitrogen relaxation frequency
x ........ a help factor to shorten formula − improvement by E. Desart
y ........ a help factor to shorten formula
z ........ a help factor to shorten formula
Sengpielaudio
● Formula for calculating the damping of air ●
Damping of Air of High Frequencies (Dissipation)
ISO 9613-1:1993 − Acoustics − Noise Absorption by Air − Attenuation of sound during propagation outdoors − Calculation of the absorption of sound by the atmosphere.
Attenuation due to atmospheric absorption is specified as a function of the frequency of the sound from 50 Hz to 10 kHz and that is really no ultrasound.
There are 4 parameters for calculating air damping:
1) Frequency f in Hz.
2) Temperature T in K (Kelvin). Can be fixed to a standard room temperature of 293.15 K
= 20°C = 68°F.
3) Relative Humidity h in %. Can be fixed to a standard of 50 to 60% or whatever represents a standard RH for one's circumstances.
4) Atmospheric pressure p in kPa (kilopascal). Can be fixed to a standard of 101.325 kPa (standard pressure at sea level).
as = a · s [dB] total absorption at distance s
pt = pi · exp(−x · as) [Pa]
x = 1 / (10 · log ((exp(1))2) = ca. 0.1151
Delta Lt = 20 · log (pi / pt) = as [dB]
a = 8.686 · f2 · ((1.84 · 10−11 · (pa / pr)−1 · (T / To)1/2) + y) [dB/m]
y = (T / To)−5/2· (0.01275 · exp (−2239.1 / T) · (frO + f2 / frO)−1 + z)
z = 0.1068 · exp (−3352 / T) · (frN + f2 / frN)−1
frO = (pa / pr) · (24 + 4.04 · 104 · h · ((0.02 + h) / (0.391 + h)))
frN = (pa / pr) · (T / To)−1/2 · (9 + 280 · h · exp (−4.170 · ((T / To)−1/3−1)))
h = hr · ((psat / pr) / (pa / pr)) = hr · (psat / pa)
psat = pr · 10(−6.8346 · (To1 / T)^1.261 + 4.6151)
a ........ pure-tone sound attenuation coefficient, in dB/m, for atmospheric absorption
s ........ distance in m through which the sounds propagates
pi ....... initial sound pressure amplitude in Pa
pt ....... sound pressure amplitude in Pa
pa ...... ambient atmospheric pressure in kPa
pr ....... reference ambient atmospheric pressure: 101.325 kPa
psat ... saturation vapor pressure equals:
................ International Meteorological Tables WMO-No.188 TP94
................ World Meteorological Organization - Geneva Switzerland
T ........ ambient atmospheric temperature in K (Kelvin).
........... K = 273.15 + Temperature in °C (Celsius)
To ...... reference temperature in K: 293.15 K (20°C)
To1..... triple-point isotherm temp: 273.16 K = 273.15 + 0.01 K (0.01°C)
h ........ molar concentration of water vapor, as a percentage
hr........ relative humidity as a percentage
f ......... frequency
frO ..... oxygen relaxation frequency
frN ..... nitrogen relaxation frequency
x ........ a help factor to shorten formula − improvement by E. Desart
y ........ a help factor to shorten formula
z ........ a help factor to shorten formula

Genial #7 Saludos Manelfunk, ahora lo puedes ejemplificar? con estos datos como ejercicio
1) Frecuencia 4000hz
2) temperatura en K :298,15
3:Humedad relativa de 30%
4: Presion atmosferica estandar 101.325 kPa
Muchas gracias de antemano!
1) Frecuencia 4000hz
2) temperatura en K :298,15
3:Humedad relativa de 30%
4: Presion atmosferica estandar 101.325 kPa
Manelfunk escribió:
There are 4 parameters for calculating air damping:
1) Frequency f in Hz.
2) Temperature T in K (Kelvin). Can be fixed to a standard room temperature of 293.15 K
= 20°C = 68°F.
3) Relative Humidity h in %. Can be fixed to a standard of 50 to 60% or whatever represents a standard RH for one's circumstances.
4) Atmospheric pressure p in kPa (kilopascal). Can be fixed to a standard of 101.325 kPa (standard pressure at sea level).
Muchas gracias de antemano!


ahora se entiende por que estos ajustes aun siendo mas importante la temperatura que la humedad...los hace un ordenador. y nosotros cotejamos los datos, los comparamos, los analizamos, los estudiamos, los estrapolamos, los relacionamos...y los volvemos a meter en el ordenador/app calculador para ver las variaciones

#9 vale! solo lo solicité porque creo que la mejor manera de verlo es un ejemplo! pero no hay problemas, gracias.
Es cierto #10 , de hecho mi idea es terminar una hoja de excel que estoy haciendo para mostrar el procedimiento y hacer los calculos.
CLP escribió:ahora se entiende por que estos ajustes aun siendo mas importante la temperatura que la humedad...los hace un ordenador.
Es cierto #10 , de hecho mi idea es terminar una hoja de excel que estoy haciendo para mostrar el procedimiento y hacer los calculos.

Saludos, Siempre hay quien aún lo pueda necesitar así que aqui lo traigo

Lo haré con los datos que ejemplifiqué arriba es decir
1) Temperatura en °K = 298,15°
2) La frecuencia es 4000 Hz
3) Humedad relativa de 30%
4) Presión atmosférica = 101.325
5) Distancia 15 mts
Bien, En primer lugar debemos traducir la temperatura en Función de la presión asi:

Luego la relación con la humedad

Como ya sabemos que la humedad es del 30% entonces:

Obtenemos FrO

Y ahora obtenemos FrN

Ahora Delta (recordando que estamos tomando como referencia 4000 Hz

La relación con la humedad-dB Spl sería simplemente

En este punto ya la atenuación está expresada en dB Spl es decir son 3.911 dB Spl y lo podemos restar a la distancia que son 15 mts

En un redondeo eso sería 0,6 dB Spl, Saludos!!!

Lo haré con los datos que ejemplifiqué arriba es decir
1) Temperatura en °K = 298,15°
2) La frecuencia es 4000 Hz
3) Humedad relativa de 30%
4) Presión atmosférica = 101.325
5) Distancia 15 mts
Bien, En primer lugar debemos traducir la temperatura en Función de la presión asi:
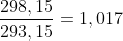
Luego la relación con la humedad
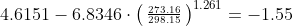
Como ya sabemos que la humedad es del 30% entonces:
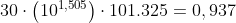
Obtenemos FrO
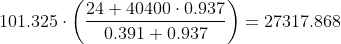
Y ahora obtenemos FrN
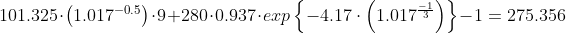
Ahora Delta (recordando que estamos tomando como referencia 4000 Hz

La relación con la humedad-dB Spl sería simplemente
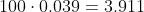
En este punto ya la atenuación está expresada en dB Spl es decir son 3.911 dB Spl y lo podemos restar a la distancia que son 15 mts
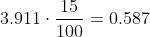
En un redondeo eso sería 0,6 dB Spl, Saludos!!!
Hilos similares
Nuevo post
Regístrate o identifícate para poder postear en este hilo





