elaprendizhispasonic escribió:
¿Tener tanto rango dinamico es bueno o malo? a por cierto he analizado varias veces y en diferentes herramientas para Saber si era una mala lectura
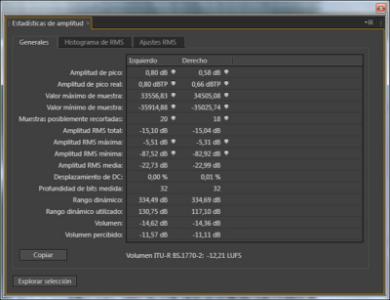
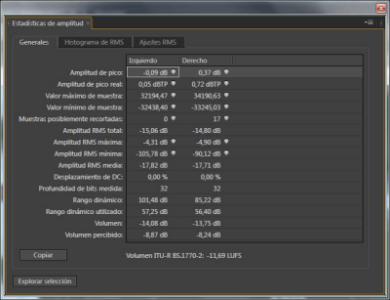
El "Valor máximo/mínimo de muestra" de la primera captura equivale a unos 90 dB, que sería razonable. Pero no veo de dónde salen "Rango dinámico" y "Rango dinámico utilizado", habría que consultar las fórmulas de ese software. Quizá tenga relación con el escalado/conversión entre 24 bit entero y 32 bit flotante.
euridia escribió:
Veo además que los valores máximos de muestra te los da con centésimas. Y ahí ya, me pierdo por completo..... ¿en centésimas?


Las estadísticas de ese software están en base decimal (sea con valores lineales o logarítmicos), pero el audio está en base binaria (formato binary32 del estándar IEEE754). La conversión entre bases hace que no salgan valores "redondos", pero el exponente y mantisa se almacenan como enteros.
En este caso no importa mucho, pero en ciertos cálculos científicos y otros casos sí. Por ello se han creado los formatos decimal32/64/128 en la última versión del IEEE754; otra cosa es que exista hardware y software que lo implemente.
Daniel Lazarus escribió:
Pues sí, rebuscando por ahí he encontrado voces que apuntan a un máximo de +770dB y un mínimo de -897dB, aunque no sé exactamente por qué, parece que se debe a un tema de implementación o yo que sé...

Porque para audio no se usan los números desnormalizados (los que están entre 0 y los normalizados) ya que degradan bastante el rendimiento, incluso cuando están acelerados por hardware.
https://en.wikipedia.org/wiki/Subnormal_number#Performance_issues
Teniendo en cuenta que los normalizados son convenientes por espaciarse logarítmicamente, y ya superan sobradamente los límites de la audición humana: van de -758,6 dB a 770,6 dB.
https://en.wikipedia.org/wiki/Normal_number_%28computing%29
euridia escribió:
El problema que yo he encontrado es que todas las calculadoras entienden que 10^-127 es cero.... y entonces dan error...
La calculadora misma de Windows sirve. Si no, busca una calculadora de precisión arbitraria, en la que puedes aumentarla con el único límite de que te quepa el cálculo en memoria RAM; en Unix, GNU bc y dc son típicas.
----------
Si queréis aprender más de audio digital sin llegar al nivel de programación DSP, os recomiendo la herramienta SoX y leer su buen manual.
http://sox.sourceforge.net/sox.html
Es un procesador lineal de audio en el que vas concatenando efectos con sus parámetros a continuación. Esto es fundamental para entender su sintaxis. La potencia está en su interfaz CLI, que permite automatizarlo con scripting.
Usa enteros con signo de 64 bits para el cálculo interno, así que desaparece la complejidad de IEEE754 (que ni siquiera muchos programadores dominan).
Los efectos estadísticos stat y stats tienen una salida parecida a la captura de pantalla de este hilo. Y la fórmula de cada valor está documentada en el manual. Para evitar redondeo en base decimal, se pueden pasar las opciones -b bits o -s scale.
El efecto synth es bueno para generar tonos de prueba y para afinar por batimiento.
El efecto spectrogram + shell scripting es genial para comparativas visuales. La automatización permite tratar decenas o cientos de combinaciones de parámetros (anidando bucles) que nunca podrían abarcarse a mano. Y con las conclusiones mejoras decisiones futuras.
Ejemplos reales: comparar algoritmos de dithering, investigar a fondo el codec MP3 LAME, comparar formato MP3 vs Vorbis, arreglar una grabación con frecuencia de muestreo no estándar (culpa de un driver de MacOSX) calculando su ratio compensatorio, calcular TruePeak de temas de un álbum por lotes y reducir ganancia si sobrepasa 0 dBFS (para 24 b).
Un saludo.
 *al parecer es una mala lectura
*al parecer es una mala lectura