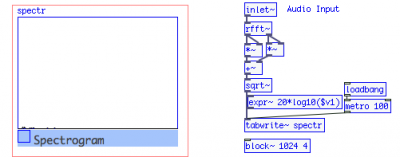
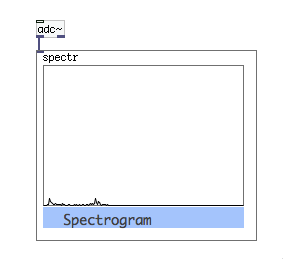
Nox escribió:
Por cierto, lo de la convolución es algo que me ha intrigado siempre. A lo mejor es que no termino de entender el concepto, pero no le veo la utilidad práctica
Es dificil explicarlo, ya que intuitivamente no es nada facil entender una convolucion. Y no te digo ya nada de un (transformador de Hilbert).
Lo importante es que quien lo explique sea alguin didactico (aqui el rey es este
https://ccrma.stanford.edu/~jos/, y sus libros de compra y lectura obligada, eso si, se requiere base matematica)
Pero aqui un breve pincelada (con errores pero que puede permitir entender el asunto):
Existe una relacion matematica entre un espectro temporal (la muestra de audio en el tiempo) y un espectro frecuencial (la informacion frecuencial que corresponde a esa muestra temporal).
Se pasa de una a otra mediante el uso de la Transformada de Fourier Directa (obtienes el espectro frecuencial de una señal de audio a partir de la misma) o Transformada de Fourier Inversa (obtienes una señal de audio a partir de su espectro frecuencial).
Es decir, existe una relacion matematica entre una señal en el tiempo y la misma señal en la frecuencia (si la señal tiene n muestras temporales, via Fourier obtendremos su "vista frecuencial" con n muestras frecuenciales, esto no deja de ser simplemente a nivel matematico un cambio del sistema de coordenadas de referencia en un espacio vectorial de N dimensiones) .
Aqui viene la parte chunga respecto a lo que es una convolucion:
Una operacion de multiplicacion en un espacio de referencia temporal se convierte en una operacion de convolucion en un espacio de referencia frecuencial.
Y a la inversa, una convolucion en un espacio de referencia temporal se convierte en una multiplicacion en un espacio de referencia frecuencial.
Segun la complejidad de la computacion a realizar, se prefiere utilizar un camino o el otro (multiplicar espectros frecuenciales para aplicar filtros o aplicar convolucion a señales temporales para reverbs, etc, etc).
Otro ejemplo, una modulacion en frecuencia (producto de señales temporales) puede resolverse como convolucion en el dominio espectral (expansion en funciones de Bessel y demas ladrillos).
... ¿quieres saber cómo manipularlos en el lenguaje que estés usando, o algoritmos de efectos para pasarlos al lenguaje que estés usando...? Y por cierto, ¿qué lenguaje estás usando, sabes usar ese lenguaje? Es que como dices que tienes una "infraestructura" montada, supongo que será alguna librería, SDK o similar de algún lenguaje que admita android ¿no? 
