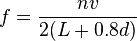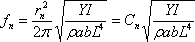Realmente tampoco se hace así,al menos no de forma explícita.Para el cálculo de la longitud de onda necesitas saber la velocidad de propagación de la onda,y esa va a depender del tipo de material,densidad,temperatura,etc...
Yo he planteado lo anterior desde la premisa de que el sonido se iba a generar golpeando el tubo para hacerlo vibrar a su frecuencia natural y no haciendo vibrar el aire de su interior, y para todo lo que expongo ahora sigo dando por hecho que el propósito es ese.
La hipótesis que planteé no es del todo correcta,pero tampoco iba tan desencaminada.
Encontré esta página,que creo que se ajusta más al caso que lo que hemos visto hasta ahora:
http://www.sc.ehu.es/sbweb/fisica/ondas ... _barra.htm
Explica el fenómeno de vibración de una barra elástica,de perfil cuadrangular

Para no perdernos demasiado entre tanto desarrollo,podemos irnos directamente a esto:
 Y
Y: Es el
Módulo de Young, que caracteriza la elasticidad del material.
l: Es el momento de inercia de la sección transversal, que no se exactamente que significado físico tendrá, pero que depende directamente de las dimensiones del perfil ( l = a*b^3 / 12).
rho(esa especie de "p"): Densidad del material.
a: Ancho de la barra.
b: Altura de la barra.
L: Longitud de la barra.
Cn: Modo de vibración.
Para las pruebas que he hecho he usado 2 barras macizas de acero cromado sacadas de impresoras recicladas.
Una de ellas tiene un diámetro de 11 mm y la he cortado en 2 trozos de diferente longitud.La otra barra tiene un diámetro de 8 mm y la he cortado en 3 trozos.
También he usado un travesaño hueco de acero, de perfil cuadrangular (14 mm x 14 mm) de 1 mm de grosor...lo he cortado en 2 trozos.
[ Imagen no disponible ]
Dado que no conozco con exactitud las propiedades del acero del que están hechos estos trastos,no puedo estimar el módulo de Young...y como no tengo con qué pesarlos,pues tampoco puedo calcular la densidad.
Además de esto,tanto en el caso de los travesaños (por no ser macizos) como en el caso de las barras cromadas (por no ser cuadrangulares),no creo que sea demasiado riguroso hacer uso de los parámetros "a" y "b"...Así que simplemente me he dedicado a buscar una constante de proporcionalidad que relacione:
- Por un lado, las frecuencias de resonancia de las dos barras cromadas de 11 mm.
- Por otro lado, las frecuencias de resonancia de las tres barras cromadas de 8 mm.
- Por otro, las frecuencias de resonancia de los 2 travesaños cuadrangulares.
En total, 3 constantes de proporcionalidad (K1, K2 y K3),una para cada tipo de barra.
He cogido la fórmula y he razonado de la siguiente forma,considerando que será aplicable a los 3 casos por separado:
C (modo de vibración) -> Constante
Y (módulo de Young) -> Constante
l (momento inercial) -> Constante
a (anchura) -> Constante
b (altura) -> Constante
rho (densidad) -> Constante
Por lo que ,sacando el término L^4 de la raíz,la fórmula se simplifica,quedando L^2 dividiendo a una constante:
[ Imagen no disponible ]
Hemos obtenido la constante de proporcionalidad "k".
O sea,la frecuencia es inversamente proporcional,no a la longitud de la barra,sino al cuadrado de dicha longitud.
Después de esto,cogí la mayor de las barras cromadas de 11 mm (tiene una longitud de 199 mm), la hice sonar, la grabé y le pasé el analizador de espectro:
[ Imagen no disponible ]
Tiene su fundamental en 3413 Hz.Lo corroboré de oído haciendo sonar una senoidal a esa frecuencia con el generador de tonos del secuenciador (suenan igual,es más,el timbre es casi idéntico).
Tenemos la longitud y la frecuencia...calculamos la constante "k1":
k1 = f * L^2 = 3413 * (0.199)^2 = 135.16
Así que la otra barrita de 11 mm (que tiene una longitud de 167 mm) debería sonar a una frecuencia tal que:
f = k1 / L^2 = 135.16 / (0.167)^2 = 4846.35 Hz
Pues la hice sonar,le pasé el analizador,verifiqué con el generador de tonos... y efectivamente:
[ Imagen no disponible ]
Después hice lo mismo con las barras cromadas de 8 mm.Cogí la mayor (154 mm de longitud),le pasé el analizador y medí una fundamental de 4134 Hz,por lo que la constante k2 es:
k2 = 4134 * (0.154)^2 = 98
- Por lo que la barra mediana (130 mm) debería vibrar a:
f = 98 / (0.13)^2 = 5799 Hz
Al pasar el analizador,medí la fundamental en 5803 Hz.
- La barra pequeña (101 mm) debería vibrar a:
f = 98 / (0.101)^2 = 9607 Hz
Al pasar el analizador,medí la fundamental en 9647 Hz...un error de precisión de un 0.5 % aproximadamente,no está mal.
Hice exactamente lo mismo con los travesaños cuadrangulares...tomé el más grande de la foto (264 mm)lo hice sonar...y resulta que este parecía emitir más de un tono aparente.Usando el generador de tonos de nuendo y el oído identifiqué un tono a unos 1370 Hz y otro a 3596 Hz (dejo el archivo de sonido adjunto para que lo podais oir vosotros mismos).Pasando el analizador de espectro, ambos se ven claramente:
[ Imagen no disponible ]
Hice el cálculo de k3 en base al tono más agudo (3596 Hz):
k3 = 3596 * (0.264)^2 = 250.6
Después tomé otro travesaño más grande (319 mm),ya que el pequeñajo de la foto apenas sonaba.
También se percibían 2 tonos al golpearlo (también dejo el archivo de audio adjunto).Con el oído los localizo en 945 y en 2466 Hz.
En el análisis espectral se ven ambos:
[ Imagen no disponible ]
A ver si la frecuencia (del tono más agudo) cumple la proporcionalidad dada por k3...
k3 = 2466 * (0.319)^2 = 250.9 -> La cumple.
Pero es que resulta que los tonos graves también cumplen proporcionalidad con la longitud,no dada por la misma constante,pero hay proporcionalidad.
Y parece ser que ahí es donde está el significado del parámetro Cn (modo de vibración).Si dividimos k3 entre C2 (9.82) y multiplicamos por C1 (3.56),estaremos pasando del modo 2 al modo 1:
k3 * C1 / C2 = 250.9 * 3.56 / 9.82 = 90.9
Y curiosamente esa proporción es la que cumplen de forma aproximada los tonos graves.
O sea,para el cálculo de los distintos tonos que pueda emitir una barra,se van usando los distintos valores de la constante de modo Cn:
C1: 3.56
C2: 9.82
C3: 19.2
C4: 31.8
etc...
Pos eso.
Dejo los archivos de audio de los dos travesaños cuadrangulares.Los grabé con uno de estos
[url=
https://www.hispasonic.com/fotos/micro-palito/2684[/url]
por lo que llevan algo de ruido de fondo.