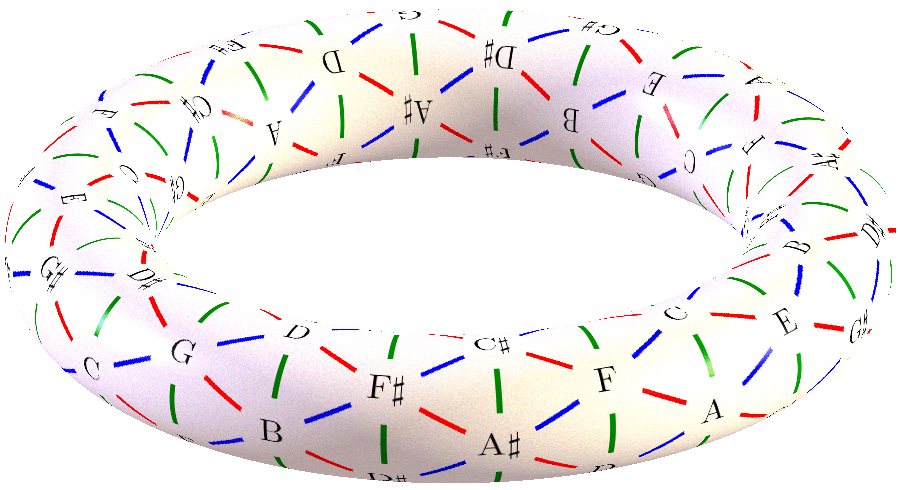
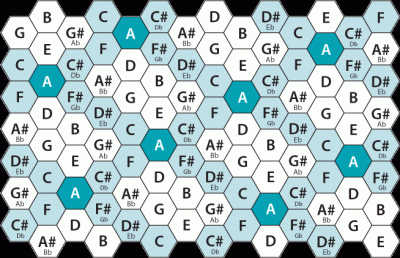
Buenísimo. Este tipo de representaciones son muy interesantes para mostrar la naturaleza cíclica del sistema armónico y esquematizar gráficamente algunas asociaciones, aunque al final el objetivo es siempre llegar a asimilar toda esta información de manera auditiva. También pueden servir como forma de buscar material tonal estimulante para romper un bloqueo.

Bueno, un sistema similar, aunque por terceras menores, es el que usa la acordeón de botones en su mano derecha y que facilita mayor velocidad para la ejecución en comparación con el clásico teclado.
El gráfico que utiliza quintas justas (4 1 5 2 ...) se asemeja a la mano izquierda de los acordeones (el llamado: los bajos)

#4
Ok, lo mejor entonces es que abras un hilo propio para discutir tu invención.

Tienes razón , muchas gracias.
Sólo añadir que hay un instrumento ya hecho con esa forma y se empieza a comercializar. No encuentro el enlace pero lo pondré cuando lo haga.
Un saludo

 mod
mod
#7
Más que opinar del libro, que no he leído, te diré que estas representaciones a mí me resultan útiles, pero sabiendo poner tú el límite de hasta dónde te sirven.
En parte por venir de la ingeniería profunda como formación y por ser de carácter más teorizante que pragmático, estas representaciones que estructuran en formas 'topológicas' las relaciones musicales principales, me han ayudado a entenderlas, memorizarlas y aplicarlas. Pero tampoco hay que obsesionarse con pretender concentrar todo y más en un único objeto como la rueda armónica, tan plagada de líneas que relacionan un montón de cosas (quizá excesivas).
Para mí lo importante es conocer la topología, la distribución (si quieres, los nodos) y conocer (más que representar con tanta profusión) las relaciones que pueden ligarlas. Pero seguro que el libro te permitirá leer mucho, de donde podrás escoger lo que más te sirva a tí.
Aparte de eso, te diría que meterse directamente con una representación de 'toro' (como lo es la rueda: un desarrollo plano de lo que es en esencia un toro) es quizá demasiado fuerte. También estudiamos primero los números naturales, luego los enteros, fraccionarios, reales, complejos... O primero las líneas, luego las superficies y luego los volúmenes.
En ese mismo sentido, los pasos aquí deberían ser primero entender el ciclo de quintas (no deja de ser una línea aunque cerrada sobre sí misma, circular). Y luego acompañas a esa circunferencia otras concéntricas a distancias que sean divisoras de la octava (como tercera menor y tercera mayor), con lo que se completa una representación que como apunta lgarrido es realmente de toro por que se cierra sobre sí misma.
Puedes ver los nodos de la rueda como varios círculos de quintas montados como anillos concéntricos y entre los que hay un desplazamiento de uno a otro por terceras (menores o mayores).
Además por supuesto, ver todo esto con algún sentido musical y no sólo como una mera estructura es también importante.
Ya nos contarás tus impresiones al respecto cuando lo leas.

1
 Baneado
Baneado
Hola Pablo
Lo curioso es que el otro día realizando un encargo de un libro de armonia y otros de historia de música blues y jazz..
me encontré con este esquema que me llamó la atención.
No lo he comprado,pues no estaba dentro de mis tareas pendientes,pero me llamó la atención.
Tienen su propia web y está ahí el vídeo que puso Igarrido
Cuando vi este post,lo relacioné y le di a seguir,hasta que vi la propuesta de Jaime
Yo estoy lejos de poder pensar así..
Como he indicado soy un aprendiz y estudiante.
Lo curioso es que leyéndolos me dio por preguntarles su opinión pues me ha resultado muy amena las criticas vertidas en este hilo y el debate que tienen en el del compañero Jaime,que me pierdo si te soy sincero.
Al postear el link vi que el libro es solamente una página, pueden comprobarlo
Todavia me queda mucho por aprender y tengo que reflexionar mucho si merece la pena pagar 20 euros por eso o ir haciendo a medida que aprendo.
Os agradezco las respuestas.También todo el material de tu web Pablo.Me he salido del debate del hilo de Jaime porque yo no soy pedagogo ni estoy capacitado para pensar tales artilugios.
No tengo tanto camino recorrido ni tanto conocimiento
Un saludo..
Estoy en desacuerdo con lo que se dice en el hilo de Jaime que a un adulto le cuesta más que a un niño a aprender a leer...pero ese no es el tema...quiero aprovechar para decirlo aquí con vuestro permiso,sin ánimo al debate pues no es el tema,pero no estoy de acuerdo con eso que se dice.En mi escuela hay tanto adultos como niños y hay quien aprende y quien abandona
..
Tanto niños con trece años como adultos con cincuenta.
Tenía que soltarlo








 .
.