Hola a todos,
A estas alturas sé que hay ya varios hilos antiguos donde se habla del dither y en los que la teoría queda muy clarita. El caso, es que ayer hice un par de pruebas de exportación y no me queda tan claro que esa teoría sea aplicable en el 100% de los casos. Así que deseo abrir debate entorno a unas capturas de pantalla que paso a compartir.
Por un lado quise ver las diferencias al pasar a distintas frecuencias de muestreo. Mi conclusión es que 44 y 48 KHz son muy semejantes y la diferencia respecto a 96 KHz es abismal. Así pues, siempre que el destino no sea CD (44.1 máximo) o MP3 (48 KHz máximo), un archivo FLAC o MP4 (para Internet) lo dejaría a 96 KHz para guardar la calidad. Esa conclusión va en la línea de un productor de música clásica noruego que lleva un estudio llamado 2L, que afirmaba que en pruebas de doble ciego no es perceptible la conversión de 192 a 96, pero sí de 96 a 48 (lo mismo con 172-88 y 88-44).
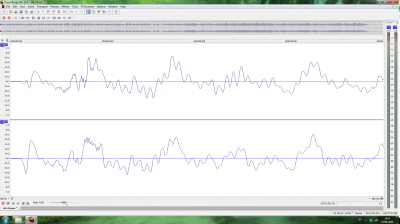
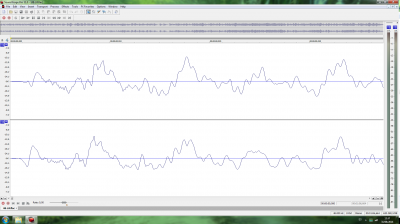
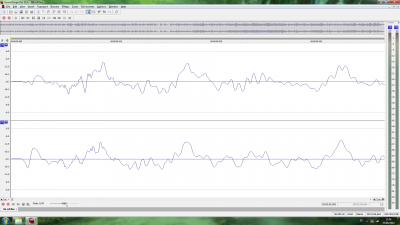
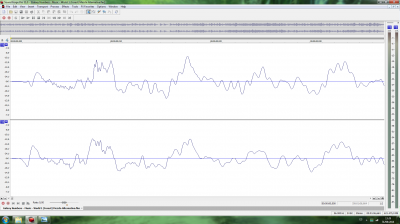
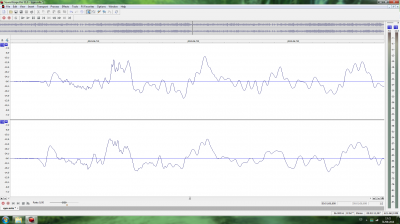
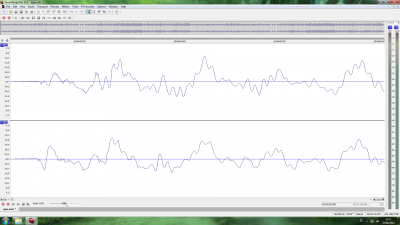
Luego, pasé a ver la diferencia en la onda al introducir o no dither al convertir de 24 bits a 16 bits (conversión obligada tanto para CD como para cualquier archivo de tipo lossy). Supuestamente al hacerlo sin dither, debería producir distorsiones en la onda. Supuestamente, la teoría dice que es preferible el ruido introducido por el dither que esas supuestas distorsiones. El caso es que en la captura de pantalla que corresponde a la conversión sin dither no aprecio diferencias evidentes respecto al original, mientras que la captura de pantalla que corresponde a la conversión con dither se aprecia con perfecta claridad el ruido introducido en la onda. Hay que decir que solo cambié la tasa de bits, no la frecuencia de muestreo. Mi conclusión es que (al menos en este caso) no es buena idea usar dither.
Pregunto, ¿Puede ser porque al no haber material sonoro importante a menos de 96 dB, al pasar de los 140 dB de rango dinámico a los 96, no se produzca ninguna distorsión perceptible, haciendo injustificable el ruido introducido por el dither (que sí es levemente perceptible al oído)? Y en caso de ser eso, acaso hay algún tipo de música que use de forma efectiva ese enorme rango dinámico? Porque yo creo que ni la música clásica lo tiene. Supongo que habrá a quien le parezca básica la duda, pero me gustaría aclararla.
A estas alturas sé que hay ya varios hilos antiguos donde se habla del dither y en los que la teoría queda muy clarita. El caso, es que ayer hice un par de pruebas de exportación y no me queda tan claro que esa teoría sea aplicable en el 100% de los casos. Así que deseo abrir debate entorno a unas capturas de pantalla que paso a compartir.
Por un lado quise ver las diferencias al pasar a distintas frecuencias de muestreo. Mi conclusión es que 44 y 48 KHz son muy semejantes y la diferencia respecto a 96 KHz es abismal. Así pues, siempre que el destino no sea CD (44.1 máximo) o MP3 (48 KHz máximo), un archivo FLAC o MP4 (para Internet) lo dejaría a 96 KHz para guardar la calidad. Esa conclusión va en la línea de un productor de música clásica noruego que lleva un estudio llamado 2L, que afirmaba que en pruebas de doble ciego no es perceptible la conversión de 192 a 96, pero sí de 96 a 48 (lo mismo con 172-88 y 88-44).
Luego, pasé a ver la diferencia en la onda al introducir o no dither al convertir de 24 bits a 16 bits (conversión obligada tanto para CD como para cualquier archivo de tipo lossy). Supuestamente al hacerlo sin dither, debería producir distorsiones en la onda. Supuestamente, la teoría dice que es preferible el ruido introducido por el dither que esas supuestas distorsiones. El caso es que en la captura de pantalla que corresponde a la conversión sin dither no aprecio diferencias evidentes respecto al original, mientras que la captura de pantalla que corresponde a la conversión con dither se aprecia con perfecta claridad el ruido introducido en la onda. Hay que decir que solo cambié la tasa de bits, no la frecuencia de muestreo. Mi conclusión es que (al menos en este caso) no es buena idea usar dither.
Pregunto, ¿Puede ser porque al no haber material sonoro importante a menos de 96 dB, al pasar de los 140 dB de rango dinámico a los 96, no se produzca ninguna distorsión perceptible, haciendo injustificable el ruido introducido por el dither (que sí es levemente perceptible al oído)? Y en caso de ser eso, acaso hay algún tipo de música que use de forma efectiva ese enorme rango dinámico? Porque yo creo que ni la música clásica lo tiene. Supongo que habrá a quien le parezca básica la duda, pero me gustaría aclararla.





 , hombre, no estoy diciendo que sea de otro mundo, con "universo" me estoy refiriendo al ámbito en que aplica, el otro universo al que me refiero es el de señales transmitidas digitalmente, trenes de pulso.
, hombre, no estoy diciendo que sea de otro mundo, con "universo" me estoy refiriendo al ámbito en que aplica, el otro universo al que me refiero es el de señales transmitidas digitalmente, trenes de pulso.


