Gracias AGK por tu valiosa información. He consultado el índice del libro del profesor Goldáraz que me has recomendado. Lo que más me ha interesado, y creo que le voy a seguir el rastro, es su Anexo IV, titulado: Razones y cents. Un saludo, José Candela Castillo
Semitonos en la escala diatónica

OFERTAS Ver todas
-
-29%UA Apollo x6 Gen2 Essentials+
-
-9%ADJ myDMX5
-
-30%Behringer X32 Producer
 mod
mod
Había escrito una justificación matemática más extensa, comparando tu propuesta (no correcta) y lo que te insistimos en presentar Vagar y yo (que no es nuestro, sino la definición rigurosa que está desde hace siglos en infinidad de libros). Pero para no hacerlo tan largo presento una paradoja, que es un método válido de refutación.
Si tu propuesta fuera correcta, debería ser resistente al estudio de otros dos intervalos en el que uno sea de doble extensión al otro.
Aplícalo al caso de la octava. Toma estos tres 'la' (que ya te dije antes podías estudiar para rebatirte a tí mismo) : 220 - 440 - 880 Hz.
De 220 a 440 hay una octava, y la distancia en Hz es de 220. De 220 a 880 hay dos octavas y las distancia en Hz es de 660. Según tu propuesta, el cociente de esas dos diferencias debería ser dos (o 'aproximadamente' dos). Pero 660/220 = 3. Que espero sí te parezca suficientemente no próximo a 2.
El 0,54 del que hablabas sólo aparenta ser 'próximo' a lo que quieres encontrar, pero no lo es. Tiene el mismo vicio que ese otro análisis de una frente a dos octavas. Pero al usar uno y dos semitonos, las diferencias (que crecen exponencialmente a medida que crece el intervalo) aún no han podido llegar a ser mayores. Pero son igual de graves en su origen y en la confusión a la que llevan.
Si tu propuesta fuera correcta, debería ser resistente al estudio de otros dos intervalos en el que uno sea de doble extensión al otro.
Aplícalo al caso de la octava. Toma estos tres 'la' (que ya te dije antes podías estudiar para rebatirte a tí mismo) : 220 - 440 - 880 Hz.
De 220 a 440 hay una octava, y la distancia en Hz es de 220. De 220 a 880 hay dos octavas y las distancia en Hz es de 660. Según tu propuesta, el cociente de esas dos diferencias debería ser dos (o 'aproximadamente' dos). Pero 660/220 = 3. Que espero sí te parezca suficientemente no próximo a 2.
El 0,54 del que hablabas sólo aparenta ser 'próximo' a lo que quieres encontrar, pero no lo es. Tiene el mismo vicio que ese otro análisis de una frente a dos octavas. Pero al usar uno y dos semitonos, las diferencias (que crecen exponencialmente a medida que crece el intervalo) aún no han podido llegar a ser mayores. Pero son igual de graves en su origen y en la confusión a la que llevan.

Hola Pablo, Todo mi agradecimiento por darle cierta importancia a mi ejercicio en cierto modo provocador de ayer. Los elementos de tus respuestas de ayer ya supusieron una buena lección para mí y te lo agradezco.
Le he dado una lectura ahora mismo pero voy a estudiar con detalle esta nueva respuesta tuya.
Entretanto, me permito someterte un proyecto de texto, esta vez un poco más reflexivo, que debería en su versión final presentar a mi profesor de Composición. Si tienes alguna corrección que hacerme a ese texto (sobre todo en la parte matemática, te lo agradecería enormemte. No tienes porqué, por supuesto, responderme pero si piensas hacerlo, no hay prisa. Tengo que entregar el texto sólo la semana que viene.
El esbozo de texto es el siguiente: "La respuesta completa a la pregunta frecuente de porqué entre Mi y Fa hay un un intervalo al que se le denomina semitono debe tener, como mínimo, un doble carácter: científico (Matemáticas y Física Acústica) y cultural (Musicología). Como la pregunta se refiere a la escala diatónica occidental de siete notas (Do a SI), esa respuesta completa podría ser la siguiente. El proceso de formalización del círculo de quintas que empezando en el monocordio de Pitágoras se ha usado para hallar esas siete notas usa una determinada progresión geométrica y realiza la ubicación de las mismas dentro de una misma octava (delimitada por un sonido y su doble en la ascensión de grave a agudo o su mitad en el descenso de agudo a grave). Así se ha logrado numerizar una serie de sonidos más o menos armoniosos. Pues bien, la primera interrupción significativa del orden repetitivo de la serie de números racionales (quebrados) resultante aparece entre las notas 3ª y 4ª (Mi y Fa en la escala mayor de DO). Dicha interrupción aparece cuando al valor racional de los dos intervalos anteriores a MI de esa escala (de DO a RE y de RE a MI), que es de 9:8 (ó 1,125), le sucede un valor del tercer intervalo (de MI a FA) que es distinto, a saber, 256:243 (ó 1,053). Lo mismo que acabamos de ver para el primer tetracordio de la octava de la escala diatónica (grupos de notas DO, RE, MI y FA) ocurre en el segundo tetracordio (grupo de notas FA, SOL, LA y SI y sus respectivos intervalos subsiguientes), donde el intervalo de FA a SOL y el de SOL a LA tienen un valor distinto al del intervalo de Si a DO de la octava siguiente (de nuevo, 1,125 y 1,053 respectivamente). Se puede constatar que si unimos los dos intervalos diferentes obtenemos, aproximadamente, el valor de cada uno de los restantes cinco intervalos, es decir: (256:243) ² ≈ 9:8 (1,109 ≈ 1,125). ¿Podría seguirse de esta adición la atribución del nombre “tono” (“tensión” en griego) a los citados cinco intervalos y de semitono a los dos restantes (MI a FA y SI a DO) ? "
Le he dado una lectura ahora mismo pero voy a estudiar con detalle esta nueva respuesta tuya.
Entretanto, me permito someterte un proyecto de texto, esta vez un poco más reflexivo, que debería en su versión final presentar a mi profesor de Composición. Si tienes alguna corrección que hacerme a ese texto (sobre todo en la parte matemática, te lo agradecería enormemte. No tienes porqué, por supuesto, responderme pero si piensas hacerlo, no hay prisa. Tengo que entregar el texto sólo la semana que viene.
El esbozo de texto es el siguiente: "La respuesta completa a la pregunta frecuente de porqué entre Mi y Fa hay un un intervalo al que se le denomina semitono debe tener, como mínimo, un doble carácter: científico (Matemáticas y Física Acústica) y cultural (Musicología). Como la pregunta se refiere a la escala diatónica occidental de siete notas (Do a SI), esa respuesta completa podría ser la siguiente. El proceso de formalización del círculo de quintas que empezando en el monocordio de Pitágoras se ha usado para hallar esas siete notas usa una determinada progresión geométrica y realiza la ubicación de las mismas dentro de una misma octava (delimitada por un sonido y su doble en la ascensión de grave a agudo o su mitad en el descenso de agudo a grave). Así se ha logrado numerizar una serie de sonidos más o menos armoniosos. Pues bien, la primera interrupción significativa del orden repetitivo de la serie de números racionales (quebrados) resultante aparece entre las notas 3ª y 4ª (Mi y Fa en la escala mayor de DO). Dicha interrupción aparece cuando al valor racional de los dos intervalos anteriores a MI de esa escala (de DO a RE y de RE a MI), que es de 9:8 (ó 1,125), le sucede un valor del tercer intervalo (de MI a FA) que es distinto, a saber, 256:243 (ó 1,053). Lo mismo que acabamos de ver para el primer tetracordio de la octava de la escala diatónica (grupos de notas DO, RE, MI y FA) ocurre en el segundo tetracordio (grupo de notas FA, SOL, LA y SI y sus respectivos intervalos subsiguientes), donde el intervalo de FA a SOL y el de SOL a LA tienen un valor distinto al del intervalo de Si a DO de la octava siguiente (de nuevo, 1,125 y 1,053 respectivamente). Se puede constatar que si unimos los dos intervalos diferentes obtenemos, aproximadamente, el valor de cada uno de los restantes cinco intervalos, es decir: (256:243) ² ≈ 9:8 (1,109 ≈ 1,125). ¿Podría seguirse de esta adición la atribución del nombre “tono” (“tensión” en griego) a los citados cinco intervalos y de semitono a los dos restantes (MI a FA y SI a DO) ? "
 mod
mod
Personalmente cuando veo cosas como 256:243 solo veo un empeño nada interesante en forzar una apariencia de fundamento matemático que no tiene mucho sentido perceptual.
El problema, que es sobre el que trataba de reflexionar ese texto divulgativo mío que te señaló Vagar, es que, aunque es cierto que algunos elementos muy básicos de los que construyen la música tienen un fundamento físico /matemático, otros muchos (vencedores en cantidad) no lo tienen. Son resultado de la práctica musical y de su deseo de ir más allá del corsé y los elementos triviales que sí tienen un fácil anclaje matemático.
Pero como las matemáticas son tan atractivas hay quien busca y rebusca hasta dar con unos números que parezcan justificar lo que en realidad tiene otras razones.
En la serie armónica y con los instrumentos y sonidos más habituales, suelen ser los primeros armónicos los más destacados. El solapamiento en alto grado de las series armónicas de dos sonidos es lo que genera esa sensación que llamamos consonancia. Pero la percepción de esa relación está más concentrada en los primeros armónicos. Cuanto más te alejas del fundamental, suelen tener menos nivel. Y, sobre todo, suelen venir más 'concentrados' en la posición que es sensible a ellos en la cóclea.
La mayor parte de los modelos de audición describen la descomposición de los estímulos sonoros en la cóclea en términos de un análisis de tipo Q constante. Es decir, a modo de un banco de filtros de anchura relativa constante. Cuanto más alta es la frecuencia, mayor es la anchura del filtro (lo que se mantiene constante es la ratio entre fmax - fmin entre fcentral en cada banda). O dicho de otra forma, mientras en los armónicos primeros existe capacidad en la cóclea para separar sus estímulos, los medios y altos no pueden resolverse, no pueden separarse, son sentidos de forma agregada en la región correspondiente de la cóclea. Se puede ver físicamente que es así en experimentos con cócleas (de ratón, normalmente ).
).
Así que buscar una ratio entre el armónico 256 y el 243... No hay resolución suficiente en el análisis frecuencial del oído para resolverlos. Se escuchan en grupo con otros cercanos.
De hecho esa escucha grupal de los armónicos altos de cualquier nota hace que lo que se perciba sea el batido que se forma entre ellos, que resulta ser a la frecuencia fundamental. Eso refuerza el que se oiga la nota a la que la serie corresponde y no sus 'partes'.
Es en los primeros armónicos donde si hay capacidad de escucha separada y por tanto donde se concentra más la sensación de consonancia. Por eso las distancias entre los muy primeros armónicos son relevantes y sí pueden usarse ratios enteras con números bajos que tengan cierta credibilidad como forma matemática de expresar un hecho preceptual. Si dos notas guardan esas distancias y relaciones enteras y con números bajos, tienen más fácil generar sensaciones consonantes.
Es el caso de la quinta justa (ratio 3/2), puedes verlo en ese texto, dando lugar a que uno de cada dos armónicos de sol ya esté presente en el do que está una quinta por debajo (el tercer armónico de do y el segundo de sol se solapan, y así también el sexto y cuarto, el noveno y sexto, etc.). O uno de cada tres de fa con su do inferior Y uno de cada cuatro en mi con do, etc. De nuevo lo puedes ver en ese texto.
Parece (y es, ciertamente) atractivo, llamativo. Pero ese camino tiene muy poco recorrido.
A medida que subimos en el orden de armónico las frecuencias empiezan a no coincidir tan bien con las 12 notas que usamos en la octava. Y está esa otra cuestión que te comentaba de que ya dejamos de desarrollar en la cóclea los armónicos aislados y solo los podemos sentir en racimos, con lo que no cabe hablar de sentir 'un' concreto armónico de esos tan altos (salvo que esté atípicamente reforzado con una resonancia y pase a ser casi un estímulo disociado, una nota por si mismo).
Igual te estoy liando más que ayudando. En ciencia uno de los muchos criterios para considerar la validez de una teoría es que sea sencilla. Las cosas muchas veces admiten explicaciones sencillas si se da con el modelo correcto. Si la explicación empieza a complicarse existe el deber de plantearse que quizá lo que falla es el modelo.
El modelo de cocientes enteros y de pensar en distancias entre armónicos, etc. vale en la muy primera parte. No le veo sentido perceptual a extenderlo mucho más allá de los primeros armónicos (y muy pocos, no más de la primera docena, te diría). Se ha usado ese sistema con números mayores, es cierto y lo verás en algunos libros, para buscar justificaciones solo desde la matemática y no tanto desde la percepción, que me parecen exageradamente forzadas, un intento de bañar del prestigio de la matemática a algo que no lo necesita porque tiene su propio mundo (para mí la música es ante todo un fenómeno auditivo, para ser percibido, no algo estrictamente físico o matemático, y cualquier análisis debe conocer y partir de lo que se percibe).
Se ha usado también eso de las ratios con cifras demasiado altas para construir escalas sólo desde la matemática y construir lenguajes musicales (muy distantes al tonal convencional) aprovechando ciertas virtudes de las relaciones matemáticas, y tratando de usar esas estructuras y sus contrastes para otros lenguajes.
La escala de temperamento igual surge como una forma (lo que te decía Vagar) de cerrar un ciclo por las doce notas que sea cerrado y que se base en un único principio. Cerrado para quedarnos en un mundo de doce notas, y con regla única porque eso permite moverse con unas mismas reglas entre unas y otras partes de ese mundo de doce (poder modular a diferentes tonalidades usando un juego de doce notas sin tenerlas que adaptar y corregir en cada momento a la tonalidad del fragmento). La forma de lograrlo es no seguir el ciclo de quintas naturales (que no 'vuelve' a do tras doce saltos). Corrigiendo los saltos para que tras doce pasos de 'quinta' (no justa, sino 'temperada', para entendernos) se retorne a un do, las doce notas quedan, si las ordenamos cromáticamente, separadas por saltos iguales. El semitono que se usa en la escala de temperamento igual. Y que implica multiplicar la frecuencia anterior por la raíz doceava de dos, garantizando así que tras doce saltos de esa quinta corregida volvamos a la nota original, aunque sea en otra octava, y cerremos el círculo.
El que de esos doce sonidos hayamos escogido 7 y que esos siete sean los que son, tiene otras razones. Más propias de la decisión humana que de la imposición de las matemáticas.
En buena medida como una nota y su quinta y cuarta justas son las notas más hermanas, esas tres aparecen en muchas culturas como notas esenciales. Como los primeros armónicos de cada nota contienen además de la propia nota, su quinta y su tercera mayor, es también creíble y visible en muchas culturas el uso de esas tres notas (las más fáciles de generar soplando un tubo). Y si desarrollas tónica, tercera y quinta desde do, sol y fa (que serían los 'tubos' que mejor combinan en un sentido consonante) resulta que obtienes las siete notas de la escala mayor. Hasta ahí se puede intentar una justificación medio 'naturalista', pero ya un tanto forzada.
La música por suerte es mucho más rica que estos artificios matemáticos y recoge las decisiones, búsquedas y creatividad de los humanos. No sólo las restricciones de los tubos. Tubos que hemos ido complicando hacia toda suerte de instrumentos para ir más allá de los cuernos primitivos.
Menudo rollo te he metido y posiblemente sin contestar tu pregunta. Pero te hablo de lo que sé o creo saber. Y de lo de la etimología de 'tono' no soy yo quien te puede dar mejor luz.
Espero que al menos te haya interesado.
El problema, que es sobre el que trataba de reflexionar ese texto divulgativo mío que te señaló Vagar, es que, aunque es cierto que algunos elementos muy básicos de los que construyen la música tienen un fundamento físico /matemático, otros muchos (vencedores en cantidad) no lo tienen. Son resultado de la práctica musical y de su deseo de ir más allá del corsé y los elementos triviales que sí tienen un fácil anclaje matemático.
Pero como las matemáticas son tan atractivas hay quien busca y rebusca hasta dar con unos números que parezcan justificar lo que en realidad tiene otras razones.
En la serie armónica y con los instrumentos y sonidos más habituales, suelen ser los primeros armónicos los más destacados. El solapamiento en alto grado de las series armónicas de dos sonidos es lo que genera esa sensación que llamamos consonancia. Pero la percepción de esa relación está más concentrada en los primeros armónicos. Cuanto más te alejas del fundamental, suelen tener menos nivel. Y, sobre todo, suelen venir más 'concentrados' en la posición que es sensible a ellos en la cóclea.
La mayor parte de los modelos de audición describen la descomposición de los estímulos sonoros en la cóclea en términos de un análisis de tipo Q constante. Es decir, a modo de un banco de filtros de anchura relativa constante. Cuanto más alta es la frecuencia, mayor es la anchura del filtro (lo que se mantiene constante es la ratio entre fmax - fmin entre fcentral en cada banda). O dicho de otra forma, mientras en los armónicos primeros existe capacidad en la cóclea para separar sus estímulos, los medios y altos no pueden resolverse, no pueden separarse, son sentidos de forma agregada en la región correspondiente de la cóclea. Se puede ver físicamente que es así en experimentos con cócleas (de ratón, normalmente
Así que buscar una ratio entre el armónico 256 y el 243... No hay resolución suficiente en el análisis frecuencial del oído para resolverlos. Se escuchan en grupo con otros cercanos.
De hecho esa escucha grupal de los armónicos altos de cualquier nota hace que lo que se perciba sea el batido que se forma entre ellos, que resulta ser a la frecuencia fundamental. Eso refuerza el que se oiga la nota a la que la serie corresponde y no sus 'partes'.
Es en los primeros armónicos donde si hay capacidad de escucha separada y por tanto donde se concentra más la sensación de consonancia. Por eso las distancias entre los muy primeros armónicos son relevantes y sí pueden usarse ratios enteras con números bajos que tengan cierta credibilidad como forma matemática de expresar un hecho preceptual. Si dos notas guardan esas distancias y relaciones enteras y con números bajos, tienen más fácil generar sensaciones consonantes.
Es el caso de la quinta justa (ratio 3/2), puedes verlo en ese texto, dando lugar a que uno de cada dos armónicos de sol ya esté presente en el do que está una quinta por debajo (el tercer armónico de do y el segundo de sol se solapan, y así también el sexto y cuarto, el noveno y sexto, etc.). O uno de cada tres de fa con su do inferior Y uno de cada cuatro en mi con do, etc. De nuevo lo puedes ver en ese texto.
Parece (y es, ciertamente) atractivo, llamativo. Pero ese camino tiene muy poco recorrido.
A medida que subimos en el orden de armónico las frecuencias empiezan a no coincidir tan bien con las 12 notas que usamos en la octava. Y está esa otra cuestión que te comentaba de que ya dejamos de desarrollar en la cóclea los armónicos aislados y solo los podemos sentir en racimos, con lo que no cabe hablar de sentir 'un' concreto armónico de esos tan altos (salvo que esté atípicamente reforzado con una resonancia y pase a ser casi un estímulo disociado, una nota por si mismo).
Igual te estoy liando más que ayudando. En ciencia uno de los muchos criterios para considerar la validez de una teoría es que sea sencilla. Las cosas muchas veces admiten explicaciones sencillas si se da con el modelo correcto. Si la explicación empieza a complicarse existe el deber de plantearse que quizá lo que falla es el modelo.
El modelo de cocientes enteros y de pensar en distancias entre armónicos, etc. vale en la muy primera parte. No le veo sentido perceptual a extenderlo mucho más allá de los primeros armónicos (y muy pocos, no más de la primera docena, te diría). Se ha usado ese sistema con números mayores, es cierto y lo verás en algunos libros, para buscar justificaciones solo desde la matemática y no tanto desde la percepción, que me parecen exageradamente forzadas, un intento de bañar del prestigio de la matemática a algo que no lo necesita porque tiene su propio mundo (para mí la música es ante todo un fenómeno auditivo, para ser percibido, no algo estrictamente físico o matemático, y cualquier análisis debe conocer y partir de lo que se percibe).
Se ha usado también eso de las ratios con cifras demasiado altas para construir escalas sólo desde la matemática y construir lenguajes musicales (muy distantes al tonal convencional) aprovechando ciertas virtudes de las relaciones matemáticas, y tratando de usar esas estructuras y sus contrastes para otros lenguajes.
La escala de temperamento igual surge como una forma (lo que te decía Vagar) de cerrar un ciclo por las doce notas que sea cerrado y que se base en un único principio. Cerrado para quedarnos en un mundo de doce notas, y con regla única porque eso permite moverse con unas mismas reglas entre unas y otras partes de ese mundo de doce (poder modular a diferentes tonalidades usando un juego de doce notas sin tenerlas que adaptar y corregir en cada momento a la tonalidad del fragmento). La forma de lograrlo es no seguir el ciclo de quintas naturales (que no 'vuelve' a do tras doce saltos). Corrigiendo los saltos para que tras doce pasos de 'quinta' (no justa, sino 'temperada', para entendernos) se retorne a un do, las doce notas quedan, si las ordenamos cromáticamente, separadas por saltos iguales. El semitono que se usa en la escala de temperamento igual. Y que implica multiplicar la frecuencia anterior por la raíz doceava de dos, garantizando así que tras doce saltos de esa quinta corregida volvamos a la nota original, aunque sea en otra octava, y cerremos el círculo.
El que de esos doce sonidos hayamos escogido 7 y que esos siete sean los que son, tiene otras razones. Más propias de la decisión humana que de la imposición de las matemáticas.
En buena medida como una nota y su quinta y cuarta justas son las notas más hermanas, esas tres aparecen en muchas culturas como notas esenciales. Como los primeros armónicos de cada nota contienen además de la propia nota, su quinta y su tercera mayor, es también creíble y visible en muchas culturas el uso de esas tres notas (las más fáciles de generar soplando un tubo). Y si desarrollas tónica, tercera y quinta desde do, sol y fa (que serían los 'tubos' que mejor combinan en un sentido consonante) resulta que obtienes las siete notas de la escala mayor. Hasta ahí se puede intentar una justificación medio 'naturalista', pero ya un tanto forzada.
La música por suerte es mucho más rica que estos artificios matemáticos y recoge las decisiones, búsquedas y creatividad de los humanos. No sólo las restricciones de los tubos. Tubos que hemos ido complicando hacia toda suerte de instrumentos para ir más allá de los cuernos primitivos.
Menudo rollo te he metido y posiblemente sin contestar tu pregunta. Pero te hablo de lo que sé o creo saber. Y de lo de la etimología de 'tono' no soy yo quien te puede dar mejor luz.
Espero que al menos te haya interesado.
 mod
mod
Intentaré ser más claro, cosa más fácil tras haber comentado lo anterior.
La supuesta irregularidad que encuentras entre mi y fa no es la verdadera irregularidad. Todas las notas salen (todas, las doce) de aplicar con total regularidad saltos de quinta 'temperada'. Si completas los doce saltos de quinta llegas a la escala cromática de temperamento igual. Que no tiene irregularidades.
Lo que es 'irregular' es pararse tras seis saltos y no continuar con la otra parte del recorrido (al menos mientras no te dediques al dodecadonismo ) . Y como resultado de ese parón, las siete notas que resultan no completan la regularidad de la escala cromática y tienen esa distribución conocida tono tono semitono tono tono tono semitono.
) . Y como resultado de ese parón, las siete notas que resultan no completan la regularidad de la escala cromática y tienen esa distribución conocida tono tono semitono tono tono tono semitono.
Y la respuesta no es matemática. Es curioso, y no conozco estudios que justifiquen sólidamente la razón, que muchas culturas han elegido escalas de siete notas dentro de la octava (las 'nuestras' u otras). Pero en otras hay escalas de cinco. O se usan escalas con sonidos elegidos sobre una división de la octava en más de doce partes...
Nuestra elección de siete, y de esas siete como modelo canónico (la escala mayor) desde la que definimos y usamos otras, no deja de ser un convenio, una práctica. Que encaja bien con el tipo de lenguaje musical tonal, al que se llega desde las prácticas anteriores. Permite tener asimetría en la escala, que es esencial para que puedan aparecer diferencias de rol entre los grados y por tanto pueda surgir un elemento como referente (el centro tonal). Cuenta con mecanismos como el trítono entre cuarto y séptimo grados, que suena en el acorde el quinto grado, haciendo que ese grado 'hermano' quiera volver y resolver esas notas hacia el acorde de tónica generando un movimiento robusto y fácil de reconocer... Y mil cosas más que son elementos característicos de lo tonal.
La matemática, creo, es solo uno de los elementos de una realidad que es multidisciplinaria y multicausal. No intentes usarla como único argumento. Hay otras dimensiones necesarias para la respuesta que buscas.
La supuesta irregularidad que encuentras entre mi y fa no es la verdadera irregularidad. Todas las notas salen (todas, las doce) de aplicar con total regularidad saltos de quinta 'temperada'. Si completas los doce saltos de quinta llegas a la escala cromática de temperamento igual. Que no tiene irregularidades.
Lo que es 'irregular' es pararse tras seis saltos y no continuar con la otra parte del recorrido (al menos mientras no te dediques al dodecadonismo
Y la respuesta no es matemática. Es curioso, y no conozco estudios que justifiquen sólidamente la razón, que muchas culturas han elegido escalas de siete notas dentro de la octava (las 'nuestras' u otras). Pero en otras hay escalas de cinco. O se usan escalas con sonidos elegidos sobre una división de la octava en más de doce partes...
Nuestra elección de siete, y de esas siete como modelo canónico (la escala mayor) desde la que definimos y usamos otras, no deja de ser un convenio, una práctica. Que encaja bien con el tipo de lenguaje musical tonal, al que se llega desde las prácticas anteriores. Permite tener asimetría en la escala, que es esencial para que puedan aparecer diferencias de rol entre los grados y por tanto pueda surgir un elemento como referente (el centro tonal). Cuenta con mecanismos como el trítono entre cuarto y séptimo grados, que suena en el acorde el quinto grado, haciendo que ese grado 'hermano' quiera volver y resolver esas notas hacia el acorde de tónica generando un movimiento robusto y fácil de reconocer... Y mil cosas más que son elementos característicos de lo tonal.
La matemática, creo, es solo uno de los elementos de una realidad que es multidisciplinaria y multicausal. No intentes usarla como único argumento. Hay otras dimensiones necesarias para la respuesta que buscas.

Muchas gracias Pablo por tu inestimable y valiosa lección, una vez más.
Siguiendo tu fundada crítica, te propongo substituir la expresión "primera interrupción significativa" por "una interrupción significativa al respecto de la respuesta a la pregunta objeto de este texto...".
En cuanto a tu frase: "Así que buscar una ratio entre el armónico 256 y el 243... No hay resolución suficiente en el análisis frecuencial del oído para resolverlos. Se escuchan en grupo con otros cercanos." Perdona pero no la entiendo porque, a lo mejor es por mi ignorancia en estos temas pero yo no he pretendido (que yo sepa) "buscar una ratio entre del armónico 256 y el 243". Entonces, si lo aceptas, no voy a tener en cuenta esta observación, por otra parte muy autorizada como es lógico.
Perdona si insisto pero el siguiente texto "(256:243) ² ≈ 9:8 (1,109 ≈ 1,125)" está bien o no ? Es que la he sacado de aquí: http://www.xtec.cat/centres/a8019411/caixa/escalas.htm y no me fío mucho de este artículo por la forma en que está redactado: poco clara la relación entre los cuadros excel y los textos explicativos correspondientes).
Pasando a la parte cultural-musicológica, en una tesis doctoral sobre la historia del monocordio que acabo de encontrar (https://www.tdx.cat/bitstream/handle/10803/126116/tccu.pdf?sequence=1), se dice que la ratio 256:243 la han llamado de diferente manera los tratadistas renacentistas que recuperaron a Pitágoras (ver foto adjunta), por lo que creo que voy a limitar el campo de mi estudio a la limma griega para terminar en el "semitonium" de Boecio, primera utilización historiográfica significativa del término semitono.
En todo caso, gracias sinceramente por dedicarme tanto tiempo. Se te nota, como has dicho tú, tu pasión. Sólo con pasión, decía Hegel, se hace algo grande (y no olvidemos que pasión y paciencia tienen la misma raíz: el πάθος griego).
Siguiendo tu fundada crítica, te propongo substituir la expresión "primera interrupción significativa" por "una interrupción significativa al respecto de la respuesta a la pregunta objeto de este texto...".
En cuanto a tu frase: "Así que buscar una ratio entre el armónico 256 y el 243... No hay resolución suficiente en el análisis frecuencial del oído para resolverlos. Se escuchan en grupo con otros cercanos." Perdona pero no la entiendo porque, a lo mejor es por mi ignorancia en estos temas pero yo no he pretendido (que yo sepa) "buscar una ratio entre del armónico 256 y el 243". Entonces, si lo aceptas, no voy a tener en cuenta esta observación, por otra parte muy autorizada como es lógico.
Perdona si insisto pero el siguiente texto "(256:243) ² ≈ 9:8 (1,109 ≈ 1,125)" está bien o no ? Es que la he sacado de aquí: http://www.xtec.cat/centres/a8019411/caixa/escalas.htm y no me fío mucho de este artículo por la forma en que está redactado: poco clara la relación entre los cuadros excel y los textos explicativos correspondientes).
Pasando a la parte cultural-musicológica, en una tesis doctoral sobre la historia del monocordio que acabo de encontrar (https://www.tdx.cat/bitstream/handle/10803/126116/tccu.pdf?sequence=1), se dice que la ratio 256:243 la han llamado de diferente manera los tratadistas renacentistas que recuperaron a Pitágoras (ver foto adjunta), por lo que creo que voy a limitar el campo de mi estudio a la limma griega para terminar en el "semitonium" de Boecio, primera utilización historiográfica significativa del término semitono.
En todo caso, gracias sinceramente por dedicarme tanto tiempo. Se te nota, como has dicho tú, tu pasión. Sólo con pasión, decía Hegel, se hace algo grande (y no olvidemos que pasión y paciencia tienen la misma raíz: el πάθος griego).
 mod
mod
Ahora está mucho más claro lo que querías contar, gracias a ese enlace del artículo que has compartido.
Lo que plantea inicialmente ese artículo es, que, como es bien sabido, al ir dando saltos de quinta desde do visitamos sol, re, la, mi, si (y fíjate que paran ahí, no siguen -y ya tienen un salto entre el 'si' y el 'do' que es 'diferente', que ha salido 'rana' ). Han creado dos grupos (do,re,mi y sol,la,si) de notas que surgen de saltos de quinta justa (muy consonantes), pero no pueden completar con esa estrategia más allá: saldría más bien el fa#, y por otra parte ya te comentó Vagar que ese círculo no se cierra, no vuelve al do si lo extendiéramos.
). Han creado dos grupos (do,re,mi y sol,la,si) de notas que surgen de saltos de quinta justa (muy consonantes), pero no pueden completar con esa estrategia más allá: saldría más bien el fa#, y por otra parte ya te comentó Vagar que ese círculo no se cierra, no vuelve al do si lo extendiéramos.
Continuando con el artículo, es a la hora de incorporar la nota que falta para una escala de siete donde de buenas a primera calzan el fa siguiendo una estrategia diferente. Lo meten porque saben que suena bien y anda por ahí cerca (dicho en plan simple). Juegan con la cuarta. Y acaba apareciendo una 'excepción' más, también el paso de mi a fa es 'diferente'.
Realmente el fa es la quinta inferior de do, así que también hay implícito un salto de quinta.
En esa construcción para la escala los intervalos y 'ratios' para el avance de 'semitono' (1,053) que hay entre mi y fa y entre si y do son los que son. Surge ese semitono que no es la mitad del tono (el tono en esa forma de construir la escala es 1,125 porque surge de acumular dos quintas justas y corregir octava, y no se alcanza de forma exacta acumulando dos semitonos de los que han incorporado con valor 1,053 porque 1,053·1,053 es 1,109 y no 1,125).
Esa diferencia es un resultado de la falta de cierre del círculo. Si siguieran subiendo no llegarían a do. Así que siguen con las quintas pero al revés, hacia abajo (o como lo dicen en el artículo, siguen con cuartas) para que aparezca fa y también las notas alteradas.
Pero de nuevo se paran. Meten fa y los cinco sonidos alterados y paran.
Paran porque si siguen se hace evidente que ese movimiento no se cierra.
Hasta ahí bien, es una forma como otra cualquiera de crear una escala. Se basa en quintas pero tiene un alcance limitado, no pueden extender sin límite la estrategia porque salen 'otras' notas, no se queda en las doce habituales.
Reflejo de esa falta de simetría, el intervalo 'semi' no es exactamente la mitad.
Lo que ya no me gusta (puede ser opinable) es ahora empeñarse en que 1,109 es aproximadamente 1,125. ¿Para qué? ¿Para sentirse cómodos con llamarlo 'semi'? Vale. Pero dar por buena esa aproximación (igualar lo que no es igual) equivale para mi gusto a intentar borrar el hecho diferencial de cómo se construye esa escala. Es mas o menos la mitad, sí. Pero en que no lo sea exactamente radica la la justificación de los aspectos positivos y negativos que encierra esa escala (buena consonancia en sus intervalos básicos, pero problemas para modular a otros tonos manteniendo esas mismas afinaciones, etc...).
La escala cromática, como también dice ese artículo, reparte la corrección por igual en los doce saltos de semitono de la escala cromática, con los objetivos que ya hemos mencionado en mensajes anteriores y da lugar al semitono de 1,059 y al tono de 1,059·1,059 y a una quinta que ya no es 'justa' sino que viene un poco 'crispada', etc. Sus propios pros y contras.
No sé lo que te preguntaban en ese trabajo de la asignatura, que has mencionado en algún comentario. Pero yo veo más interesante contar las dos y sus pros y contras que empeñarse en convertir en igual lo que no lo es. Por eso hay esas dos (entre otras muchas) formas de realizar la escala.
Se aprende más de saber que hay esas variantes y sus diferencias, sus razones y sus usos.
Vamos que sí, que es 'cercano' a la mitad y por tanto se puede hablar de semi, pero que en esa escala es imprescindible que no sea exactamente 'semi' y por tanto una pena acabar tanto análisis con algo como ese 'aproximadamente igual'.
Lo que plantea inicialmente ese artículo es, que, como es bien sabido, al ir dando saltos de quinta desde do visitamos sol, re, la, mi, si (y fíjate que paran ahí, no siguen -y ya tienen un salto entre el 'si' y el 'do' que es 'diferente', que ha salido 'rana'
Continuando con el artículo, es a la hora de incorporar la nota que falta para una escala de siete donde de buenas a primera calzan el fa siguiendo una estrategia diferente. Lo meten porque saben que suena bien y anda por ahí cerca (dicho en plan simple). Juegan con la cuarta. Y acaba apareciendo una 'excepción' más, también el paso de mi a fa es 'diferente'.
Realmente el fa es la quinta inferior de do, así que también hay implícito un salto de quinta.
En esa construcción para la escala los intervalos y 'ratios' para el avance de 'semitono' (1,053) que hay entre mi y fa y entre si y do son los que son. Surge ese semitono que no es la mitad del tono (el tono en esa forma de construir la escala es 1,125 porque surge de acumular dos quintas justas y corregir octava, y no se alcanza de forma exacta acumulando dos semitonos de los que han incorporado con valor 1,053 porque 1,053·1,053 es 1,109 y no 1,125).
Esa diferencia es un resultado de la falta de cierre del círculo. Si siguieran subiendo no llegarían a do. Así que siguen con las quintas pero al revés, hacia abajo (o como lo dicen en el artículo, siguen con cuartas) para que aparezca fa y también las notas alteradas.
Pero de nuevo se paran. Meten fa y los cinco sonidos alterados y paran.
Paran porque si siguen se hace evidente que ese movimiento no se cierra.
Hasta ahí bien, es una forma como otra cualquiera de crear una escala. Se basa en quintas pero tiene un alcance limitado, no pueden extender sin límite la estrategia porque salen 'otras' notas, no se queda en las doce habituales.
Reflejo de esa falta de simetría, el intervalo 'semi' no es exactamente la mitad.
Lo que ya no me gusta (puede ser opinable) es ahora empeñarse en que 1,109 es aproximadamente 1,125. ¿Para qué? ¿Para sentirse cómodos con llamarlo 'semi'? Vale. Pero dar por buena esa aproximación (igualar lo que no es igual) equivale para mi gusto a intentar borrar el hecho diferencial de cómo se construye esa escala. Es mas o menos la mitad, sí. Pero en que no lo sea exactamente radica la la justificación de los aspectos positivos y negativos que encierra esa escala (buena consonancia en sus intervalos básicos, pero problemas para modular a otros tonos manteniendo esas mismas afinaciones, etc...).
La escala cromática, como también dice ese artículo, reparte la corrección por igual en los doce saltos de semitono de la escala cromática, con los objetivos que ya hemos mencionado en mensajes anteriores y da lugar al semitono de 1,059 y al tono de 1,059·1,059 y a una quinta que ya no es 'justa' sino que viene un poco 'crispada', etc. Sus propios pros y contras.
No sé lo que te preguntaban en ese trabajo de la asignatura, que has mencionado en algún comentario. Pero yo veo más interesante contar las dos y sus pros y contras que empeñarse en convertir en igual lo que no lo es. Por eso hay esas dos (entre otras muchas) formas de realizar la escala.
Se aprende más de saber que hay esas variantes y sus diferencias, sus razones y sus usos.
Vamos que sí, que es 'cercano' a la mitad y por tanto se puede hablar de semi, pero que en esa escala es imprescindible que no sea exactamente 'semi' y por tanto una pena acabar tanto análisis con algo como ese 'aproximadamente igual'.
 mod
mod
Y por cieto muchas gracias por esa mención a la raíz común de pasión y paciencia. No lo sabía. Y da para mucho juego.
Cuando siempre se habla de la urgencia de la pasión amorosa, está claro que se habla de otra forma de pasión que no es la vocacional. Y en realidad casi siempre hay que tener mucha paciencia para llegar a veces a disfrutar de la pasión, tanto de la amorosa como de la vocacional. En fin... Mejor vuelta a los 'semi'.
Cuando siempre se habla de la urgencia de la pasión amorosa, está claro que se habla de otra forma de pasión que no es la vocacional. Y en realidad casi siempre hay que tener mucha paciencia para llegar a veces a disfrutar de la pasión, tanto de la amorosa como de la vocacional. En fin... Mejor vuelta a los 'semi'.

Fenomenal respuesta, Pablo.
La compro entera y la tendré muy en cuenta en la redacción final.
A mi pregunta anterior a la corrección de la formulación numérica final, no te preocupes en contestar: lo he consultado con mi hijo Pablo, que es profesor de matemáticas en la Autónoma y me ha recomendado escribirla así: (256:243) ² ≈ 9:8 (es decir, 1,110 ≈ 1,125), cosa que voy a hacer.
La compro entera y la tendré muy en cuenta en la redacción final.
A mi pregunta anterior a la corrección de la formulación numérica final, no te preocupes en contestar: lo he consultado con mi hijo Pablo, que es profesor de matemáticas en la Autónoma y me ha recomendado escribirla así: (256:243) ² ≈ 9:8 (es decir, 1,110 ≈ 1,125), cosa que voy a hacer.
 mod
mod
No me lo compres sin releerlo, que he corregido un poco.
Lo que había puesto no era muy exacto en un detalle, y lo he mejorado. Me dejé llevar de querer hacer un cuento bonito, pero esta mejor ahora.
El cierre del círculo sucede con el temperamento igual y permite aplicar tantos saltos de quinta (no la justa sino la de temperamento igual) hacia arriba y hacia abajo como se desee. Facilita moverse de unas notas a otras sin límite y sin que aparezcan cosas raras. Y por tanto, al modular tiene capacidad de moverse por cualquier tono manteniendo esas mismas definiciones (afinaciones) para las doce notas.
La estrategia de la quinta justa hay que pararla (sin dar mayores explicaciones) tras haber hecho do, sol, re, la, mi, si por un lado y fa, sib, mib, lab, reb, solb por el otro. Como continúes se hace evidente el no cierre de esa estrategia.
Por tanto hay que destacar (no vale callárselo cobardemente) que el movimiento está limitado. Y de forma parecida esa forma de definir las afinaciones de las doce notas, basada en quintas justas por arriba y por abajo, limita el movimiento del centro tonal, si empezamos a pensar en modulaciones. Cada vez que nos alejamos en una dirección u otra del tono do que es centro, los otros tonos piden introducir otras afinaciones, no les valen las de las quintas de do, que en esos tonos suenan menos consonantes. Y cuanto más lejos peor. Más notas quedan fuera de sitio y lo hacen de forma más notable.
El reflejo de la falta de cierre del círculo en una afinación de quintas justas es esa imposibilidad de que los intervalos entre las notas de los doce sonidos sean iguales, o eso que comentabas de que 'semi' no sea la mitad. Es una escala creada específicamente para que funcione en un tono y solo en uno, aunque en ese funcione muy bien (en el sentido de unas consonancias muy bien definidas) .
La de temperamento igual busca una solución diferente. Valer igual para cualquier centro tonal, aunque sea a costa de resultar menos perfecta en sus consonancias internas. Y con todos los semitonos iguales, como resultado de esa simetría que tiene y que le permite esa gracia de movimiento.
Lo que había puesto no era muy exacto en un detalle, y lo he mejorado. Me dejé llevar de querer hacer un cuento bonito, pero esta mejor ahora.
El cierre del círculo sucede con el temperamento igual y permite aplicar tantos saltos de quinta (no la justa sino la de temperamento igual) hacia arriba y hacia abajo como se desee. Facilita moverse de unas notas a otras sin límite y sin que aparezcan cosas raras. Y por tanto, al modular tiene capacidad de moverse por cualquier tono manteniendo esas mismas definiciones (afinaciones) para las doce notas.
La estrategia de la quinta justa hay que pararla (sin dar mayores explicaciones) tras haber hecho do, sol, re, la, mi, si por un lado y fa, sib, mib, lab, reb, solb por el otro. Como continúes se hace evidente el no cierre de esa estrategia.
Por tanto hay que destacar (no vale callárselo cobardemente) que el movimiento está limitado. Y de forma parecida esa forma de definir las afinaciones de las doce notas, basada en quintas justas por arriba y por abajo, limita el movimiento del centro tonal, si empezamos a pensar en modulaciones. Cada vez que nos alejamos en una dirección u otra del tono do que es centro, los otros tonos piden introducir otras afinaciones, no les valen las de las quintas de do, que en esos tonos suenan menos consonantes. Y cuanto más lejos peor. Más notas quedan fuera de sitio y lo hacen de forma más notable.
El reflejo de la falta de cierre del círculo en una afinación de quintas justas es esa imposibilidad de que los intervalos entre las notas de los doce sonidos sean iguales, o eso que comentabas de que 'semi' no sea la mitad. Es una escala creada específicamente para que funcione en un tono y solo en uno, aunque en ese funcione muy bien (en el sentido de unas consonancias muy bien definidas) .
La de temperamento igual busca una solución diferente. Valer igual para cualquier centro tonal, aunque sea a costa de resultar menos perfecta en sus consonancias internas. Y con todos los semitonos iguales, como resultado de esa simetría que tiene y que le permite esa gracia de movimiento.

pablofcid escribió:
Reflejo de esa falta de simetría, el intervalo 'semi' no es exactamente la mitad.
Por rizar un poco el rizo, en una escala temperada se podría decir que no es una "mitad lineal" exacta, pero sí es una "mitad logarítmica" exacta. Si se representan las frecuencias de las notas en un eje logarítmico aparecen distribuidas uniformemente:
https://www.numerickly.com/2018/12/30/frequency-domain-scale-pitches/
 mod
mod
Ese texto que has enlazado le vendrá muy bien. Seguro.
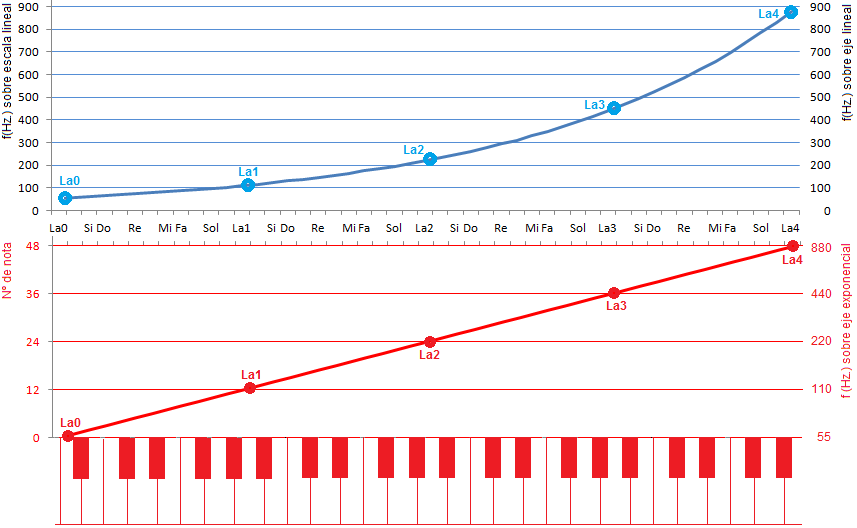
Sin salir de hispa, tenemos esta figura en ese mismo sentido:

que iba dentro de un artículo en el que las cuatro primeras secciones eran estas (igual ayudan también a José a entender mejor el rollo este de los logaritmos y demás):
Notas vs Hz: ejemplo de nuestra percepción con saltos ‘expansivos’
La fórmula de la distancia en octavas
La fórmula de la distancia en semitonos
Hz y semitonos: un ejemplo de recorrido relativo y logarítmico
El artículo era este:
https://www.hispasonic.com/tutoriales/son-decibelios-db-explicacion-para-musicos/43048
Sin salir de hispa, tenemos esta figura en ese mismo sentido:
que iba dentro de un artículo en el que las cuatro primeras secciones eran estas (igual ayudan también a José a entender mejor el rollo este de los logaritmos y demás):
Notas vs Hz: ejemplo de nuestra percepción con saltos ‘expansivos’
La fórmula de la distancia en octavas
La fórmula de la distancia en semitonos
Hz y semitonos: un ejemplo de recorrido relativo y logarítmico
El artículo era este:
https://www.hispasonic.com/tutoriales/son-decibelios-db-explicacion-para-musicos/43048

pablofcid escribió:El cierre del círculo sucede con el temperamento igual y permite aplicar tantos saltos de quinta (no la justa sino la de temperamento igual) hacia arriba y hacia abajo como se desee. Facilita moverse de unas notas a otras sin límite y sin que aparezcan cosas raras.
Por ejemplo, la conocida quinta del lobo.
https://es.wikipedia.org/wiki/Quinta_del_lobo
Ahora que tenemos, con los sintes modernos, la posibilidad de cambiar afinaciones (mi antiguo clavinova aceptaba varias de ellas) es divertido tocar piezas en algunas de ellas y comprobar como aparece el lobo...
Un saludo

Pablo y Vagar,
Pues según estas últimas aportaciones (lo que enseña numerickly y los dos gráficos de Hispasonic), que os agradezco mucho, a lo mejor mejoro el texto introduciendo una nueva expresión:
""al limma griego lo podríamos llamar "semitono logarítmico" y la adecuación del sufijo "semi" al intervalo MI-FA y SI-DO podría expresarse así: ....."
opción 1: (256:243) ² ≈ 9:8 (1,109 ≈ 1,125).
opción 2: (256:243) ² ≈ 9:8.
Me lo voy a pensar.
He aprendido mucho en estos intercambios. Muchas gracias a los dos.
Un saludo.
Pues según estas últimas aportaciones (lo que enseña numerickly y los dos gráficos de Hispasonic), que os agradezco mucho, a lo mejor mejoro el texto introduciendo una nueva expresión:
""al limma griego lo podríamos llamar "semitono logarítmico" y la adecuación del sufijo "semi" al intervalo MI-FA y SI-DO podría expresarse así: ....."
opción 1: (256:243) ² ≈ 9:8 (1,109 ≈ 1,125).
opción 2: (256:243) ² ≈ 9:8.
Me lo voy a pensar.
He aprendido mucho en estos intercambios. Muchas gracias a los dos.
Un saludo.
Nuevo post
Regístrate o identifícate para poder postear en este hilo





