Mikolopez escribió:
El oído humano tiene la habilidad de distinguir consonancia y disonancia, que en principio (sin entrar en elementos culturales) se habla de consonancia en aquellos intervalos cuya relación de frecuencias es simple (la quinta 2:3, la cuarta 3:4, la tercera mayor 4:5...).
Una pequeña puntualización, efectivamente la quinta justa "natural" o pitagórica tiene una relación de razón de dos es a tres (2:3). Vale decir si calculamos la frecuencia del Mi, que es la quinta del La (440Hz) tenemos que usar una regla de 3:
Alguien escribió:
440 = 3
X = 2
Por lo tanto:
(440 * 3) / 2 = 660
Un intervalo de quinta es justo o perfecto o consonante porque se sincronizan los periodos de ambas ondas. O sea, este intervalo produciría tres ondas, la fundamental (La) de 440Hz, la quinta (Mi) de 660Hz, y el batido (que es la mitad de la diferencia de ambas) de 110Hz. Las tres frecuencias son múltiplos o sea el fenómeno que se produce es una tercera onda periódica. Muchos creen que la quinta justa no produce batido, no es que no produzca batido, sino que el batido, la onda fundamental y la quinta tienen frecuencias múltiplos, por lo tanto, funcionan como armónicos de una nueva onda periódica, el fenómeno es como si las tres ondas se fundieran en una sola.
Pero resulta que el temperamento igual, que es el que se usa ahora en todos los instrumentos con traste, teclados e instrumentos MIDI, la quinta y la cuarta justa no tienen proporciones exactas. En estos instrumentos se usa la siguiente fórmula
F(x) = F(la) *12√2 ^ NS
o
F(x) = F(la) * 2 ^ NS/12
dónde F(la) es la frecuencia del La
y NS es el número de semitonos del intervalo
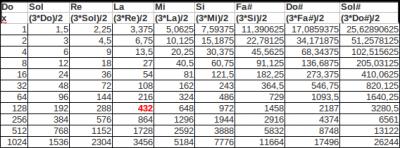
O sea si queremos calcular la frecuencia del Mi, que es la quinta del La, sabiendo que entre el Mi y el La hay 7 semitonos, aplicamos la fórmula:
Alguien escribió:
F(mi) = 440 * 12√2 ^ 7 = 440 * 2 ^ 7/12 = 659.2551
Ya de partida notamos algo extraño, a todas luces 660 no es igual que 659,2551, pero son valores muy parecidos, una diferencia casi imperceptible para un oído humano. Pero si tocamos un intervalo de quinta con un La (440Hz) y un Mi (659,2551Hz) debiera producir un batido de 109,6275Hz, o sea, aparte de las frecuencias de las notas del intervalo, debiera escucharse un sonido oscuro que es esta frecuencia de 109,6Hz
El hecho es que en la afinación actual no existen intervalos consonantes, a excepción de la octava, ningún intervalo tendría relación simple entre las frecuencias de sus notas. Dicho en palabras sencillas, que todos los intervalos debieran escucharse ligeramente desafinados.
Una pregunta sería ¿por qué los intervalos de 5 justa o 4 justa siguen sonando más agradables que intervalos como la séptima aumentada, segunda disminuida o el famoso tritono? yo creo que hay dos factores involucrados, uno es lo diminuto de la diferencia, que es casi imperceptible para un oído humano, y otro es la cultura, ya que el temperamento igual se usa desde fines del barroco, así que estamos culturalmente acostumbrados a que los instrumentos estén ligeramente "desafinados"
Buen luego de toda esta perorata ¿qué opinión me merece el la a 432?
honestamente ninguna, siempre me ha parecido que afinar el la a 440Hz es una mera arbitrariedad, y que lo establezca un estándar ISO no le quita su carácter arbitrario. Cada cual pueda afinar el la a la frecuencia que le plazca pero que no se queje si no puede acoplarse a ninguna banda/orquesta.
A propósito, yo siempre me he preguntado qué pasa con todos los pueblos que desarrollaron sistemas musicales melódicos o armónicos aparte de los europeos. Tenemos algo de información sobre las escalas arábicas y orientales, pero qué hay de la música africana, o la música inca (¿qué relación existía entre sus tonos y semitonos?, ¿a qué frecuencia afinaban el la?, y tantas otras preguntas que me vienen a la cabeza)