¿Cuantos subs de 131 dbs necesito para llegar a 141dbs?

javilozal escribió:

es mejor tener 3 subs de 131dbs sacandote 141 dbs, que un solo sub de 141dbs. Cierto no?

Depende de lo que uno considere "mejor". Yo no me arrimaría a una fuente de sonido de 131 dB ni loco, y me fastidiaría bastante que hubiese una a menos de 1 km de donde vivo, pero cada uno tiene sus vicios.

#31

No entiendo lo que quieres decir...

Que personalmente no me gusta la música alta, los entornos ruidosos ni estar expuesto a niveles de presión acústica que provoquen patologías en el oído, así que conseguir esa potencia para mí no es un triunfo de la tecnología, sino un riesgo para la salud.

Hola,

Veo varios "cabos sueltos" en este hilo, aunque las respuestas correctas están ahí.

Una de las explicaciones que faltan está en la siguiente propiedad del logaritmo:

Alguien escribió:

El logaritmo de una potencia es igual al exponente multiplicado por el logaritmo de la base.

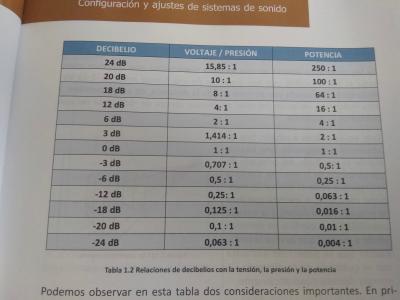
Como ya se ha comentado, la relación entre voltaje y potencia es como sigue: potencia igual al cuadrado del voltaje partido de la impedancia. Esta relación es similar entre la potencia acústica y la presión sonora.

Cuando hablamos de presión o voltaje, el coeficiente del logaritmo pasa a ser 20 en lugar de 10 para calcular la relación en dB entre la referencia y el valor a calcular. Siendo esto así, 20*log(2) = 6 dB en lugar de 10*log(2) = 3 dB.

Por tanto, el doble de presión sonora (de fuentes coherentes, medido desde un punto equidistante a ambas) se cuantifica como un incremento de 6 dB SPL en lugar de 3. Ésto (doblar la presión) implica cuadriplicar la potencia (acústica).

La otra confusión parece venir del caso en el que ponemos dos altavoces "de 10W" juntos.

En ese caso, no estamos cuadruplicando la potencia (que aquí sería eléctrica disipada, o más bien máxima potencia eléctrica que el altavoz soporta antes de sufrir daños, aunque esto es otro tema). Lo que tenemos es dos fuentes coherentes, con un nivel de X dB SPL cada una. Si medimos desde un punto equidistante a ambas, la suma será de X + 6 dB SPL. La potencia eléctrica es irrelevante para este cálculo.

En un escenario ideal, con un amplificador ideal, si ponemos una segunda caja de Y Ohm en paralelo a la primera (suponiendo que la potencia disipada sea de 10W) el voltaje se mantendría, pero la corriente eléctrica suministrada por el amplificador se duplicaría, al pasar la impedancia a ser la mitad, pasando el sistema de altavoces a disipar el doble de potencia (20W).

Si la potencia se duplica, lo lógico sería pensar que el SPL aumentará en 3 dB, pero esa relación es errónea. La relación entre la potencia entregada por el amplificador (y disipada en los altavoces en forma de calor o sonido) y el nivel de presión sonora viene determinada por la sensibilidad de éstos. Cada uno se comportará como una fuente sonora de Z dB SPL a 1W, 1m, y X dB SPL con 10 W. Mediremos X + 6 dB SPL en un punto equidistante a ambos.

Espero no haber liado más la cuestión y no haberme hecho un lío con los números.

Un saludo.

Hola
. Anteriormente he volcado lo que he leido. Que el doble de superficie provoca el doble de presion y con ello 6 dB SPL, etc. Sin embargo, debo confesar de que no me convence en absoluto, y no soy tecnico, ni cientifico, ni tengo instrumentos de medicion. A pesar de que he encontrado lo que mencione en varios sitios muy respetables , no me convence el hecho de que duplicar la potencia electrica, cuadruplique la potencia acustica. La energia, y con ello la potencia, no puede ser creada ni destruida, solo tranformada.
Lo que no me queda claro, es por que se supone que usar 2 altavoces , por mas coherentes que sean, signifique duplicar la presion lograda. En principio, justamente, la presion lograda deberia depender del cuadrado de la energia aplicada, o de la potencia en ese caso
He aprendido que duplicar la potencia electrica al parlante, implica ganar 3 dB SPL . Logicamente, 3 es abreviadamente 10 multiplicado por 0,30103, que es el logaritmo decimal de 2, lo cual es totalmente coherente con definir SPL como watt / metro cuadrado, cuando esa energia es irradiada en un espacio tridimensional
Evidentemente, si SPL se define como cuadrado de la presion, y lineal con potencia, la potencia esta ligada al cuadrado de la presion.
Pero sigo sin entender, porque duplicar el area radiante, significa duplicar la presion. Humildemente, imagino que justamente aumentar el area, implica mas exigencia de parte de la fuerza, o sea mas fuerza, o menos recorrido. En todo caso, determinada potencia, determinara otra determinada presion
Tengo la esperanza que alguien pueda aclarar mis dudas
Gracias

#35

La energía no se crea ni de destruye, en este caso se distribuye.

Hablamos de un punto en el espacio equidistante a ambas fuentes, en el que la suma es la máxima posible al haber coherencia tanto de amplitud como de fase, para todas las frecuencias.

Para que esto ocurra, hay otros puntos en los que hay una cancelación, cuya energía es 0, para una frecuencia en concreto. Otras se verán atenuadas en menor medida

La energía relativa a la interacción entre dos fuentes coherentes en cada punto del espacio depende de la distancia entre cada uno de esos puntos y ambas fuentes, es decir, de su relación de fase (ya que asumimos misma amplitud también) para una frecuencia determinada.

pedro escribió:

Logicamente, 3 es abreviadamente 10 multiplicado por 0,30103, que es el logaritmo decimal de 2, lo cual es totalmente coherente con definir SPL como watt / metro cuadrado, cuando esa energia es irradiada en un espacio tridimensional
Evidentemente, si SPL se define como cuadrado de la presion, y lineal con potencia, la potencia esta ligada al cuadrado de la presion.

El SPL no se define como Watt/m2, eso sería la unidad para la intensidad acústica. Y no, el SPL no se define como el cuadrado de presión. La P significa presión en esas siglas (Sound Pressure Level).

Quizá nadie sea capaz de explicártelo porque mezclas conceptos.

Un saludo

madre mia cada 3 meses el mismo post, menuda tenéis liada....

No se debería de poder contestar sin que se hubiera leído lo de siempre..suma de fuentes coherentes o incoherentes?, suma con una diferencia de fase 0º o no?...relación de potencia respecto a db?, que implica duplicar la potencia?, q es la ley cuadratica inversa y en q se diferencia de todo esto?...

Esto es lo mas Básico de nuestro mundo...debería(el moderador) de pasarlo a PA iniciación, por la reiteración del mismo post cada tres meses y por que no es normal q siempre se conteste lo mismo (no nos lleva a nada un post errático contestado de esta manera), generando las mismas dudas. ...(parecemos gente hablando sobre si la tierra es redonda o sobre si se puede viajar a la Luna...cuando ya se saben de sobra las respuestas y están mas que probadas..abstenerse los escépticos jajaja)

Señores/as esto es física y matemáticas, no puede existir ni la menor duda sobre como se calcula, no puede existir el yo creo q aunque ni me he puesto a calcularlo, la materia se reparte, energía, blablas varios....que yo recuerde hay varias formas de demostrarlo (+6dB) por medio de la formula de 20Log 2/1=Máx +6db..y por medio de la relación que existe en duplicar la potencia, ya esta.

#37
Que se haya tratado mucho sobre todo esto en Hispasonic no lo dudo, pero no es tan fácil y rápido encontrar la información exacta que uno necesita rebuscando en los hilos, ya sea porque hay mucha paja, porque hay opiniones diferentes, o porque la información clave está en un hilo cuyo título no describe específicamente lo que uno busca.
En mi opinión, es más útil buscar en artículos, o al menos es lo que suelo hacer yo antes de abrir un hilo. El problema en este caso, bajo mi propia experiencia, es que hay mucho artículo que confunde. Yo mismo ya he explicado que he leído montones de veces lo de que 2 fuentes sonoras iguales daban un aumento de +3 dB. Tras este debate de ahora ya tengo más claro que eso era un caso muy particular, y que la cosa no es tan sencilla, pero estoy seguro que dentro de un tiempo volverá a surgir un hilo similar.
La solución a este tipo de temas recurrente sería recopilar toda la información en un artículo que lo dejase claro de una vez por todas. Pero no sé si en Hispasonic hacen estas cosas. Hay un artículo relacionado con esto, que ya puse enlazado en uno de mis mensajes, pero quizás era demasiado técnico para los menos entendidos.

#38 en el libro de pepe esta perfectamente explicado. Las opiniones, las hay como los culos, pero la fisica es una y es la que es.

Alguien podría aclararme si es cierto q se necesitan 3 subs de 131 dbs para llegar a 141?

#40 La que te hemos terminado liando

3 subs de 131dbspl sumaran como máximo 140dbspl en un punto equidistante entre los tres perfectamente enfasados a 1 metro de los 3 ... ya para acabar de liara

Gracias Inxu!!!

javilozal escribió:

Alguien podría aclararme si es cierto q se necesitan 3 subs de 131 dbs para llegar a 141?

Eso, apiádense y háganle los deberes al muchacho; que le ha quedado PA para septiembre.

#43

Es que se ha desviado mucho el tema...aunque el saber no ocupa lugar.

He desempolvado mi viejo libro de fisica de la universidad, Sears Zemansky traducido al espaniol en Madrid. (perdon por la enie, no encuentro forma de que este teclado la escriba),
Alli se define a la intensidad de sonido, como la energia que pasa por una superficie determinada y perpendicular a la direccion de propagacion, y en un lapso de tiempo. Es decir, watt / metro cuadrado. Y sin hacer referencia a SPL, da la relacion logaritmica entre el menor sonido audible y la intensidad que se oye en dB, pero no especifica SPL, ni dBV ni nada. Y da una referencia de que el maximo sonido soportable, es de unos 120 dB, y el umbral de audicion, se ubica en 0 dB, bastante coherente con los dB SPL. Por otro lado, en internet, he visto que se refieren a SPL como intensidad de sonido, y en varios sitios.
Entonces, si es cierto que dB SPL se refieren a intensidad de sonido, nos encontramos con que duplicar cajas, interfieren entre si, sea constructivamente o destructivamente. Suponiendo constructivamente en forma ideal, se suman coherentemente las ondas, pero no se puede obtener mas potencia de la que se inyecta, 2 cajas con la misma potencia, duplican la potencia suministrada, y no pueden cuadruplicar la potencia emitida O sea, deberian aumentar el SPL en 3 dB y no en 6
Agradeceria una respuesta fundamentada y no un insulto soberbio sin explicacion He vertido la base de la duda con argumentos, y si pregunto es por una inquietud genuina
Saludos