No se si este error marcara alguna diferencia en el master

Nethox escribió:

El cálculo en coma flotante puede o no tener error de redondeo según la estabilidad de los algoritmos

Ya lo dije, el ejemplo que di tiene trampa, se que si esa prueba se hace en otro DAW es probable que no se obtenga el mismo resultado , pero es que simplemente yo le respondo a maximiliano respecto a si estoy equivocado o no

harpocrates escribió:

Por que hablas de Dither? tu exportas una mezcla para llevar a masterizar con dither? a mi por lo menos no se me ocurriría ya que no es el formato final, falta una etapa y la idea es llegar con la mezcla integra a ese proceso, por lo tanto exportaría a la máxima tasa de bits disponible, yo doy eso como algo de sentido común por lo que no me planteo el caso que tu señalas.

Ni yo, los casos que planteé eran para Jafer y el resto del foro.
Lo que es de sentido común es que otras personas desconocen estas cuestiones, o no existiría este hilo.

¿Y en serio me preguntas qué uso como formato intermedio?
Post #2 y #6 de este mismo hilo:

Nethox escribió:

Es una de las razones por las que recomiendo usar como formato intermedio 32 o 64 bits en coma flotante (a lo que trabaje tu DAW concreto)

Nethox escribió:

Formato intermedio (mezcla y master): 32 o 64 bits en coma flotante

Post del hilo de 2010-07 enlazado antes:

Nethox escribió:

Exportar al mismo formato interno del DAW, 32 ó 64 b fp (floating point, coma flotante). No hay formato intermedio con mayor calidad que el interno, sin compromiso.

Repetir en un medio escrito es absurdo y una pérdida de tiempo. Mejora tu lectura comprensiva y/o atención.

------------------------------------------------------------

harpocrates escribió:

El null test está hecho con la suma hecha en el motor a 64 bits flotantes y exportado a 24 bits sin dither.

harpocrates escribió:

Ya lo dije, el ejemplo que di tiene trampa, se que si esa prueba se hace en otro DAW es probable que no se obtenga el mismo resultado

Bien, si lo que dije para Jafer (y resto del foro) es aplicable o no a tu null test trivial, lo sabrás tú que lo has hecho, ya que no das suficientes explicaciones para validarlo científicamente. Pero es otro tema, y yo lo dejaría para el hilo de sumadores analógicos:
https://www.hispasonic.com/foros/he-realizado-summing-digital-8-canales/449247

------------------------------------------------------------

harpocrates escribió:

Nethox escribió:

Por cierto, lo anterior también refuta lo de que el DAW no tiene ruido. El cálculo en coma flotante puede o no tener error de redondeo según la estabilidad de los algoritmos, el valor de los operandos concretos, la precisión de los formatos iniciales e intermedios, el modo de la FPU x87 o uso de instrucciones SSE2, FMA y FMAC, números desnormalizados, etc.
Pero en general el mínimo error garantizado de una operación es 0.5 ULP, a lo cual se llama "correctly rounded". Algunas garantizan 1 o 2 ULP. Y otros algoritmos pueden perder la significación completa (la suma "ingenua" entre ellas), tener desbordamiento y dar resultados extraños. Es un tema complejo, el campo de las matemáticas llamado análisis numérico se dedica a su estudio.

No será distorsión? a ver esta bien que le llamemos ruido de cuantizacion y ese tipo de cosas, pero lo que es en realidad es distorsión de la señal original, que en el caso de la prueba que hizo daniel la distorsión producto de errores en la recuantizacion de las muestras es tal que es claramente audible, pero tu de lo que estas hablando es de relación señal/ruido, como aplica la relación señal ruido en esto? no me mezcles los conceptos que lo que he dicho es correcto, no así lo que tu estas planteando ahora.

Esto es el colmo, tú eres el que mezcla conceptos (mis 2 casos condicionales iniciales) y no se entera (formato intermedio que recomiendo y ahora el SNR).
Y no concretas qué es supuestamente incorrecto, ni por qué.

Desde el principio hablé de 3 fuentes de ruido: error o distorsión de cuantización, ruido de fondo del convertidor AD/DA, dither. maximilianofv parece que lo entendió en su post #8 .
Tras tu respuesta, amplié el error de cuantización con la pérdida de significancia algorítmica y sus múltiples variables.

Ciertamente es error o distorsión de cuantización pero, cuando se modela matemáticamente, se suele llamar ruido de cuantización. Es un término correcto que no me he inventado yo:
https://en.wikipedia.org/wiki/Quantization_%28signal_processing%29#Quantization_noise_model
https://en.wikipedia.org/wiki/Signal-to-quantization-noise_ratio

Se aplica tanto a conversión AD/DA como a error de redondeo acumulado en DSP (round-off):
http://www.dspguide.com/ch4/4.htm
https://en.wikipedia.org/wiki/Round-off_error

Wikipedia ENG: round-off error escribió:

A round-off error, also called rounding error, is the difference between the calculated approximation of a number and its exact mathematical value. [...] This is a form of quantization error.

De hecho, la conversión AD/DA es un buen ejemplo de por qué se consolida todo en el término ruido: no sólo tiene error de cuantización, sino jitter, ruido de Johnson-Nyquist, EMI interno, y quizá más tipos. Todo se suma en un valor de dB SNR, normalmente con ponderación A para maquillar especificaciones técnicas .

De la teoría anterior salen estas fórmulas, en escala logarítmica (dB):
SQNR = 20 * log10(2^p) ≈ 6.02 * p
Donde p es el número de bits de cuantización, es decir, la precisión/mantisa del formato, sea entero o en coma flotante.
Sin embargo, el rango dinámico (DR) de los formatos en coma flotante es muy superior gracias al escalado del exponente (resolución variable):
DR ≈ 6.02 * 2^e
https://en.wikipedia.org/wiki/Signal-to-noise_ratio#Digital_signals

Por tanto, todo lo que reduzca la significancia de la precisión/mantisa es ruido que reduce el SNR. Basta con sustituír el nuevo valor de p efectiva en la fórmula. Normalmente se empieza a perder por los bits menos significativos (LSB).
A un DAW le pueden afectar 2 de las 3 fuentes anteriores, según el diseño y tu flujo de trabajo: el error de cuantización y el dither. Obviamente el del convertidor AD/DA no.

harpocrates escribió:

El exportar a 32 o 64 bits flotantes en lugar de 24 no hace absolutamente ninguna diferencia respecto a la relación señal ruido.

Cierto para el caso de 24 bits enteros y 32 bits en coma flotante, que tienen precisión 24:
SNR = 20 * log10(2^24) = 144.49 dB
Falso para el caso de 64 bits en coma flotante, que tiene precisión 53:
SNR = 20 * log10(2^53) = 319.09 dB

harpocrates escribió:

Si tu exportas usando en motor de audio del DAW, no se agregará ningún ruido adicional, ya que el renderizado es un calculo matemático

Tienes seguro el error de cuantización del formato de salida seleccionado, más un posible error de redondeo acumulado y pérdida de significancia algorítmica de todos los plugins y summing.
Y un posible dither, a veces no desactivable por el usuario.

Yo recomendaría leer atentamente al compañero Nethox, para mí es un crack a nivel técnico y he aprendido cosas interesantes gracias a él. Un saludo!!

Sólo por curiosidad, me he dedicado a hacer la misma prueba que hizo el compañero harpocrates en el post #9 usando Cubase 5. Si bien en el medidor del canal MASTER no se aprecia señal al hacer el "null test", si usamos algo como el Voxengo SPAN podemos apreciar claramente el error en cada caso. He hecho lo mismo, exportar con el fader master a 0dB primero y a -6dB después. Aclaro también que la mezcla estaba a -20dB RMS, con lo que con material algo más apretado el error subiría un poco más. He exportado primero a 32 bit en coma flotante, luego a 24 enteros y luego a 16 (ya que estaba puesto...). El medidor del master no marca nada en ningún momento porque el nivel del error se queda en todos los casos por debajo de 100dBFS (creo que Cubase 5 empieza a marcar "algo" a partir de unos -96dBFS, no sé si en Reaper o en otros funciona igual la cosa).

Lo dicho, adjunto las capturas a 32bit float, 24bit y 16bit respectivamente. Me sorprendió ver "algo" en la prueba a 32bit float, pero supongo que nada es absolutamente "limpio". Probablemente, a 64bit float el error ya no se vería (aunque no tengo forma de comprobarlo ya que uso la versión de 32 bits).

harpocrates escribió:

harpocrates escribió:
El exportar a 32 o 64 bits flotantes en lugar de 24 no hace absolutamente ninguna diferencia respecto a la relación señal ruido.
Cierto para el caso de 24 bits enteros y 32 bits en coma flotante, que tienen precisión 24:
SNR = 20 * log10(2^24) = 144.49 dB
Falso para el caso de 64 bits en coma flotante, que tiene precisión 53:
SNR = 20 * log10(2^53) = 319.09 dB

Nethox, la humildad no es pecado, de hecho se considera virtud, no le tengas miedo, estas equivocado, no me lo achaques a mi con eso de que soy un bruto y no tengo comprensión lectora y asume el error que estas cometiendo, no estoy diciendo que no sepas, simplemente esas interpretando mal la información es de caballeros no decir cosas como esta:

Nethox escribió:

Repetir en un medio escrito es absurdo y una pérdida de tiempo. Mejora tu lectura comprensiva y/o atención.

por que el que no sigue el hilo de esto eres tu en realdiad:

El ruido se encuentra en las etapas "FISICAS", cuando tu grabas, tu piso de ruido está determinado por el piso de ruido del convertidor A/D, si tu exportas a 64 bits flotantes, donde estará el ruido? a -320 dB? no, estará mucho mas arriba donde estaba el piso de ruido del convertidor al momento de grabar, de hecho aun mas arriba debido al ruido del previo, esa es tu relación señal ruido que no es lo mismo que el rango dinámico de tu secuenciador, ese calculo que estas haciendo es para el rango dinámico, pero si vienes con cosas grabadas no es lo mismo rango dinámico que SNR.

Luego mezclas y dentro del secuenciador tienes un rango dinámico mayor, obvio, pero y acá está tu error, tu sales por un convertidor D/A a 24 bits, si exportas a 64 bits, es cierto, todo valor que haya superado los 0 dBfs en el master no se verá afectado, quedará correctamente guardado en el archivo, pero si tu lo conviertes en audio es diferente, el valor numérico si bien puede ser expresado dentro de ese archivo, al ser convertido a una señal generará clipping en el convertidor, por que el archivo tiene guardado valores que superan lo que el convertidor es capaz de representar, entonces no estas yendo a lo practico. Tu al importar esa pista con esos valores te va a tocar bajar luego el fader, no es gran cosa, no cuesta nada bajar el fader, pero permiteme señalarte que te estas quedando en la teoría y no estas viendo como funciona esto en la practica.

Yendo al caso de bajar el fader del master, supongamos que tu ruido estaba a -96 dB y tu señal tiene un RMS de -10 dB, es decir 86 dB de relación señal/ruido y bajas el fader tanto que el ruido queda fuera del rango dinámico de los 24 bits, pero sin aun afectar a la señal propiamente tal, que pasa? teóricamente tu piso de ruido ahora está mas cerca de tu señal, pero para efectos prácticos si exportas a un archivo, el DAW no te agregará ruido físico, ruido real, solamente tendrás menos rango dinámico en ese archivo, pero si ese archivo lo importas en un proyecto el piso de ruido no habrá subido, por que no era ruido real, simplemente es el rango dinámico que te da dicha codificación, entonces al subir el fader na habrás ganado ruido, y el rango dinámico seguirá siendo el que te de el motor de audio, por que digitalmente no hay ruido en este ejercicio particular, no estamos hablando de mezclar, mover fader y esas cosas, simplemente de exportar, tu SNR no se habrá disminuido a no ser que pases por una etapa física, si exportas desde una salida fisica, por ejemplo hacia un sumador, si, tu señal estará mas cerca del ruido efectivamente habrás perdido SNR y ahí es donde llegamos al ruido de cuantizacion.

Es lo mismo hablar de relación señal/ruido que hablar de ruido de cuantizacion? para este caso? para lo que estamos hablando? analizalo y me respondes con coherencia por favor, por que paciencia tengo, pero no cuando me insultan, he seguido a la perfección todo lo que dices, el enredado eres tu, asúmelo como caballero.

harpocrates escribió:

Tienes seguro el error de cuantización del formato de salida seleccionado, más un posible error de redondeo acumulado y pérdida de significancia algorítmica de todos los plugins y summing.

Reitero, ese ruido es una modificación, o distorsión de la señal, no tiene que ver con el ruido de la relación señal/ruido, a mi no me lo expliques eso, date cuenta de la secuencia que llevamos, tu hablaste de relación señal/ruido, confundiendola con rango dinamico, y confundiendo el ruido de cuantizacion con el piso de ruido que es lo que se considera para la SNR, que viene de las etapas físicas, ese ruido no te lo aumenta el secuenciador, si tu me mezclas lo de la SNR con el ruido de cuantizacion, pues obviamente que esta conversación se vuelve incomprensible si no es de lo que estamos hablando pues hombre.

Nethox escribió:

¿Y en serio me preguntas qué uso como formato intermedio?

No, no te lo he preguntado, mas bien fue esta mi pregunta:

Nethox escribió:

Por que hablas de Dither? tu exportas una mezcla para llevar a masterizar con dither?

Eso se llama pregunta capciosa, cuya finalidad es dejar en evidencia el error, no hace falta responderla, simplemente es para lograr que te sonrojes. Si me estas diciendo que exportas a 64 bits flotantes, por que me hablas de dither, esta discusión se genera por que precisamente por eso, por que me cuestionas con planteamientos a los que no me he referido.

Daniel Lazarus escribió:

Yo recomendaría leer atentamente al compañero Nethox, para mí es un crack a nivel técnico y he aprendido cosas interesantes gracias a él

No lo dudo, pero analiza bien lo que estamos discutiendo, Nethox está nublado estos días o ha querido sacarse una discusión de la nada, no se, pero no soy yo el que armé este enredo.

#18

Efectivamente, acabo de corroborarlo, no son exactamente iguales, este es el momento para comenzar a correr en círculos muchachos

Me entro la curiosidad respecto a que pasa si el sumador es a punto fijo, haré la prueba.

harpocrates escribió:

Me entro la curiosidad respecto a que pasa si el sumador es a punto fijo, haré la prueba.

Hecho, ahora si se anulan completamente

[ Imagen no disponible ]

Además que se les paso un detalle los plugins principalmente los compresores fueron calibrados en la mescla para filtrar cierto nivel de señal, al bajar el master el calibrado deja de tener efecto, ya que cambia la potencia de la señal en todos los tracks.

Desde luego es una discusión interesantísima. Os leo con atención.
Me gustaría tener tiempo para hacer también estas pruebas en coma flotante y a punto fijo...
Lo que sí que tengo claro (creo) es que la relación S/N queda fuera del debate, como dice Harpocrates, al ser una medida relacionada con las etapas analógicas y los convertidores.

#22 Raul, estás seguro de esto que dices? Tal vez no he comprendido bien el mensaje, pero hasta dónde yo se el volumen del master es un parámetro relativo y no cambiará la relación de potencias en la mezcla, ni tampoco la potencia de la señal en ninguno de los tracks.

#22
Incorrecto, la ganancia del fader Master se aplica mucho después de los compresores insertados en cada canal, así que no afecta al ajuste de los umbrales.
Ni siquiera sucede con el fader de cada canal, salvo que insertes el compresor en modalidad "post-fader". Por defecto, las inserciones son "pre-fader" justamente para evitar trastocar el gain-staging de los plugins al mezclar.
Los envíos son al revés, por defecto "post-fader".
Ejemplo: al bajar un fader de canal, se evita que el umbral quede demasiado alto y casi no comprima, pero la reverberación sí baja para mantener la misma proporción respecto a la señal directa.

El flujo de señal de un DAW es muy lineal, aquí tienes unos diagramas útiles aunque no se vean muy bien:
http://www.soundonsound.com/sos/mar04/articles/cubasenotes.htm

Por cierto, potencia no es un término muy apropiado, es mejor "nivel" o "amplitud" de la señal.

Nethox escribió:

Es una de las razones por las que recomiendo usar como formato intermedio 32 o 64 bits en coma flotante [...] evitar fallo software, por ejemplo que se aplique dither sucesivas veces en vez de sólo una al final. Y con algoritmos que no sabes si acumulan error (noise shaping) o son inocuos (distribución de probabilidad rectangular o triangular, el habitual por suerte).

Incorrecto que el dither triangular sea inocuo en aplicaciones sucesivas, aunque sí sería menos dañino que el noise shaping.
Creo que reaplicar triangular generaría una función de densidad de probabilidad normal o gaussiana, pero con más amplitud de la mínima necesaria para evitar la distorsión de cuantización y su modulación.

Nethox escribió:

Incorrecto que el dither triangular sea inocuo en aplicaciones sucesivas, aunque sí sería menos dañino que el noise shaping. Creo que reaplicar triangular generaría una función de densidad de probabilidad normal o gaussiana, pero con más amplitud de la mínima necesaria para evitar la distorsión de cuantización y su modulación.

Alguien escribió:

PROBLEMILLA KIEN MAYUDA tengo traktor con audio8dj y tengo conectados dos technics y aora me he comprado un piooner 800 mk2 y no se como instalarlo atraves de mi tarjeta audio8dj como lo ago ? un saludo gracias

Las 2 Españas en

jajaja.... avalle, recoges unas perlas que no veas... míatú!

Perdón por el offtopic, pero es que hispasonic a veces me mata; esto de pasar del analfabetismo funcional típico del neo-plodustol a la tesis doctoral sobre DSP sin término medio, me tiene loco...

harpocrates escribió:

Luego mezclas y dentro del secuenciador tienes un rango dinámico mayor, obvio, pero y acá está tu error, tu sales por un convertidor D/A a 24 bits, si exportas a 64 bits, es cierto, todo valor que haya superado los 0 dBfs en el master no se verá afectado, quedará correctamente guardado en el archivo, pero si tu lo conviertes en audio es diferente, el valor numérico si bien puede ser expresado dentro de ese archivo, al ser convertido a una señal generará clipping en el convertidor

Ni siquiera he mencionado el clipping en mi anterior post, pero estamos de acuerdo y no hay error porque ya dije esto en 2010-07:

Nethox escribió:

La representación interna (64 b fp) supera por mucho a la externa (24 b), pero el 0 dB FS de ambas está sincronizado[5], así que ajustando la interna (fader Master) se evita el clipping en la externa (DAC/fichero).

Realmente el clipping no se genera en el convertidor DA sino en el DAW. O en el driver de la interfaz de audio como tarde, pues los hay que aceptan y convierten formatos de 32/64 bits flotantes a 16/24 enteros (p. ej. ALSA).

----------------------------------------

harpocrates escribió:

El ruido se encuentra en las etapas "FISICAS", cuando tu grabas, tu piso de ruido está determinado por el piso de ruido del convertidor A/D, si tu exportas a 64 bits flotantes, donde estará el ruido? a -320 dB? no, estará mucho mas arriba donde estaba el piso de ruido del convertidor al momento de grabar, de hecho aun mas arriba debido al ruido del previo, esa es tu relación señal ruido

Pareces no darte cuenta de que, desde el último párrafo del post #14 y todo el #17 , yo no he estado tratando el tema original, sino refutando tus siguientes generalizaciones falsas de ruido y SNR, en esos mismos términos generales:
1) "el DAW no tiene ruido"
2) "El exportar a 32 o 64 bits flotantes en lugar de 24 no hace absolutamente ninguna diferencia respecto a la relación señal ruido"
3) "Si tu exportas usando en motor de audio del DAW, no se agregará ningún ruido adicional, ya que el renderizado es un calculo matemático"

Es una cuestión de rigor y evitar desinformación, no sólo de conocimientos.
Una generalización falsa es dañina aun estando dentro de un hilo concreto: a mordus le has medio-convencido erróneamente en #23 de que la SNR sólo existe en "etapas analógicas y convertidores".

Por el principio de falsabilidad, con un solo contraejemplo me bastaba para refutarte:
1) El DAW tiene muchos ruidos digitales. Añado a los ya dichos: clics y pops por desincronía y buffers, aliasing en SRC, pre y post-echos en ecualizadores.
2) El formato determina la SQNR máxima.
En los clips de audio y capturas adjuntas "sine 997Hz -20dBFS int{24,8}b dither.wav" se ve y oye la disminución de SNR (90+ dB) por reducir la precisión de 24 a 8 bits enteros.
También se puede ver y oír el ruido de cuantización aislado en el clip diferencial "sine 997Hz -20dBFS diff pre-dither.wav".
3) El ruido no es exclusivo del dominio analógico o físico, también existe en dominio digital. Dices que es un cálculo matemático, sí, pero con precisión limitada para un conjunto infinito de números reales.
Toda señal no deseada es ruido y computa en la SNR. Dile a los que hacen Noise o Glitch music ITB que no existe ruido digital.

harpocrates escribió:

esa es tu relación señal ruido que no es lo mismo que el rango dinámico de tu secuenciador, ese calculo que estas haciendo es para el rango dinámico, pero si vienes con cosas grabadas no es lo mismo rango dinámico que SNR.

Incorrecto parcialmente. El cálculo es para la SQNR máxima, que sólo es equiparable al rango dinámico (DR) para formatos enteros, no en coma flotante como el que planteas de 64 bits.

Para enteros, se cumple DR = SQNR máxima. Luego está la SNR, que es <= SQNR (o DR). Hay 2 valores.
Para coma flotante, el DR sólo depende del exponente, y la SQNR máxima sólo depende de la precisión/mantisa. Dejan de ser iguales. Luego está la SNR, que sigue siendo <= SQNR máxima. Hay 3 valores.

Lógicamente, la mayor fuente de ruido digital o analógico es la que determina la SNR efectiva. Y se parte desde la SQNR máxima del formato:

Nethox escribió:

todo lo que reduzca la significancia de la precisión/mantisa es ruido que reduce el SNR. Basta con sustituír el nuevo valor de p efectiva en la fórmula

Creí que usar negrita y oblícua, los adjetivos "nuevo" y "efectiva", y la referencia a Wikipedia que decía "theoretical maximum SNR" sería suficiente claridad.

No calculé el DR por ser irrelevante en formatos de coma flotante. Pero aquí está por completitud, seguido de un esquema de fórmulas:
DR(binary32) = 1541.27 dB
DR(binary64) = 12330.19 dB
Excluyendo los números desnormalizados, el rango es ligeramente menor:
DRnorm(binary32) = [ -758.60, 770.64] = 1529.23 dB
DRnorm(binary64) = [-6153.05, 6165.09] = 12318.15 dB
https://en.wikipedia.org/wiki/Normal_number_%28computing%29

Enteros:
DR = SQNR máxima = 6.02 * p
SNR <= (SQNR máxima = DR)
Coma flotante:
DR = 6.02 * 2^e
SQNR máxima = 6.02 * p
SNR <= SQNR máxima

----------------------------------------

harpocrates escribió:

Yendo al caso de bajar el fader del master, supongamos que tu ruido estaba a -96 dB y tu señal tiene un RMS de -10 dB, es decir 86 dB de relación señal/ruido y bajas el fader tanto que el ruido queda fuera del rango dinámico de los 24 bits, pero sin aun afectar a la señal propiamente tal, que pasa? teóricamente tu piso de ruido ahora está mas cerca de tu señal, pero para efectos prácticos si exportas a un archivo, el DAW no te agregará ruido físico, ruido real, solamente tendrás menos rango dinámico en ese archivo, pero si ese archivo lo importas en un proyecto el piso de ruido no habrá subido, por que no era ruido real, simplemente es el rango dinámico que te da dicha codificación, entonces al subir el fader na habrás ganado ruido, y el rango dinámico seguirá siendo el que te de el motor de audio, por que digitalmente no hay ruido en este ejercicio particular, no estamos hablando de mezclar, mover fader y esas cosas, simplemente de exportar, tu SNR no se habrá disminuido a no ser que pases por una etapa física, si exportas desde una salida fisica, por ejemplo hacia un sumador, si, tu señal estará mas cerca del ruido efectivamente habrás perdido SNR y ahí es donde llegamos al ruido de cuantizacion.

Es lo mismo hablar de relación señal/ruido que hablar de ruido de cuantizacion? para este caso? para lo que estamos hablando? analizalo y me respondes con coherencia por favor

Este ejemplo lo acabas de sacar (tú), no lo estábamos hablando (nosotros).
Bajar el fader Master y exportar a 24 bits enteros es el caso hipotético 1 que planteé al principio. Ahora veo un error: no tuve en cuenta que Jafer regrabó algunas tomas de voz, no todas, por lo que el fader bajó una mezcla que incluía seguro ruido de fondo de alguna grabación de voz.
No especificó las otras pistas de la mezcla, así que podía estar programada ITB sin ruido, descontando el dither o el de cuantización.
Pero con la certeza del ruido de fondo, lo más probable es que éste supusiera un footroom mayor que los 6 dB de reducción del fader, así que la SNR no llegaría a modificarse.

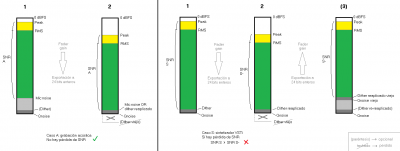
Adjunto un gráfico "Fader gain SNR 24b.png" donde se ven los dos subcasos: el A parte desde un clip con ruido añadido, el S no tiene ruido salvo el dither.
Puede ser necesario reaplicar dither al aplicar ganancia negativa.

Para el que quiera más detalles:
0) Los medidores de pico muestran el valor absoluto, tienen un tiempo de release y usan escala logarítmica. Los samples reales oscilan alrededor de 0, pueden cambiar instantáneamente (limitado por Fmuestreo) y usan escala lineal (en LPCM 16/24 típico).
1) La separación de señal limpia vs ruido es ficticia para su representación gráfica. Realmente en el valor de cada sample está todo sumado, incluído el ruido de cuantización y dither.
2) En los samples más próximos a 0 dBFS, simplemente el ruido es menor en términos relativos y lo tiene más difícil para alterar el paso de cuantización en que queda, pesará más la parte de señal.
3) La multiplicación del fader reduce linealmente el ruido y señal de todos los samples. Pero no el error de la recuantización posterior, porque en LPCM el paso de cuantización es uniforme. Por tanto, el error relativo de recuantización crece respecto a la señal (de ahí que Qnoise esté siempre fijo en la parte inferior de la barra).
Si hay suficiente footroom de ruido disponible, no importa. Si no hay suficiente, es fundamental usar dither (TPDF a 24b) para evitar que el error de recuantización correlado se acumule rápidamente hasta niveles audibles.
4) El dither habitualmente se suma a la señal, no reemplaza. Puede alterar ligeramente el nivel de Peak y RMS. Probablemente cause clipping si se aplica a una señal normalizada a 0 dBFS.
5) Tras multiplicar por ganancia < 1 y aplicar dither, los samples entre [-0.5, 0.5] se redondean a 0 y pierden. Igual que sucede en el clipping por los extremos.